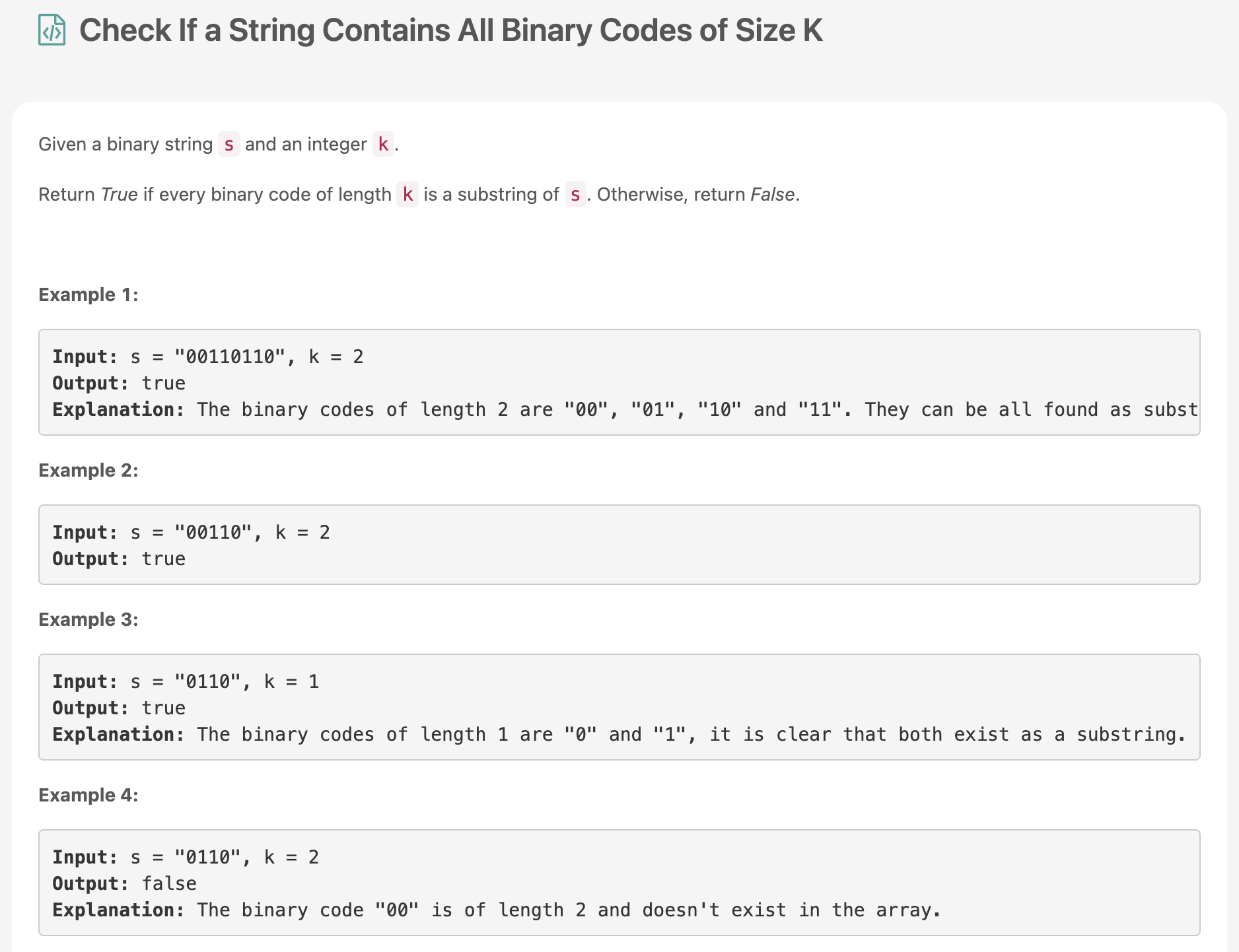
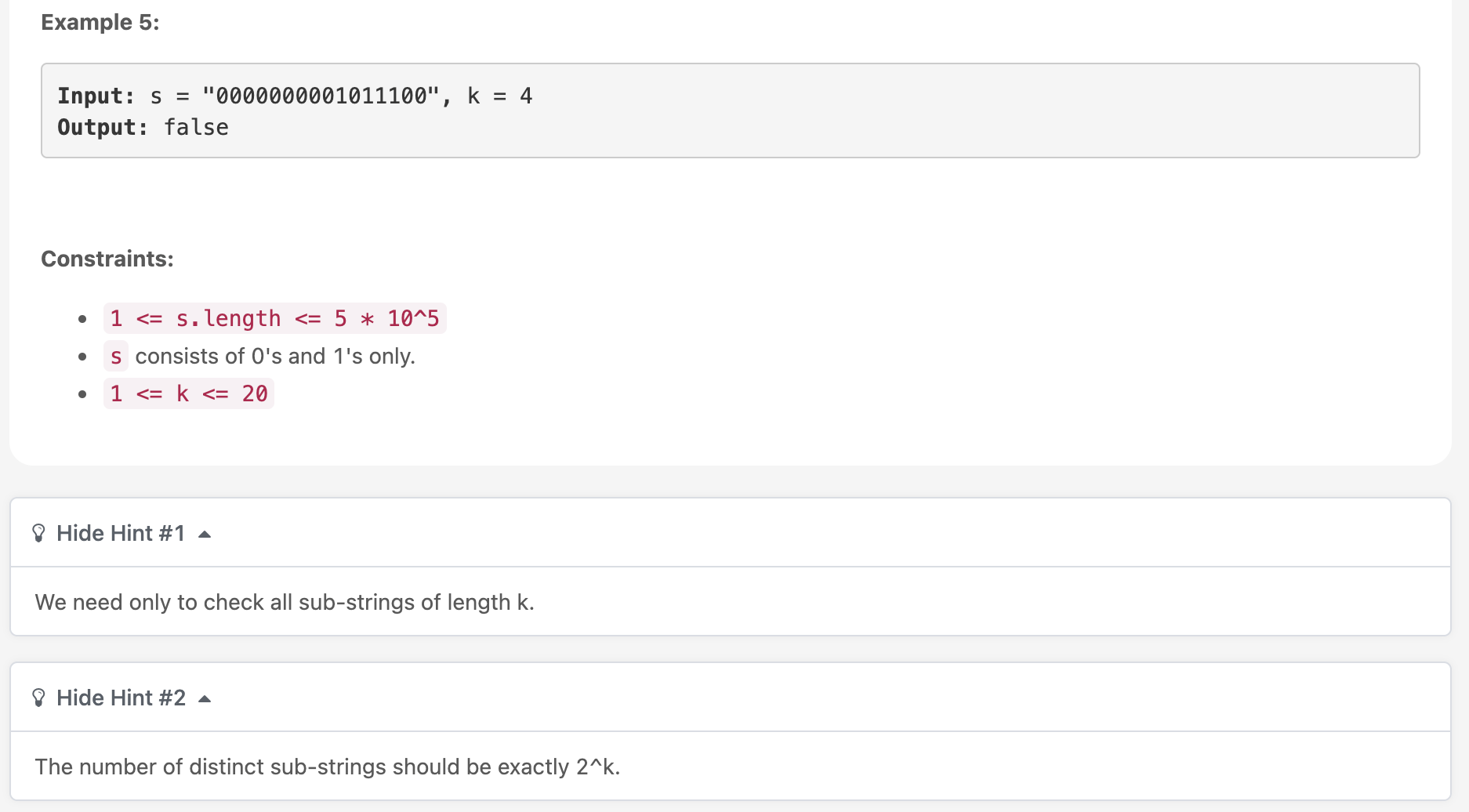
problem
code
1st try: failed time limit exceeded
class Solution {
List<String> list;
public boolean hasAllCodes(String s, int k) {
if (s.length() < k)
return false;
list = new ArrayList<>();
this.create(k, "", list);
for (int i = 0; i < list.size(); i++) {
// contains O(N)
// Boyer–Moore string-search algorithm
if (!s.contains(list.get(i)))
return false;
}
return true;
}
// 0, 1
// [00 01] [10 11]
// [000, 0001] [010, 011] [100, 101] [110 111]
// 2^N expoential time complexity
public void create(int k, String s, List<String> list) {
if (s.length() == k) {
list.add(s);
return;
}
create(k, s + "1", list);
create(k, s + "0", list);
}
}2nd try: check if the number of unique substrings equal to the number of binary cases length is K
class Solution {
public boolean hasAllCodes(String s, int k) {
// int need = Math.pow(2, k);
// brilliant!!!!
int need = 1 << k;
Set<String> set = new HashSet<>();
for (int i = k; i <= s.length(); i++) {
String sub = s.substring(i - k, i);
if (!set.contains(sub)) {
set.add(sub);
need--;
if (need == 0)
return true;
}
}
return false;
}
}Time: O(NK), N is the length of s, K is the cost of calculating substring
Space: O(2^K), there must be K
# python
class Solution:
def hasAllCodes(self, s: str, k: int) -> bool:
got = {s[i - k : i] for i in range(k, len(s) + 1)}
return len(got) == 1 << k3rd try: leetcode
