[leetcode] Coin Change

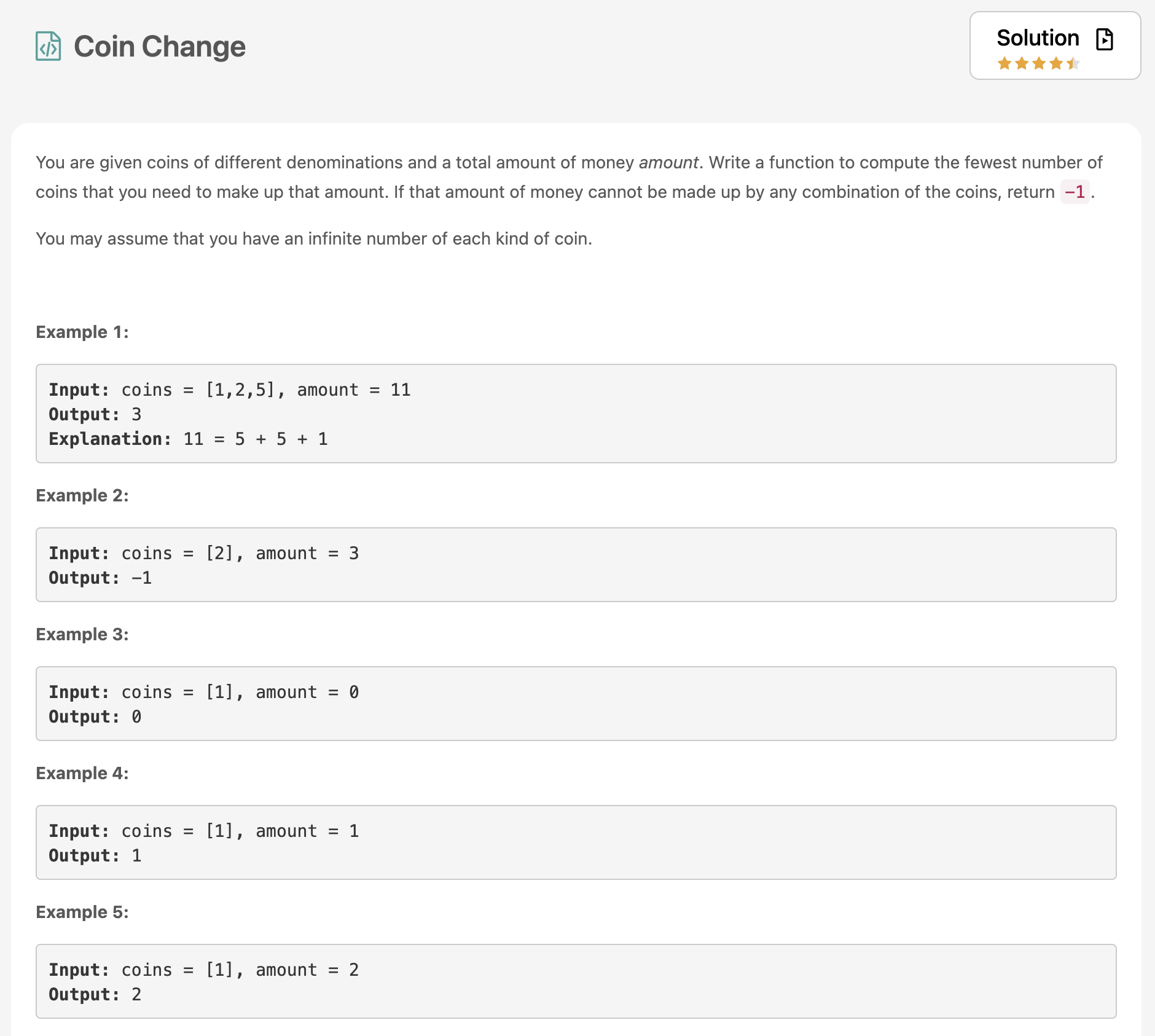
problem

code

1st try: failed,

[186,419,83,408]
6249

The idea was to divide the amounts in descending order of coins. But it does not work because there is a set of coins can divde the amounts although the order is not descending

class Solution {
    public int coinChange(int[] coins, int amount) {
        int len = coins.length;
        
        int share = 0;
        int rest = 0;
        int sum = 0;        
        Arrays.sort(coins);
        for (int i = 0, j = len - 1; i < j; i++, j--) {
            int temp = coins[i];
            coins[i] = coins[j];
            coins[j] = temp;
        }
        // System.out.println(coins.toString());
        Arrays.stream(coins).forEach(System.out::println);
        
        for (int i = 0; i < len; i++) {
            // System.out.println(coin);
            int coin = coins[i];
            share = amount / coin;
            rest = amount % coin;
            amount = amount - coin * share;
            System.out.println(" share:" + share + " rest:" + rest + " amount:" + amount);

            sum += share;
        }
        if (amount != 0) return -1;
        return sum;
    }
}

2nd try: Dynamic problem

[0, max, max, max, max, ..., max] where length is amount + 1
Each element represents the number of min case to be each index
max is just given value

[1, 2, 5] 8

i:1
coin:1 <= i:1 true => dp[1 - 1] != Integer.MAX_VALUE)
dp[1] = dp[1] vs 1 + dp[0] => 1
coin:2 <= i:1 false
coin:5 <= i:1 false
[0, 1, ...]

i:2
coin:1 <= i:2 true => dp[2 - 1] != Integer.MAX_VALUE
dp[2] = dp[2] vs 1 + dp[2 - 1] => 2
coin:2 <= i:2 true => dp[2 - 2] != Integer.MAX_VALUE
dp[2] = dp[2] vs 1 + dp[2 - 2] => 2 vs 1 + 0 => 1
coin:5 <= i:2 false
[0, 1, 2 => 1, ...]: there are 2 ways to be 2, [1, 1], [2]

i:3
coin:1 <= i:3 true => dp[3 - 1] != Integer.MAX_VALUE
dp[3] = dp[3] vs 1 + dp[3 - 1] => max vs 1 + 1 => 2
coin:2 <= i:3 true => dp[3 - 2] != Integer.MAX_VALUE
dp[3] = dp[3] vs 1 + dp[3 - 2] => 2 vs 1 + 1 => 2
coin:5 <= i:3 false
[0, 1, 2=>1, 2=>2, ...]
i:4
coin:1 <= i:4 true => dp[4 - 1] != Integer.MAX_VALUE
dp[4] = dp[4] vs 1 + dp[4 - 1] => max vs 1 + 2 => 3
coin:2 <= i:4 true => dp[4 - 2] != Integer.MAX_VALUE
dp[4] = dp[4] vs 1 + dp[4 - 2] => 3 vs 1 + 1 => 2
coin:5 <= i:4 false
[0, 1, 2=>1, 2=>2, 3=>2,...]
i:5
coin:1 <= i:5 true => dp[5 - 1] != Integer.MAX_VALUE
dp[5] = dp[5] vs 1 + dp[5 - 1] => max vs 1 + 2 => 3
coin:2 <= i:5 true => dp[5 - 2] != Integer.MAX_VALUE
dp[5] = dp[5] vs 1 + dp[5 - 2] => 3 vs 1 + 2 => 3
coin:5 <= i:5 true => dp[5 - 5] => Integer.MAX_VALUE
dp[5] = dp[5] vs 1 + dp[5 - 5] => 3 vs 1 + 0 => 1
[0, 1, 2=>1, 2=>2, 3=>2, 3=>3=>1]
i:6
coin:1 <= i:6 true => dp[6 - 1] != Integer.MAX_VALUE
dp[6] = dp[6] vs 1 + dp[6 - 1] => max vs 1 + 1 => 2
coin:2 <= i:6 true => dp[6 - 2] != Integer.MAX_VALUE
dp[6] = dp[6] vs 1 + dp[6 - 2] => 2 vs 1 + 2 => 2
coin:5 <= i:6 true => dp[6 - 5] => Integer.MAX_VALUE
dp[6] = dp[6] vs 1 + dp[6 - 5] => 2 vs 1 + 1 => 2
[0, 1, 2=>1, 2=>2, 3=>2, 3=>3=>1, 2]
i:7
coin:1 <= i:7 true => dp[7 - 1] != Integer.MAX_VALUE
dp[7] = dp[7] vs 1 + dp[7 - 1] => max vs 1 + 2 => 3
coin:2 <= i:7 true => dp[7 - 2] != Integer.MAX_VALUE
dp[5] = dp[7] vs 1 + dp[7 - 2] => 3 vs 1 + 1 => 2
coin:5 <= i:7 true => dp[7 - 5] => Integer.MAX_VALUE
dp[5] = dp[7] vs 1 + dp[7 - 5] => 2 vs 1 + 1 => 2
[0, 1, 2=>1, 2=>2, 3=>2, 3=>3=>1, 2, 2]
i:8
coin:1 <= i:8 true => dp[8 - 1] != Integer.MAX_VALUE
dp[8] = dp[8] vs 1 + dp[8 - 1] => max vs 1 + 2 => 3
coin:2 <= i:8 true => dp[8 - 2] != Integer.MAX_VALUE
dp[8] = dp[8] vs 1 + dp[8 - 2] => 3 vs 1 + 2 => 3
coin:5 <= i:8 true => dp[8 - 5] => Integer.MAX_VALUE
dp[8] = dp[8] vs 1 + dp[8 - 5] => 3 vs 1 + 2 => 3
[0, 1, 2=>1, 2=>2, 3=>2, 3=>3=>1, 2, 2, 3]

1. i: amount
2. start from amount 0 to amount given [0, ..., given]
3. find dp[amount] from min (dp[amount], 1 + dp[amount - coin])
   • with each coin in [x, y, z, ..., t]
4. 1 + dp[amount - coin]
   • we calculated dp[amount - coin] before and then 1 + means the minimum number of coin (always 1) to be dp[amount].

[0, 1, 2, 2, 2, ?, max, max, max]
amount:5
coin:1 =>
what is the min number of coins at amount 4:2
with coin 1, to be 5 we just need one coin 1
thus the min number of coinsis 2(dp[amount 5 - coin 1]) + 1(add coin 1)

class Solution {
  
    public int coinChange(int[] coins, int amount) 
    {
      	int[] dp = new int[amount+1];
        dp[0] = 0;
      	// Arrays.fill(dp, Integer.MAX_VALUE);
      	for (int i = 1; i <= amount; i++) 
        {
        	dp[i] = Integer.MAX_VALUE;
        }

        for (int i = 1; i <= amount; i++) 
        {
           for (int coin: coins) 
           {
              if (coin <= i && dp[i - coin] != Integer.MAX_VALUE) 
              {
                  dp[i] = Math.min(dp[i], 1 +  dp[i - coin]); 
              }
           } 
        } 
        return (dp[amount] == Integer.MAX_VALUE) ? -1 : dp[amount]; 
    }

}

from geeksforgeeks- Find minimum number of coins that make a given value