백준 12015번 바로가기

---

📌 LIS

백준 11053번 바로가기

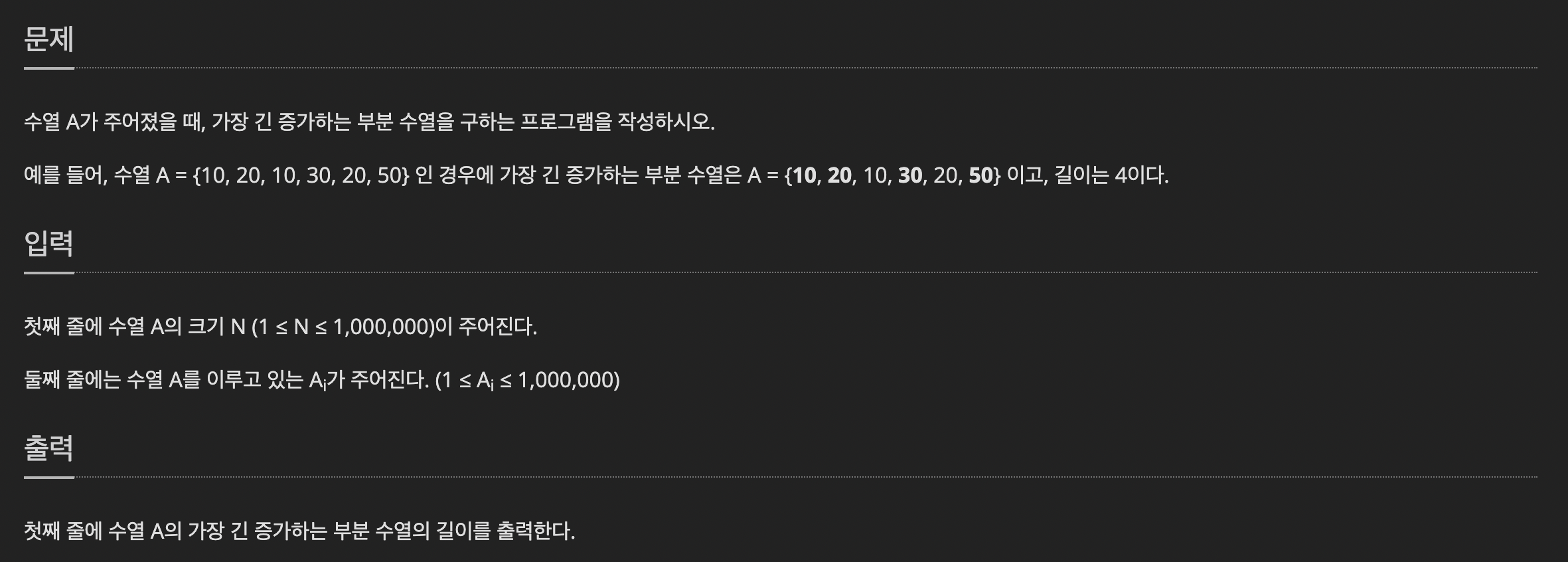
가장 긴 증가하는 부분수열에서 공부한 LIS를 더 효율적으로 구하는 문제이다.

import sys
input = sys.stdin.readline

n = int(input())

arr = list(map(int, input().split()))
length = [1 for i in range(n)]

for i in range(n):
    for j in range(i):
        if arr[i] > arr[j]:
            length[i] = max(length[i], length[j] + 1)

print(max(length))

기존에는 저장 된 배열의 가장 큰 값보다 작은 값이 들어오면, 모든 인덱스를 탐색해서 배열의 값을 초기화 해주었다.

이렇게 되면 O(N^2)의 시간복잡도를 가지게 된다.

하지만, 모든 인덱스를 굳이 탐색하지 않아도, 저장 된 배열의 가장 큰 값보다 큰 값만이 배열에 추가된다.

즉, DP 테이블의 값들은 모두 정렬이 되어있는 것이다.

---

📌 Binary Search

이미 정렬된 리스트에서 값을 찾을 경우, 이진 탐색은 매우 효과적이다. O(logN)

그래서 위 코드에서, 마지막 값 보다 작은 값이 들어올 경우의 수만 수정해준다.

import sys

input = sys.stdin.readline

n = int(input())

arr = list(map(int, input().split()))
dp = [0]

for i in range(n):
    if arr[i] > dp[-1]:
        dp.append(arr[i])
    elif arr[i] < dp[-1]:
        start, end = 0, len(dp) - 1
        target = arr[i]
        while start < end:
            mid = (start + end) // 2

            if dp[mid] < target:
                start = mid + 1
            else:
                end = mid

        dp[end] = target

print(len(dp) - 1)

마지막 값보다 작은 값이 들어올 경우, 가장 긴 증가하는 부분수열이 바뀔 수 있기 때문에 무조건 수정을 해야한다.