트리에는 정말 많은 종류가 있다. 그중 대표적으로 살펴볼 것들
- tree
- binary tree
- binary search tree
비교. 이진 검색 트리는 BST라고 줄여 말한다.
tree
트리는 연결 리스트처럼 노드로 이루어진 데이터 구조이다.
차이점은 노드들 사이에 부모-자식 관계가 있다. 그래서 가지를 가지게 된다.
가문의 가계도처럼 보인다. 실제 나무처럼 줄기에서 뻗어나온 수많은 가지들이 나뉜 모양.
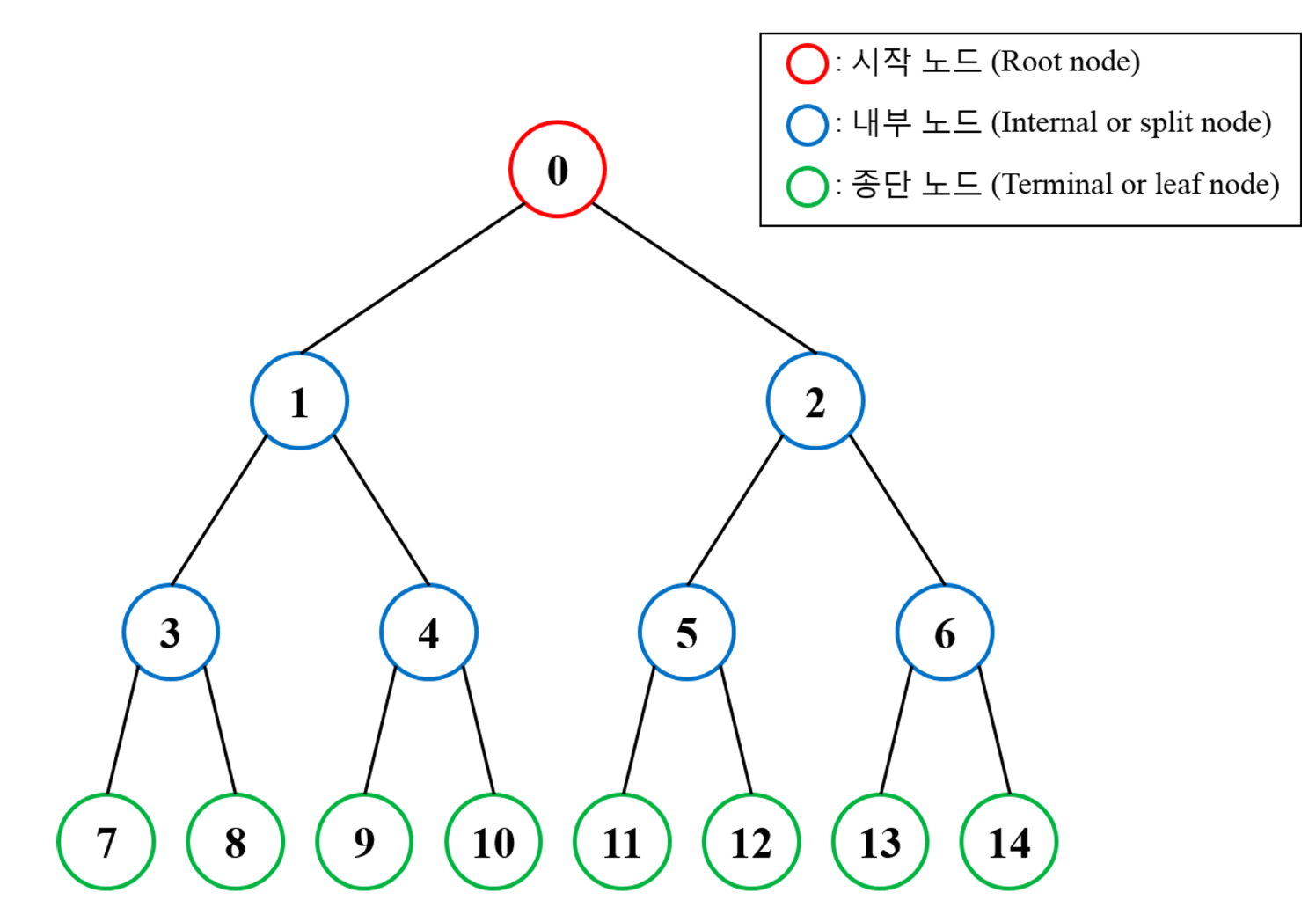
가장 꼭대기에 있는 노드는 루트라고 부른다.
각 노드들은 한개, 여러개 또는 0개의 노드를 가리킬 수 있다.
연결 리스트와 트리 비교
- 리스트는 linear
- 트리는 nonlinear
리스트는 선형 구조. 모든 것이 한 줄로 늘어서 있다.
트리는 비선형이다. 한 갈래가 아닌 여러 줄로 늘어서 있음.
리스트가 트리의 한 종류라고 볼수도 있다.
tree의 규칙
노드는 부모-자식 관계에 따라서 자식인 노드만을 가리킬 수 있다.
자식이 부모를 가리키거나 형제 노드를 가리키면 안된다.
또한 루트는 하나여야만 한다. 루트가 두개이면 트리가 아니다
- root : 트리의 꼭대기에 있는 노드
- child : 루트에서 멀어지는 방향으로 연결된 노드
- parent : 자식의 반대 개념
- siblings : 같은 부모를 가지는 노드
- leaf : 자식이 없는 노드
- edge : 간선. 한 노드에서 다른 노드로 향하는 화살표. 연결.
tree가 사용되는 곳
- HTML, DOM
- 네트워크 라우팅
- Abstract syntax tree 추상 구문 트리
- 인공지능 머신러닝
- 운영체제의 folder 시스템
- JSON
Binary search tree
binary tree 이진 트리
이진트리는 각 노드가 최대 두 개의 자식을 가져야 한다는 특별한 조건이 있다.
각 노드는 자식이 0개, 1개, 2개인 것이다.
보통 루트 노드는 2개의 자식 노드를 가진다.
Binary search tree 이진 탐색 트리는 이진 트리의 한 종류이다.
이진 탐색 트리는 특별한 방식으로 정렬되어 있다. 데이터가 순서에 따라 저장되어 있음.
BST는 데이터를 비교해서 정렬 가능하게 저장한다.
일반적으로 숫자를 다룸. 숫자가 아니어도 되지만 그것들을 비교하고 순서를 매기는 방법이 있어야한다.
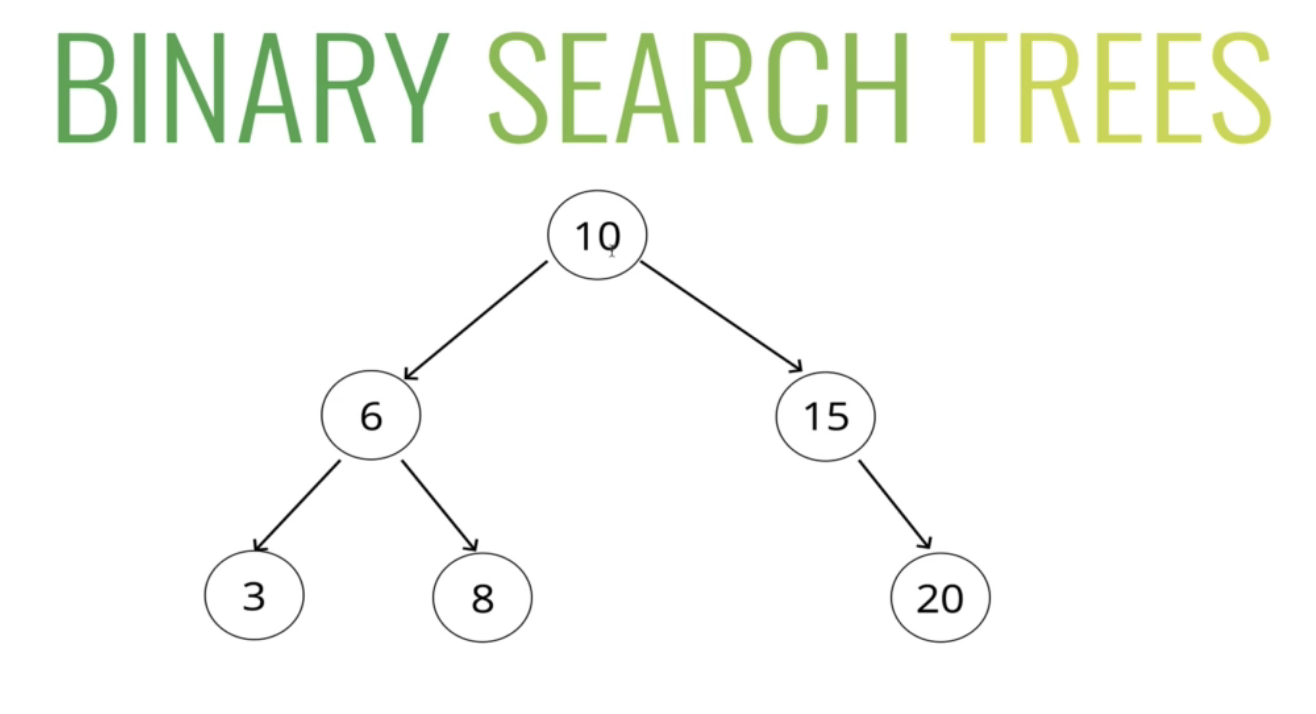
특징
- 모든 부모 노드는 최대 2개의 자식 노드를 가진다
- 부모 노드의 왼쪽에 있는 노드는 항상 부모 노드보다 작은 값이다
- 부모 노드의 오른쪽에 있는 노드는 항상 부모 노드보다 큰 값이다.
루트 노드인 10. 10보다 작은 요소는 왼쪽에 위치한다. 10보다 큰 숫자는 오른쪽에 위치한다.
각 자식 노드들에서도 반복된다. 왼쪽 자식 노드 6 밑으로는 6보다 작은 3이 왼쪽, 6보다 큰 8이 오른쪽.
이진 검색 트리의 장점
탐색을 할때 매우 빠르다. 찾는 값보다 큰지 작은지를 판단하여 매번 비교를 할때 절반 씩 줄어들게 된다.
모든 노드를 다 돌면서 순회하는 것보다, 한번 비교할때마다 절반씩 지워지기 때문에 매우 빠르다.
Binary search tree 구현
class Node {
constructor(value){
this.value = value; // 노드를 새로 만들면 val 값에 저장
this.left = null; // left와 right 기본값은 null.
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
}
var tree = new BinarySearchTree();
tree.root = new Node(10); // 먼저 트리를 만들고 root를 새로 노드를 만들어서 할당.
tree.root.right = new Node(15);
tree.root.left = new Node(7);
tree.root.left.right = new Node(9);연결 리스트를 구현한 클래스에서 next와 prev이 있었다면, 이진 검색 트리에서는 left와 right가 있다.
insert()
트리에다 새로운 노드를 추가하는 메서드
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){ // root가 없으면 root로 할당.
this.root = newNode;
return this;
}
var current = this.root; // current를 root로 잡아주고
while(true){ // 넣을 위치를 찾기 위해 while 반복문. return될때까지 반복.
if(value === current.value) return undefined; //새로 넣을 값이 이미 있다면 undefined.
if(value < current.value){ // 현재 노드의 값보다 새로 넣을 값이 더 작다면
if(current.left === null){ // 현재 노드의 left가 비었다면
current.left = newNode; // left에 새로 넣을 값 넣어줌
return this; // return.
}
current = current.left; // 현재 노드의 left가 있다면 current가 left로 바뀜.
} else { // 현재 노드의 값보다 새로 넣을 값이 더 크다면
if(current.right === null){ // right가 없다면
current.right = newNode; // right에 넣음
return this; // return.
}
current = current.right; // right가 있으면 current가 right로 바뀜.
}
}
}
}어딘가에 들어갈때까지 while이 돈다.
find()
입력받은 값이 트리에 있는지 탐색.
insert와 비슷하다. 현재 노드와 비교하여 작으면 left, 크면 right로 가는걸 반복한 후
바닥에 도달해서 다음 노드가 없다면 해당 값이 없다는 것을 의미한다.
find(value){
if(this.root === null) return false; // 빈 트리라면 false를 리턴.
var current = this.root, // root를 current 현재 노드로 시작.
found = false; // 찾았는지를 나타내는 변수
while(current && !found){ // 현재 노드가 있고, found가 false이라면 계속 반복
if(value < current.value){ // 찾는 값이 현재 노드의 값보다 작다면
current = current.left; // 현재 노드는 left로 바뀜
} else if(value > current.value){ // 찾는 값이 현재 노드의 값보다 크다면
current = current.right; // 현재 노드는 right로 바뀜.
} else { // 찾는 값이 현재 노드 값보다 작지도 크지도 않으면 같다는 뜻이므로
found = true; // found가 true로 바뀌며 반복 종료.
} // 만약 찾지 못하면 바닥에서 current.left나 right가 없을것이므로 current는 null이 되고 역시 반복 종료.
}
if(!found) return undefined; // 찾지 못했다면 undefined를 리턴.
return current; // 찾았다면 current를 리턴.
}Binary search tree의 Big-O
- insertion - O(log n)
- searching - O(log n)
최선의 경우 log n 의 시간복잡도를 가진다.
최악의 경우 : 트리가 한 방향으로만 이어진 연결 리스트와 같은 모양이라면 매번 비교해도 한번 비교할때 한개씩 밖에 제거하지 못한다. 즉 이 경우 O(n)이 된다.
- 최악의 경우 : O(n)
이런 데이터라면 이진 트리가 아니라 다른 데이터구조를 써야 한다.
