정렬되지 않은 이진 트리를 탐색하는 널리 사용되는 방법 4가지가 있다.
각각 순서대로 이름이 있다.
재귀를 많이 사용한다
- Breadth-first Search 너비 우선 BFS
- Depth-first Search 깊이 우선 DFS
각 트리가 생긴 모양이 다른 만큼 다른 전략의 트리들이 데이터에 따라 다른 효과를 가진다
Breadth-first Search (너비 우선, BFS)
BFS는 가로로 가로질러서 작업을 한다. 좌우인지 우좌인지는 중요하지 않음. 수평으로 작업하고 있다는 사실이 중요하다.
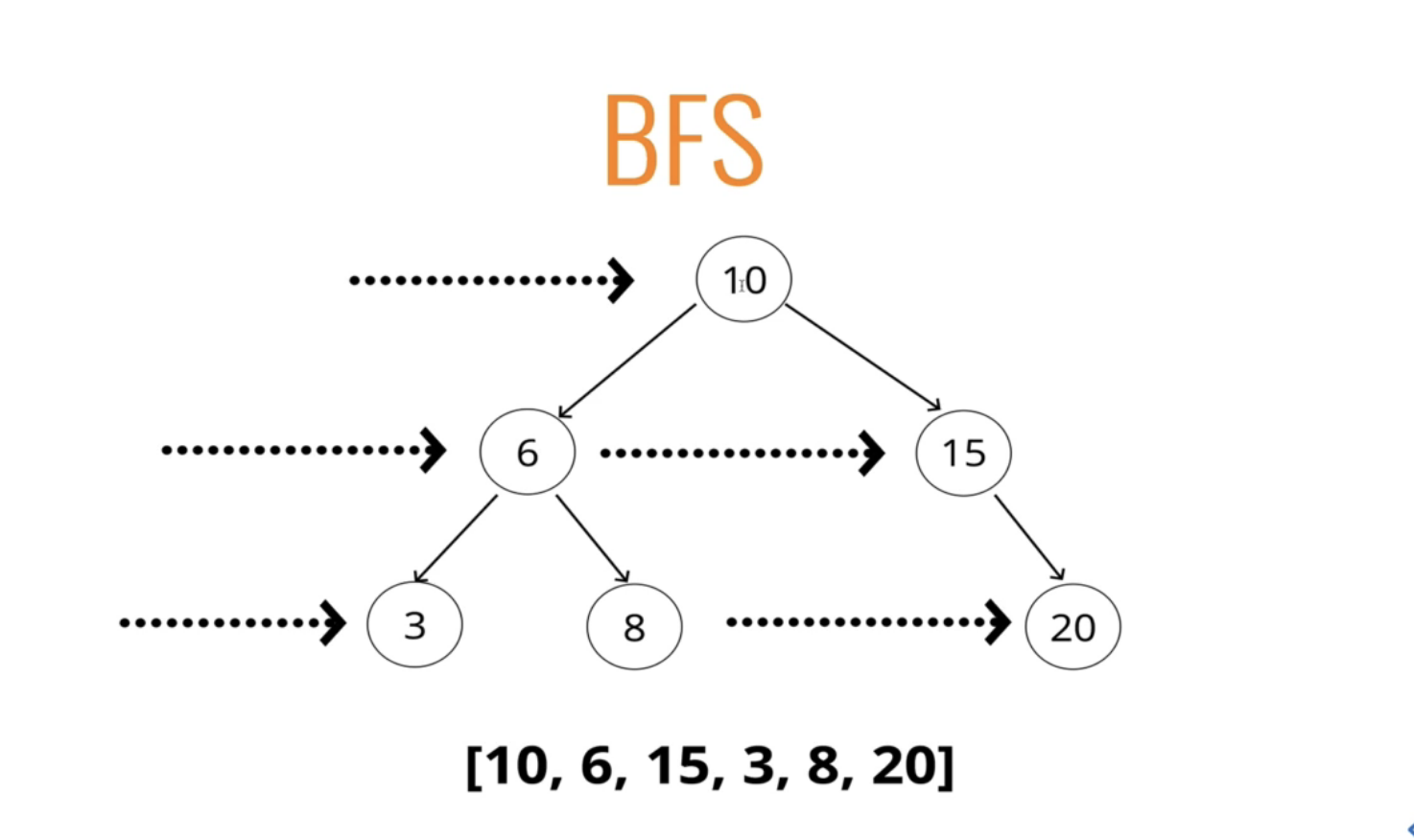
DFS는 3가지 순서가 있다
깊이 우선은 기본적으로 일차적인 진행 방향이 트리의 수직 방향 끝이고, 거기까지 간 다음 다시 올라온다.
큐를 사용해서 구현한다. 큐는 선입선출 구조.
BFS 구현
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
var newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
var current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
var current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
var current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
} // 위까지는 이진 탐색 트리.
BFS(){
var node = this.root, // 노드는 root로 시작
data = [], // 리턴할 data 배열
queue = []; // 큐 배열
queue.push(node); // root 노드를 큐에 넣는다
while(queue.length){ // 큐가 빈 배열이 아니면 계속 반복
node = queue.shift(); // 큐의 맨 앞에 있는 엘리먼트를 노드로 한다
data.push(node.value); // data배열에 노드의 값을 push한다
if(node.left) queue.push(node.left); // 만약 노드의 left가 있다면 큐에 추가
if(node.right) queue.push(node.right); // 만약 노드의 right가 있다면 큐에 추가
} // 만약 이진트리가 아닌 삼진트리라면 첫번째, 두번째, 세번째 push를 해야함
return data; // data 리턴
}
}Depth-first Search (깊이 우선, DFS)
DFS는 일단 맨 아래 노드까지 깊이로 내려간다. 그 다음 순서에 따라 여러개로 나뉜다.
어떤 노드든지 결국에는 언젠가 노드 자체에 도달해야만 한다
2-3-1 순서로 볼것.
1. DFS - InOrder 정위 순회
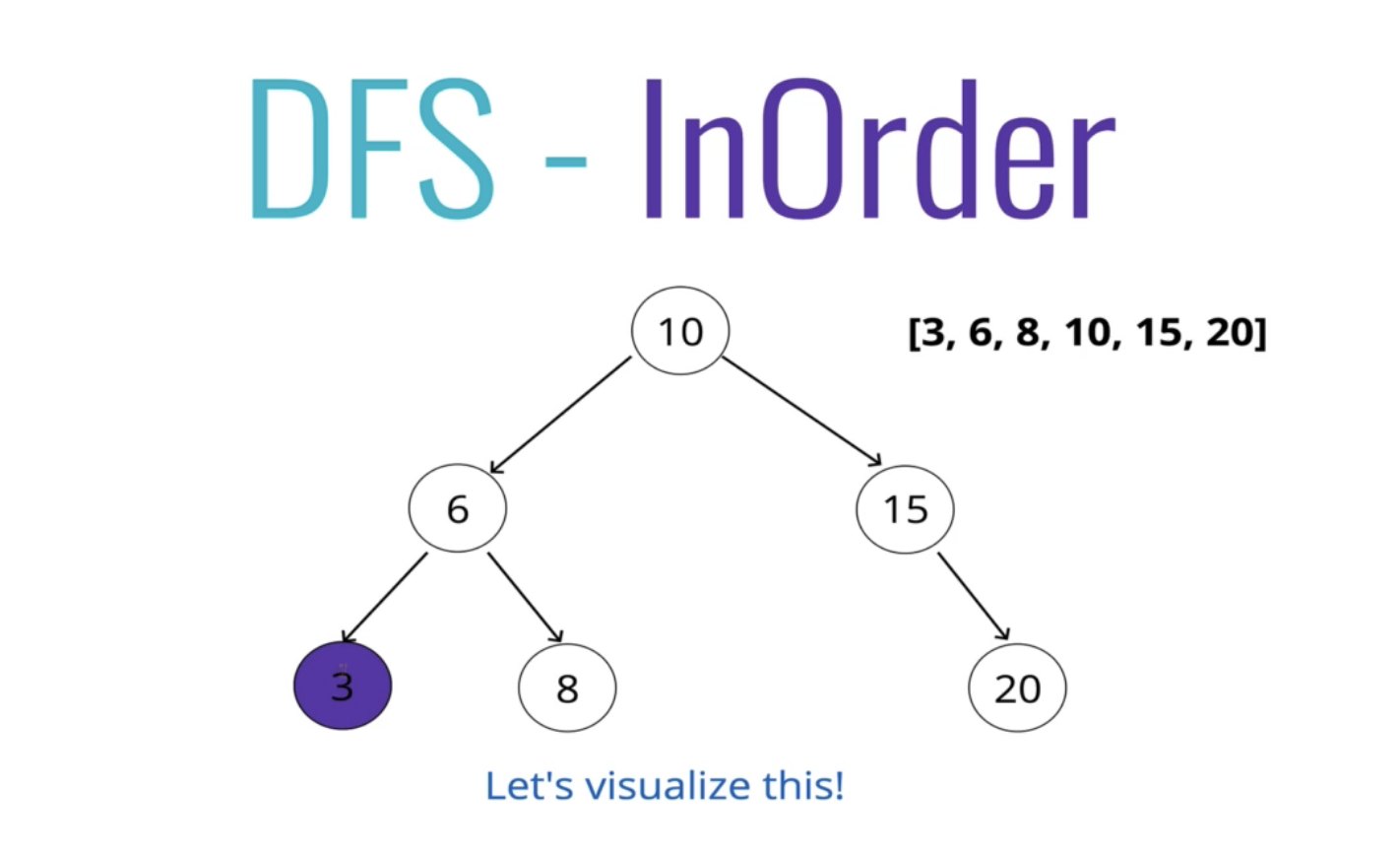
정위 탐색에서는 먼저 왼쪽 전체를 순회하고 노드를 거쳐 오른쪽 전체를 순회한다.
역시 전위 탐색이나 후위 탐색과 헬퍼함수의 순서만 조금 다르다.
DFSInOrder(){
var data = [];
function traverse(node){
if(node.left) traverse(node.left); // 왼쪽을 먼저 재귀적으로 헬퍼함수 호출하고
data.push(node.value); //노드의 값을 데이터에 넣는다.
if(node.right) traverse(node.right); // 그 다음에 오른쪽 헬퍼함수 호출.
}
traverse(this.root);
return data;2. DFS - PreOrder 전위 순회
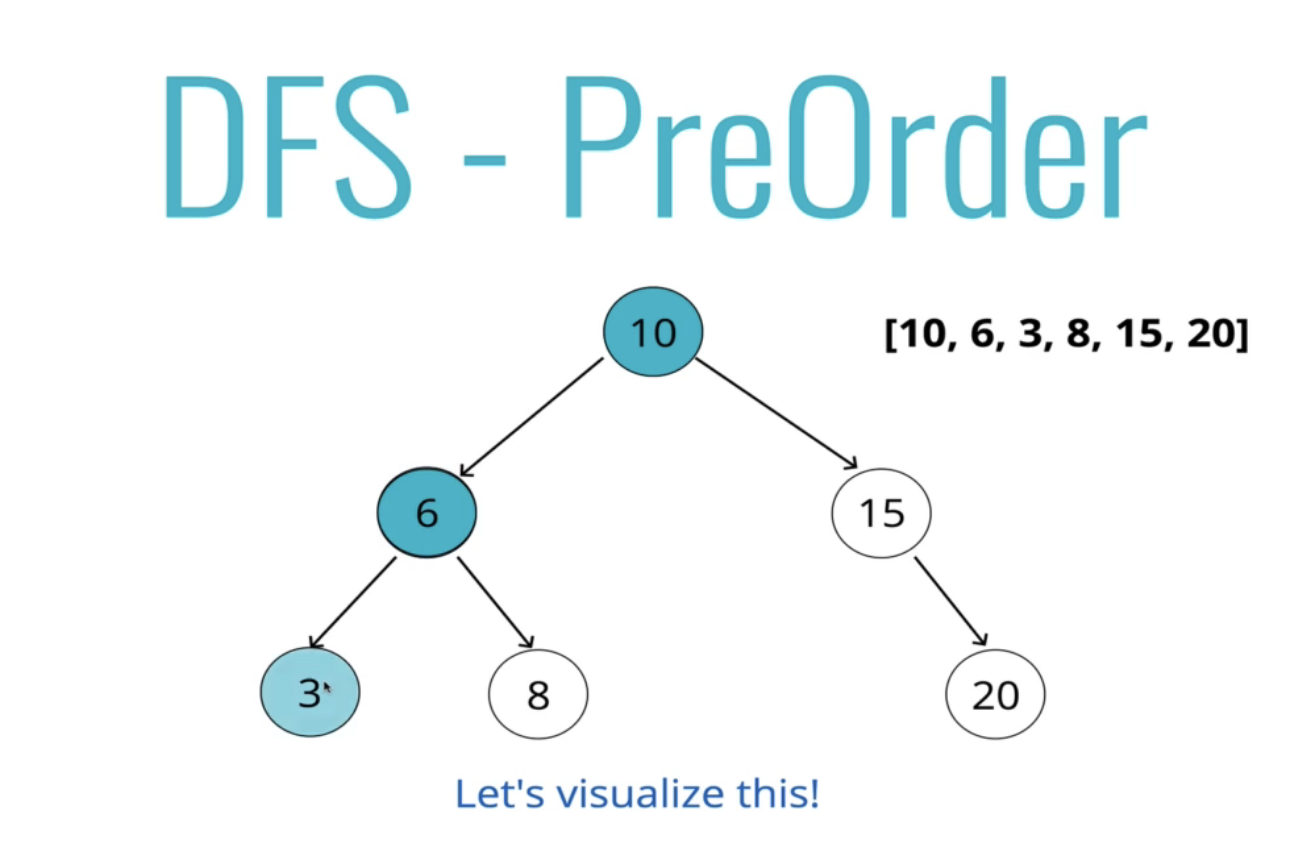
전위 탐색은 맨 왼쪽 아래 노드에 접근 다음 왼쪽 전체를 보는 것. 왼쪽을 순회한 다음 오른쪽을 순회한다.
모든 노드에 대해서 이렇게 진행한다.
헬퍼 함수를 만든 뒤 그것을 재귀를 사용해서 호출한다
헬퍼 함수는 노드의 값을 data 배열에 넣고, 왼쪽을 먼저 재귀적으로 헬퍼함수 호출한다. 그러면 맨 왼쪽 아래까지 내려감.
재귀: 어떤 종료점에 도달할 때까지 더 작은 부분이나 변경되는 부분에서 반복적으로 수행.
재귀함수의 두가지 조건. 1. 자기 자신을 재귀적으로 호출. 2. 중단점이 있을 것.
재귀함수는 콜스택에 쌓인다. 콜스택은 위에부터 사라진다. 후입선출.
DFSPreOrder(){
var data = [];
function traverse(node){ // 헬퍼 함수
data.push(node.value); // data배열에 값을 넣는다
if(node.left) traverse(node.left); // 현재 노드 밑에 left가 있으면 left에 헬퍼함수 재귀적으로 요청한다.
if(node.right) traverse(node.right); // 왼쪽이 끝나면 오른쪽.
}
traverse(this.root); // 루트에서 시작한다.
return data;
}3. DFS - PostOrder 후위 순회
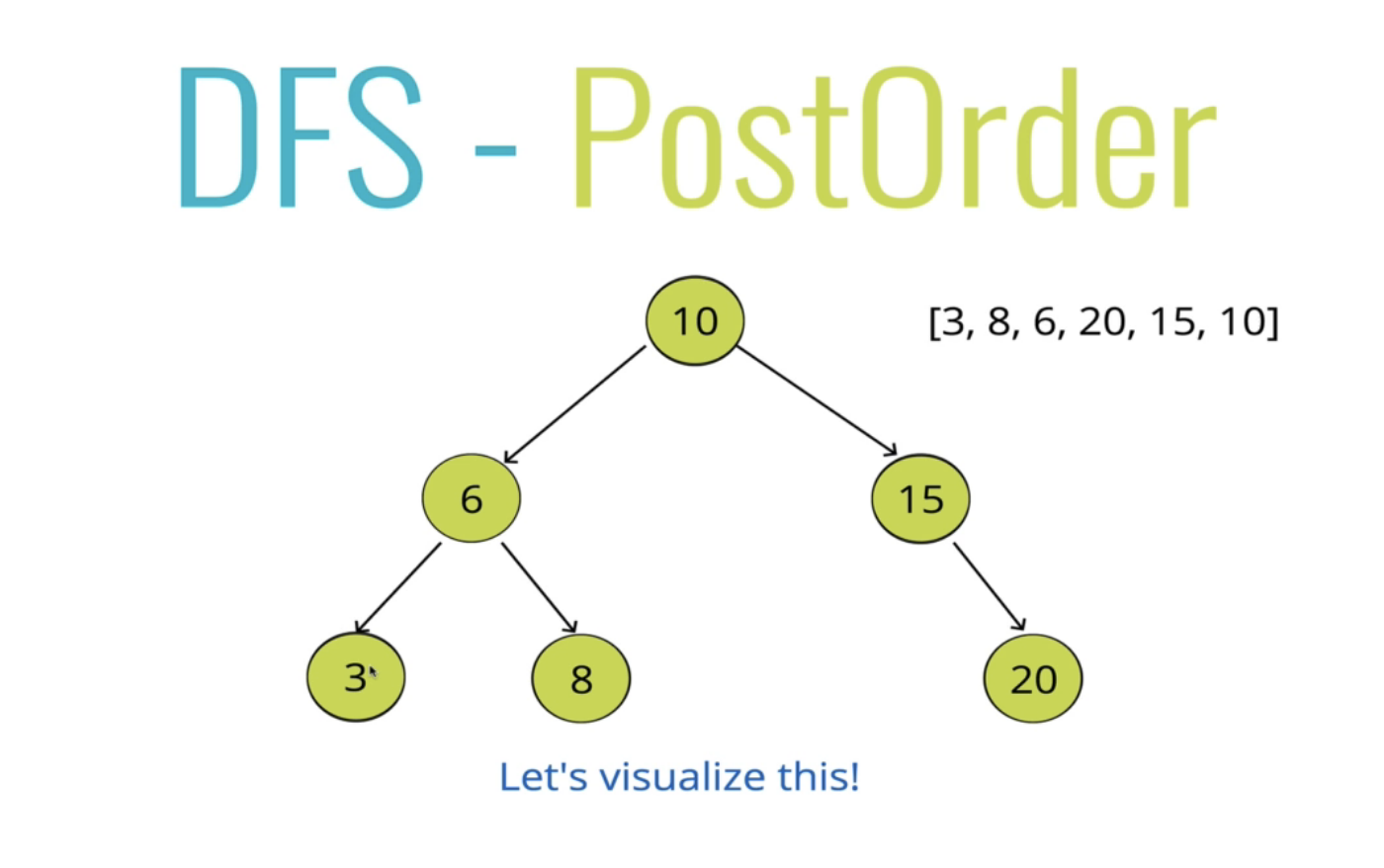
후위 탐색은 노드를 나중에 방문하고, 오른쪽과 왼쪽을 순서대로 돈다
즉 아래로 모든 것을 먼저 탐색한다. 노드에 달린 전체 가지인 왼쪽과 오른쪽을 먼저 순회하고 나서 노드를 방문한다
전위 탐색과 비슷하다.
DFSPostOrder(){
var data = [];
function traverse(node){
if(node.left) traverse(node.left); // 노드의 왼쪽부터 재귀적으로 헬퍼함수 호출
if(node.right) traverse(node.right); //
data.push(node.value); // data배열에 넣는 것을 마지막으로 수행함. 즉 밑에 아무것도 없으면 그제야 넣는다.
}
traverse(this.root);
return data;
}전위 탐색과 헬퍼 함수 내부의 코드 순서만 바꿨는데 완벽히 돌아간다. 재귀의 효과
BFS와 DFS의 장단점
각각 어떤 상황에서 베스트인가?
시간복잡도느 같다. 모든 노드를 한번씩 방문하니까 관계가 없다.
공간복잡도가 차이난다.
- 매우 넓고 깊이는 얇은 트리에 대해서 너비 우선탐색 BFS를 쓰면 큐에 아주 많이 넣어야한다.
DFS를 쓰면 트리를 가로질러 가면서 넓은 노드들을 전부 저장할 필요가 없다. 깊이까지만 내려가면 된다.
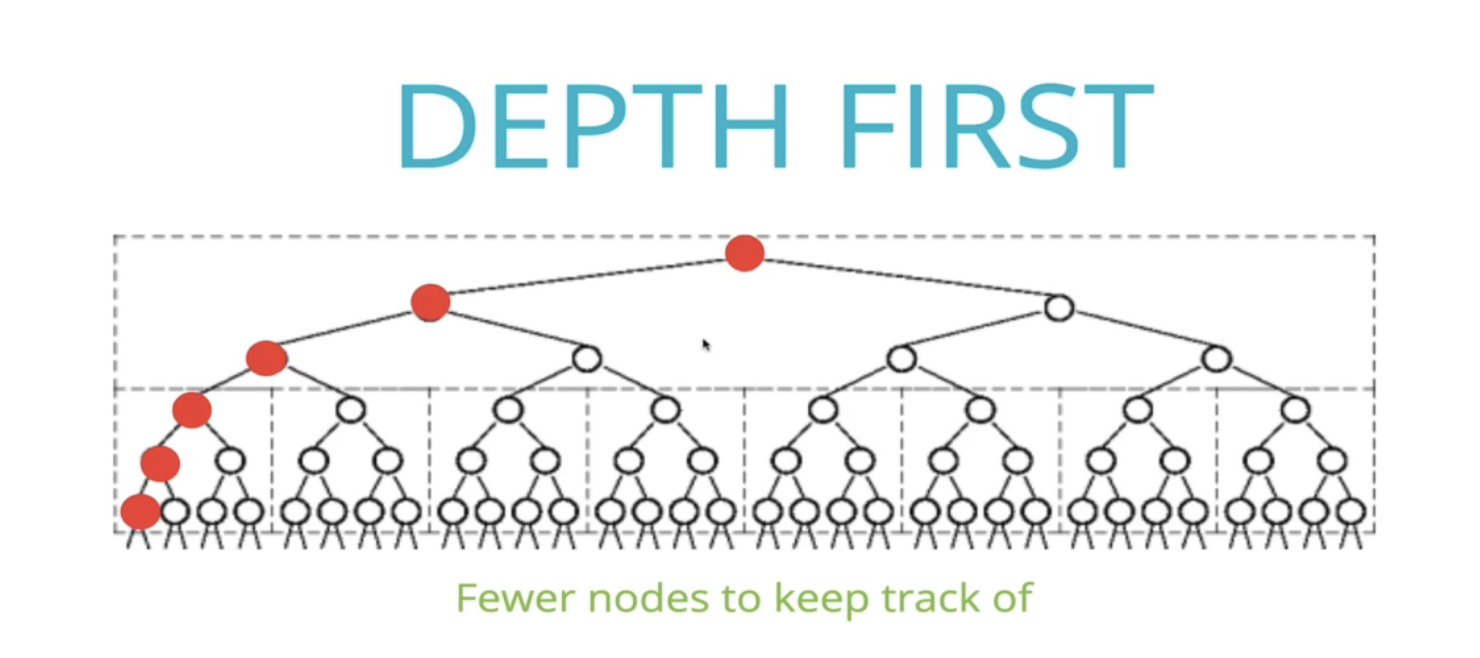
- 좁고 깊은 트리에서는 DFS를 쓰면 그 깊이까지 전부 메모리에 저장해야 한다. 이럴때는 BFS가 낫다

그렇다면 DFS에서 전위, 후취, 정위는 어떻게 사용하나?
- 정위 탐색: 모든 노드를 오름차순으로 구하게됨
- 후위 탐색: 트리를 export할때 사용할수 있다. 즉 트리를 복사하거나 평탄화해서 저장하는 경우, 그것을 다시 구조로 만들어 낼때 도움이 된다.
정리
- 시간복잡도는 같음. 공간복잡도에서 차이난다
- 넓고 얕은 트리는 DFS가 낫다
- 좁고 깊은 트리는 BFS가 낫다
