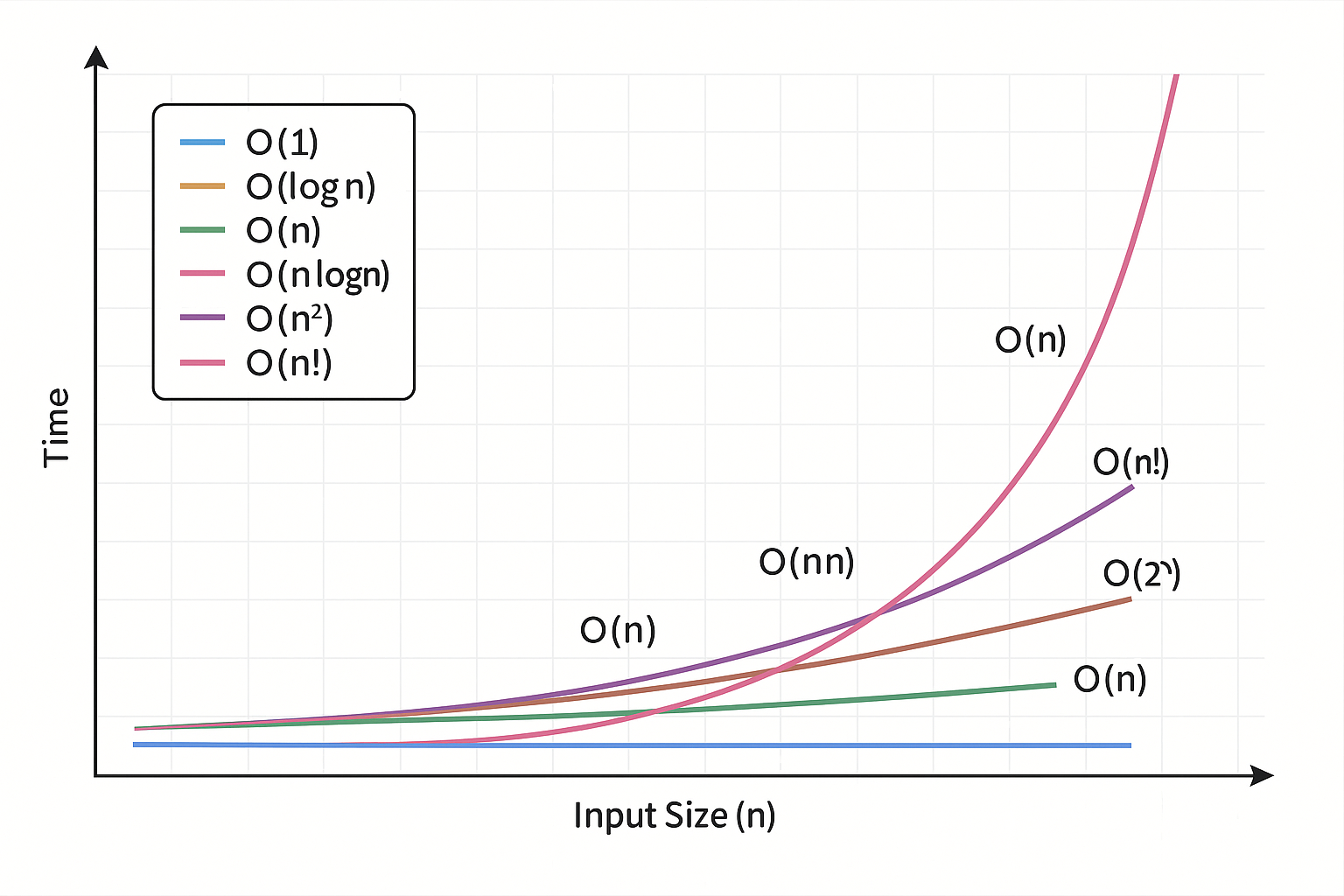
시간복잡도
시간복잡도는 입력 크기 n이 커질수록 알고리즘이 수행해야 하는 연산 횟수의 증가 정도를 표현한 것 입니다.
주로 Big-O 표기법을 이용해서 O(n), O(log n), O(n²) 등으로 표현합니다.
시간복잡도 표
다음은 chatGPT를 이용해 시간복잡로를 표로 정리한 모습입니다.
| 표기 | 이름 | 예시 |
|---|---|---|
| O(1) | 상수 시간 | 배열 인덱스 접근 - arr[3] |
| O(n) | 선형 시간 | 단순 for문 |
| O(n²) | 2차 시간 | 이중 for문 |
| O(n!) | 팩토리얼 시간 | 순열/조합 완전탐색 |
| O(2ⁿ) | 지수 시간 | 피보나치 재귀 |
| O(log n) | 로그 시간 | 이진 탐색 |
| O(n log n) | 로그 선형 | 병합 정렬, 퀵 정렬 |
| 입력 크기(n) | 1 | 10 | 100 | 1,000 | 10,000 |
|---|---|---|---|---|---|
| O(1) | ✅ | ✅ | ✅ | ✅ | ✅ |
| O(n) | ✅ | ✅ | ✅ | ✅ | ✅ |
| O(n²) | ✅ | ✅ | ⚠️ | ❌ | ❌ |
| O(n!) | ✅ | ❌ | ❌ | ❌ | ❌ |
| O(2ⁿ) | ✅ | ⚠️ | ❌ | ❌ | ❌ |
| O(log n) | ✅ | ✅ | ✅ | ✅ | ✅ |
| O(n log n) | ✅ | ✅ | ✅ | ✅ | ⚠️ |
✅ : 통과
⚠️ : 위험
❌ : 시간초과
위 표가 정확히 무슨 의미인지 하나하나 접근해 보겠습니다.
시간복잡도 알아보기
O(1) 상수 시간
핵심키워드 : 단순연산, 조건문, 해시접근(map[key])
상수 시간은 특정 인덱스를 콕 찝어내기 때문에 입력크기 n과는 상관없이 일정한 시간이 걸립니다.
특징
- 가장 빠른 복잡도
- 테이블,배열에 직접 접근, 변수 연산 등
예시 문제
Q. 배열의 첫번째 요소를 반환하시오.
function getFirstElement(arr: number[]): number {
return arr[0]
}
getFirstElement([3,2,6,3,4,2,3]); // 입력크기와 상관없이 0번째 반환.O(n) 선형 시간
핵심키워드 : 단일 for문, filter, map, reduce, 배열/문자열 탐색, 최대값, 최소값
선형시간은 입력 크기만큼 시간이 걸리는 알고리즘입니다. 주로 단일 for문에 사용됩니다.
특징
- 가장 많이 나오는 복잡도
- 단일 반복문의 형태
예시 문제
Q. 배열에서 가장 큰 값을 구하시오.
function getBiggestNumber(arr: number[]): number {
let result = 0;
for(let i = 0; i < arr.length; i++) {
if(arr[i] > result) {
result = arr[i]
}
}
return result;
}
getFirstElement([3,2,6,3,4,2,3]); // 입력크기 만큼 순회하여 가장 큰값을 반환.O(n²) 2차 시간
핵심키워드 : 이중 for문, 버블정렬
2차 시간은 입력 요소마다 또다른 모든 요소를 순회하는 n개의 값을 가진 배열을 O(n)으로 순회할때 그안에서 새로 또 n개의 값을 가진 배열을 순회한다면 O(n * n) = O(n²) 이 되는 알고리즘입니다.
특징
- 이중 반복문에서 자주 발생
- 데이터가 조금만 커져도 제곱으로 시간이 늘어나기에 느려짐
- 완전탐색류, 브루트포스 등에서 사용
예시 문제
Q. 빨강, 흰색, 파랑 색의 객체가 n개인 배열이 주어졌을 때, 같은 색의 객체가 빨강, 흰색, 파랑 순서로 인접하도록 제자리에서 정렬하시오.
정수 0, 1, 2를 사용하여 각각 빨간색, 흰색, 파란색을 냄.
function sortColors(nums: number[]): void {
for(let i = 0; i < nums.length; i++) {
for(let j = 0; j < nums.length - i - 1; j++) {
if(nums[j] > nums[j+1]) {
let temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
}
}
}
console.log(nums);
};
sortColors([2,0,2,1,1,0]);nums의 length인 6번의 순회 속에서 또다시 nums의 length를 기반으로 i만큼 차감하여 반복하게됩니다.
이는 결국 n² 에 근접하게 됩니다.
O(n!) 팩토리얼 시간
핵심키워드 : 팩토리얼, 조합 백트래킹(모든 경우 탐색), 외판원 문제
n! 에서 알수 있다시피 입력한 n개를 모든 순열/조합으로 나열할 때 사용하는 알고리즘입니다.
특징
- 팩토리얼 특성상 느림(시간복잡도 중 가장느림)
- 10 이상만 넘어가도 시간초과가 생기기 때문에 10이하에서 사용 권장합니다.
예시 문제
Q. 숫자 배열의 모든 순열을 구하시오.
// chatGPT 참고... 추후에 직접 구현해볼 예정.
function permute(arr: number[]): number[][] {
const result: number[][] = [];
const getPermutation = (path: number[], rest: number[]) => {
if(rest.length === 0) {
result.push([...path]);
return;
}
for(let i = 0; i < rest.length; i++) {
const next = rest[i];
const nextRest = [...rest.slice(0, i), ...rest.slice(i + 1)];
getPermutation([...path, next], nextRest);
}
}
return result;
}
permute([1,2,3])O(2ⁿ) 지수 시간
핵심키워드 : 백트래킹, 조합/부분집합 완전탐색, DFS, 피보나치수열
입력 요소마다 또 다른 모든 요소를 순회하는 알고리즘입니다.
특징
- 매우 느린편. 10개의 입력 요소만 존재해도 2의 10승의 시간이 걸립니다..
- 재귀호출 방식 + 중복계산이 존재합니다.
- 반드시 메모이제이션이 필요합니다.
예시 문제
Q. 정수 배열 nums와 정수 maxSum이 주어집니다.
nums의 모든 부분집합 중에서, 원소의 합이 maxSum 이하인 부분집합들만 구하세요.
function subsets(nums: number[], maxNum: number): number[][] {
const result: number[][] = [];
const dfs = (path: number[], index: number) => {
const sum = path.reduce((acc, curr) => acc + curr, 0);
if (sum <= maxNum) {
result.push([...path]);
}
for (let i = index; i < nums.length; i++) {
path.push(nums[i]);
dfs(path, i + 1);
path.pop();
}
};
dfs([], 0);
return result;
}
sunsets([1,2,3], 4)2ⁿ이라는 시간복잡도에 의해 해당 배열은 2^3 = 8번 순회하게 될껍니다.
dfs를 통한 배열의 순회는 다음과 같습니다.
[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]
그리고 해당 순회를 통해 합이 4보다 큰 값들을 출력하게됩니다.
O(log n) 로그 시간
핵심키워드 : 이진 탐색, 트리 탐색, Map/Set 내부 탐색
데이터를 매번 절반씩 줄여가며 탐색하는 방식
특징
- 데이터가 클수록 효율
- 정렬된 데이터일때 사용 가능
- log₂n 기준 (이진트리 깊이와 동일)
예시 문제
Q. 배열 arr에서 특정 값 k를 이진 탐색으로 찾기.
function binarySearch(arr: number[], k: number): boolean {
const sortArr = arr.sort((a, b) => a - b);
let low = 0;
let high = sortArr.length - 1;
while (low <= high) {
const mid = Math.floor((low + high) / 2);
if (arr[mid] === k) return true;
if (arr[mid] < k) low = mid + 1;
else high = mid - 1;
}
return false;
}
console.log(binarySearch([2, 8, 7, 5, 3, 4, 2, 10, 38], 7));log n 에 의해 log 9 = 3회의 순회를 하게됩니다. 해당 예시는 특정값 k를 이진탐색으로 찾기위해 최초에 배열을 정렬 해주는 과정을 거쳤습니다.
이후 0 부터 sortArr.length - 1을 각각 low, high로 적용하여 배열의 첫번째 인덱스와 마지막 인덱스를 기반으로 중심값을 k값을 찾기 위해 비교분석에 들어갑니다.
정렬된 배열: [2,2,3,4,5,7,8,10,38]
1번째 탐색 : (0+8)/2 = 배열의 4번째 = 5는 k인 7보다 작기때문에 low = mid+1 = 5가 됩니다.
2번째 탐색 : (5+8)/2 = 배열의 6번째인 8은 k보다 크기때문에 high = mid-1 = 5가 됩니다.
3번재 탐색 : hight가 low보다 크거나 같을경우 반복하기에 사실상 마지막 탐색입니다. arr[5]의 값인 7은 k와 같기때문에 true가 반환되고 해당 탐색은 종료됩니다.
log n = log 9 = 3 에 맞게 3번의 탐색을 통해 찾은모습을 볼 수 있습니다.
O(n log n) 로그 선형
핵심키워드 : Array.sort() -> timsort기반, Quick, Merge, 균형트리
입력 크기만큼 반복하면서 각 단계마다 log n만큼의 연산이 필요한 경우
특징
- 효율적 정렬 알고리즘의 핵심
- 정렬 알고리즘에서 등장: MergeSort, QuickSort
- 이진 트리 기반 작업을 n번 반복하는 경우
예시 문제
Q. 숫자 배열을 오름차순으로 정렬하라
function sortArray(arr: number[]) : number[] {
return arr.sort((a,b) => a - b);
}
sortArray([2,6,30,4,11,0,1,8,8,2,13,17]);12 log 12 = 12 (log 12) -> log 12 = 약 3.58 -> 12 3.58 = 42.96.
위 정렬은 대략 42.96번 정렬한다고 생각할 수 있습니다.

실제로 지피티를 통해 해당 횟수와 근사하게 반복한다는 결과를 도출할 수 있었습니다.
여담
시간 복잡도를 이해하고 관련 문제들을 풀어보면서도 아직 완벽하게 이해하진 못한거 같다 라는 생각이 들었습니다.
비교적 쉬운 시간 복잡도도 있는 반면, 지수나 팩토리얼 같은 복잡하고 이해하기 쉽지않은 복잡도도 많았습니다.
향후에 공간 복잡도와 알고리즘에 대한 글을 작성하면서 더 자세히 알아보고, 이해하는 시간을 가져야 할 꺼 같습니다.