[LeetCode] Algorithm/Search Insert Position/LeetCode 35

이 문제는 배열 내에 target이 위치해야 할 인덱스를 도출하는 로직을 구현해야 한다.

제한사항(시간복잡도를 O(log n))이 존재하기 때문에 이진 탐색을 사용해야하며,
for문은 O(n)의 시간 복잡도를 가지기 때문에 이를 베이스로 하는 includes,map, find와 같은 내장함수는 사용할 수 없다.

이진탐색 알고리즘의 개념

이진탐색 알고리즘은 정렬된 리스트에서 검색 범위를 줄여가며 정답을 찾는 개념으로

리스트가 오름차순 혹은 내림차순으로 정렬되어야 사용할 수 있고,
검색횟수가 늘어날 때마다 검색 범위는 n/2로 줄어들기 때문에 속도가 빠르다.

이진탐색 알고리즘의 동작원리

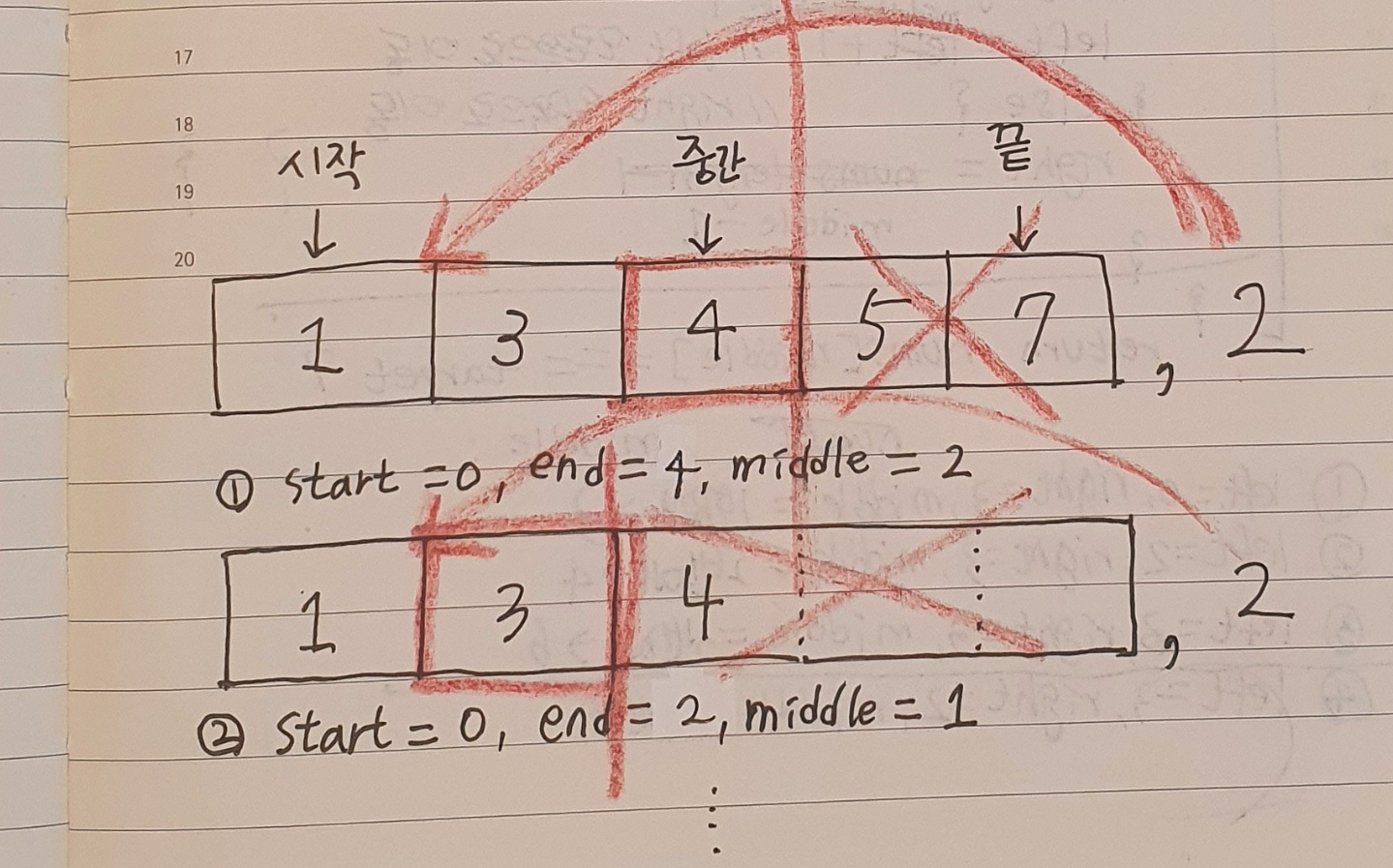
1. 배열에서 시작, 중간, 끝 인덱스를 설정한다.

2. 타켓 값이 중간값(배열[중간 인덱스])과 같으면 해당 인덱스를 리턴한다.

3. 시작 인덱스가 끝 인덱스보다 커질 때까지 조건을 테스팅한다.

3-1) 타겟 값이 중간값(배열[중간 인덱스])보다 크면, 시작 인덱스를 중간 인덱스+1 로 다시 세팅한다.
	=> 중간 인덱스를 기준으로 타켓은 오른쪽에 위치하기 때문에 중간 인덱스 왼쪽 데이터들은 무용지물이다.

3-2) 타겟 값이 중간값(배열[중간 인덱스])보다 작으면, 끝 인덱스를 중간 인덱스-1 로 다시 세팅한다.
	=> 중간 인덱스를 기준으로 타켓은 왼쪽에 위치하기 때문에 중간 인덱스 오른쪽 데이터들은 무용지물이다.

3-3) 시작 혹은 끝 인덱스가 변화됨에 따라 중간 인덱스를 다시 설정한다.

4. 테스팅 조건에 부합하지 않으면, 코드의 종료와 함께 값을 리턴한다.

이진탐색 알고리즘의 코드

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
 
var binarySearch = function(nums, target) {
    let left = 0;
    let right = nums.length-1;
    let middle = Math.ceil((left+right)/2)
    while(nums[middle] !== target && left <= right){
        if(target > nums[middle]){
            // middle기준 오른쪽에 있기 때문에 left의 위치가 middle인덱스+1
            left = middle +1
        }else {
            //  target이 middle인덱스값보다 작으면 middle기준 왼쪽에 위치하니까 right의 인덱스는 middle인덱스 -1
            right = middle -1
        }
        middle = Math.floor((left+right)/2)
    }
    return target === nums[middle] ? middle : left
}