[Leetcode] Easy-Valid Parentheses

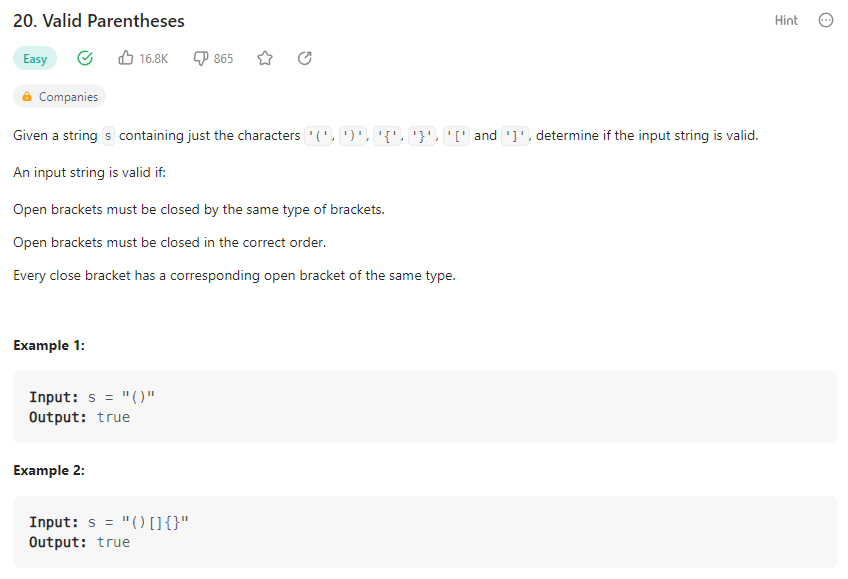
주어진 괄호 문자열들이 3가지 조건에 부합한지를 판단하는 문제
3가지 조건은 1) 열린 괄호는 동일한 괄호 모양으로 닫혀야 함, 2) 열린 괄호는 올바른 순서로 닫혀야 함, 3) 닫힌 괄호는 동일 괄호 모양의 열린 괄호가 있어야 함(1번과 동일 내용)

Stack 이용

var isValid = function(s) {
    const pairs = {
        "[" : "]",
        "{" : "}",
        "(" : ")",
    }
    let stack = []
    const keyList = Object.keys(pairs)

    for(let i = 0; i < s.length; i++){
        if(keyList.includes(s[i])){
            stack.push(s[i])
        }else{
            if(s[i] === pairs[stack[stack.length-1]] ) {
               // ')' 와 pairs의 데이터 비교
               stack.pop()     
            }
            else return false 
        }
    }
        return stack.length ? false : true
};

• s는 '( ) [ ] { }' 만 포함하기 때문에 동일형태의 괄호들끼리 짝을 지어 변수를 선언한다.
  -> Object.key = value가 되는 속성을 활용하는 것이다.
  따라서, pairs[ [ ] = "]", pairs[ { ] = "}", pairs[ ( ] = ")" 가 된다.
• pairs의 key값들만 추출하여 배열 형태로 가공한다 -> keyList
• s 문자열이 열린괄호(keyList 중 하나)로 일 때에는, stack 배열에 해당 문자열을 push()하고 닫힌괄호일 때에는 stack에 저장된 데이터가 pairs의 key값에 해당하는 value인지를 체크한 뒤 일치하면 stack의 마지막 데이터를 pop(), 일치하지 않으면 false를 반환한다.
• s의 길이만큼 반복하면 stack이 존재하거나 비어있게(3가지 조건에 부합) 된다.

Stack ?

스택(Stack)알고리즘은 우리 일상에서도 흔히 찾아볼 수 있다. 웹 브라우저의 '뒤로가기' 버튼을 눌러 이전 화면으로 돌아갈 때, 작성하던 텍스트를 'back space' 로 지울 때와 같은 상황이다.

stack이란

스택(Stack)은 탑을 세우듯 세로로 데이터를 쌓아올리는 자료구조이다. 메모리에 새로 유입되는 데이터가 맨 위(이전 데이터의 마지막 이후)에 쌓이고, 삭제되는 데이터는 맨 위부터(후순위로 유입된 데이터) 실행되어 순서가 존재하기 때문에 'index' 라는 개념을 사용한다. 따라서 stack은 Last In, First out -> 나중에 들어온 게 먼저 나간다

stack의 시간 복잡도

데이터의 삽입/삭제/검색 할 때, 각각 O(1)/O(1),O(n)의 시간이 소요된다.

삽입의 경우, push() 메서드를 사용하며 맨 마지막 위치에 유입되기 때문에 단한번 'O(1)' 의 행위만 있으면 된다. 이와 유사하게 pop() 메서드를 통해 탑의 맨 위 위치에서 삭제되므로 역시 O(1)의 시간 복잡도를 가진다.

검색을 할 때에는 삽입/삭제와 다르게 O(n)의 시간이 소요되는데, 그 이유는 순서가 존재하는 stack의 구조상 정확한 위치(index)를 알지 못하면, 처음(index=0)부터 마지막(index= n.length-1)까지 다 훑어봐야하기 때문이다. 로직에서 가장 많이 볼 수 있는 for문이 stack의 검색 알고리즘을 구현한 것이다.