[TIL] Cramer’s rule

위와 같은 행렬이라고 할 때, 이 행렬의 열은 벡터가 변환시 어떻게 변해가는가를 알려주는 역할을 합니다. 각 열은 변환 기저 벡터가 변환 후 도달하는 곳을 알려주는 것입니다
먼저 주어진 결과 벡터인 [-4; -2]가 행렬의 열들의 선형 결합임을 먼저 알아야 합니다. 결과 벡터[-4; -2]는 x[$\hat{i}$의 변환]+ y[$\hat{j}$의 변환]과 같습니다.
이 과정에서는 행렬식이 0이 아닌 경우를 다룹니다.

1. 내적을 이용해 해를 구할 수 있을까?
   미지의 입력 벡터 x 좌표는 첫번째 기저 벡터 [1; 0]와의 내적으로 얻어지고, 마찬가지로 y좌표는 두 번째 기저 백터 [0; 1]와의 내적으로 얻어질 것입니다. 그러면 이런 생각을 할 수도 있을 것 같습니다. 기저 벡터가 변환되어 만들어진 미지 벡터의 변환 벡터의 내적 역시 x좌표와 y좌표가 될 것이라고 생각을 할 수도 있을 것입니다.
   하지만 이는 전혀 사실이 아닙니다. 대부분의 벡터들에 대해 선형 변환 이전과 이후의 내적은 매우 다르기 때문입니다.
   내적이 보존되는 변환은 상당히 특수한 경우이며, 이 경우는 '직교 변환'이라고 합니다. 이 직교변환에서는 기저벡터끼리 수직인 상태이며, 길이까지 유지되는 상태를 말합니다.
   직교 변환의 경우에는 내적이 보존되기 때문에, 구하려는 벡터와 모든 기저 벡터 사이의 내적은 같고, 그렇기 때문에 첫번째 열과 결과 벡터[1; 2]의 내적은 x, 두번째 열과 결과 벡터[1; 2]의 적은 y가 될 것입니다.

2. 행렬식의 발상을 이용해보자
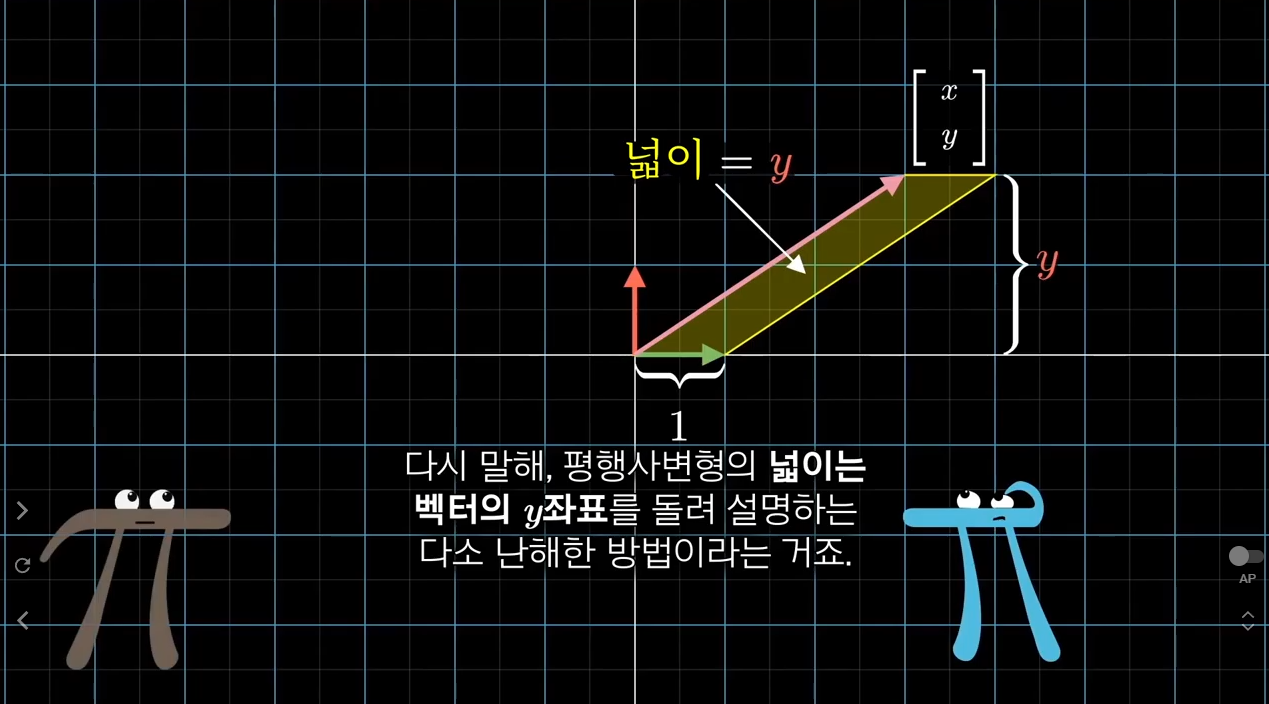   행렬식에서 첫번째 기저 벡터 $\hat{i}$과 미지수 벡터 [x; y]를 가지고 평행사변형을 그립니다. 이 평행사변형의 넓이는 벡터의 y좌표에 의해 결정됩니다. 다시 말해서, 평행사변형의 넓이는 벡터 y 좌표를 돌려 설명하는 것과 같습니다.
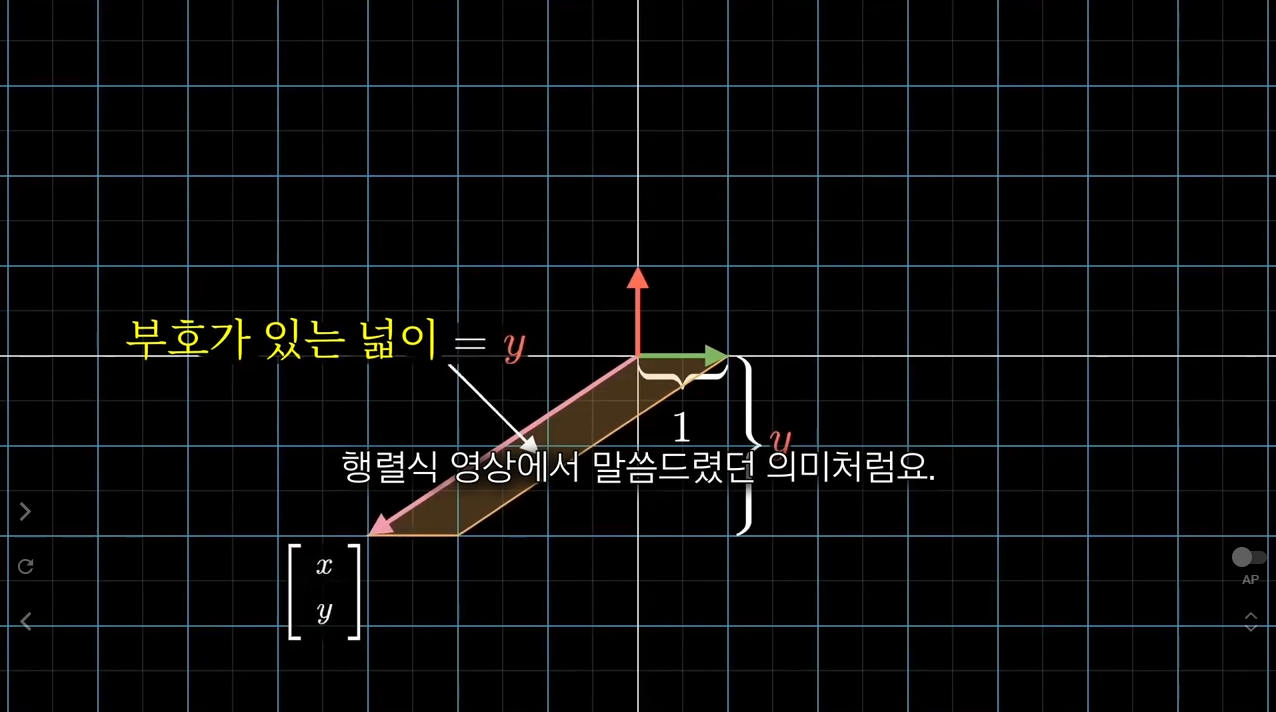   더 정확히는, 저 넓이는 부호가 존재합니다. 이말은 즉슨, y 좌표가 (-)일 때, 이 평행사변형의 넓이도 (-)가 된다는 것입니다.
   반대로 두번째 기저벡터인 $\hat{j}$으로 생성되는 평행사변형은 넓이가 x좌표가 됩니다.
   이를 3차원 공간으로 일반화시키면, 밑 면이 $\hat{i}$과 $\hat{j}$으로 생성되는 평행육면체도 생각해볼 수 있습니다. 밑면이 $\hat{i}$과 $\hat{j}$의 넓이는 1이고, 높이가 z므로, 부피는 z좌표가 됩니다. 마찬가지로, x, y에 대입하여 적용할 수 있습니다. 여기서 주의해야 할 점은 벡터의 순서가 중요하다는 것입니다.
   행렬 변환을 적용했을 때, 평행사변형의 넓이는 유지되지 않고 더욱 커지거나 줄어들게 됩니다. 모든 넓이는 변환 행렬의 행렬식의 배만큼 일정하게 증가하게 됩니다.
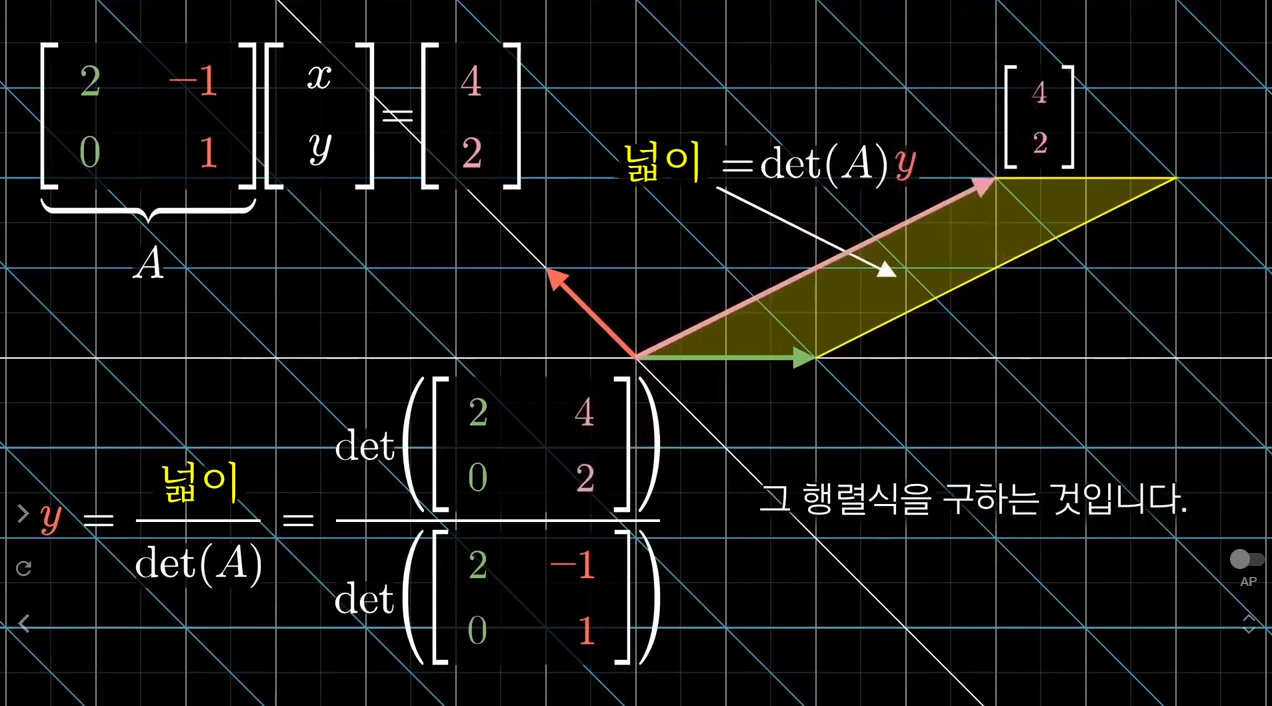   원래 넓이가 미지 벡터 y 좌표였으니, 변환 후 넓이는 행렬식 x y좌표가 될 것입니다. 따라서 우리는 y 값을 구할 수 있습니다. y는 결과값의 (변환 후 평행사변형의 넓이)를 (전체 변환의 행렬식)으로 나눈 값입니다.
   이때, 우리는 [4; 2]가 어디로 도달하는지를 알기 때문에 새로운 행렬을 만들어야 합니다. 변환 벡터의 첫번째 열벡터는 그대로 놓고, 두번째 열벡터에는 결과 벡터 [4; 2]를 집어 넣습니다.
   같은 발상을 x에도 적용을 해봅니다. 평행사변형의 넓이는 첫번째 열에는 결과 벡터를 넣고, 두 번째 열에는 원래 열벡터를 넣어서 구할 수 있습니다.