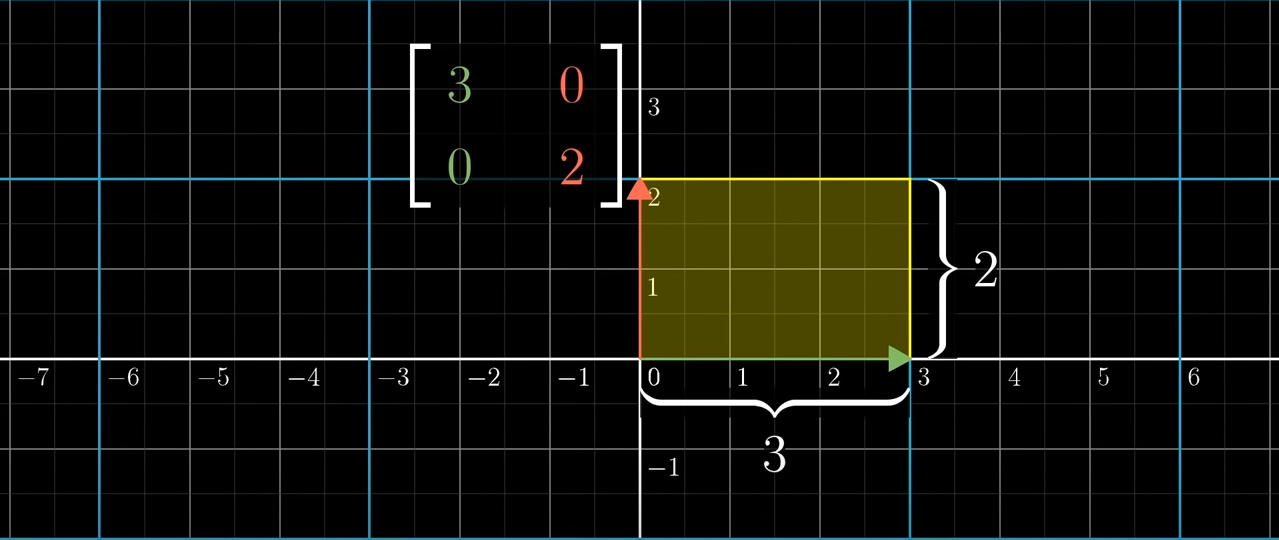
선형변한을 배우게 되면 어떤 것들은 공간을 확대시키기도 하고, 어떤 것들은 공간을 축소시키기도 합니다. 이러한 변환을 이해하는데 꽤 도움이 되는 방법중 하나가 바로 물체를 얼마나 확장하는지, 축소시키는지 확인해보는 것입니다.
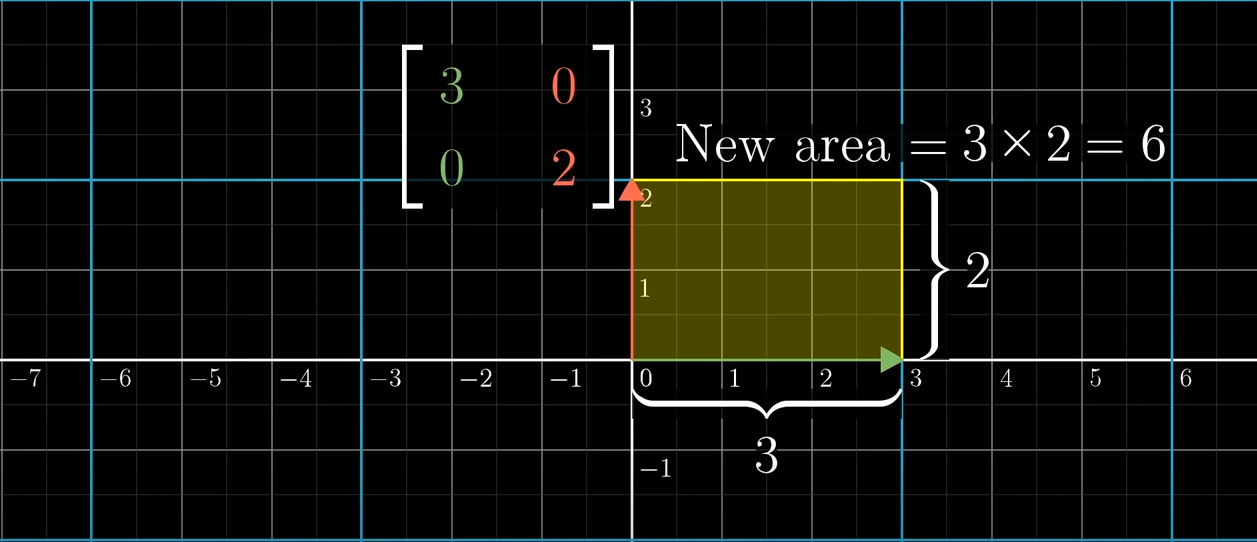
기저 벡터인 와 으로 이루어진 사각형이, 위의 행렬 변환을 통해 2x3 직사각형이 되었습니다. 즉, 처음엔 area가 1로 시작했는데 나중엔 6으로 증가를 한 것이지요. 우리는 이 선형변환은 영역을 6배 확장시킨다고 할 수 있습니다.
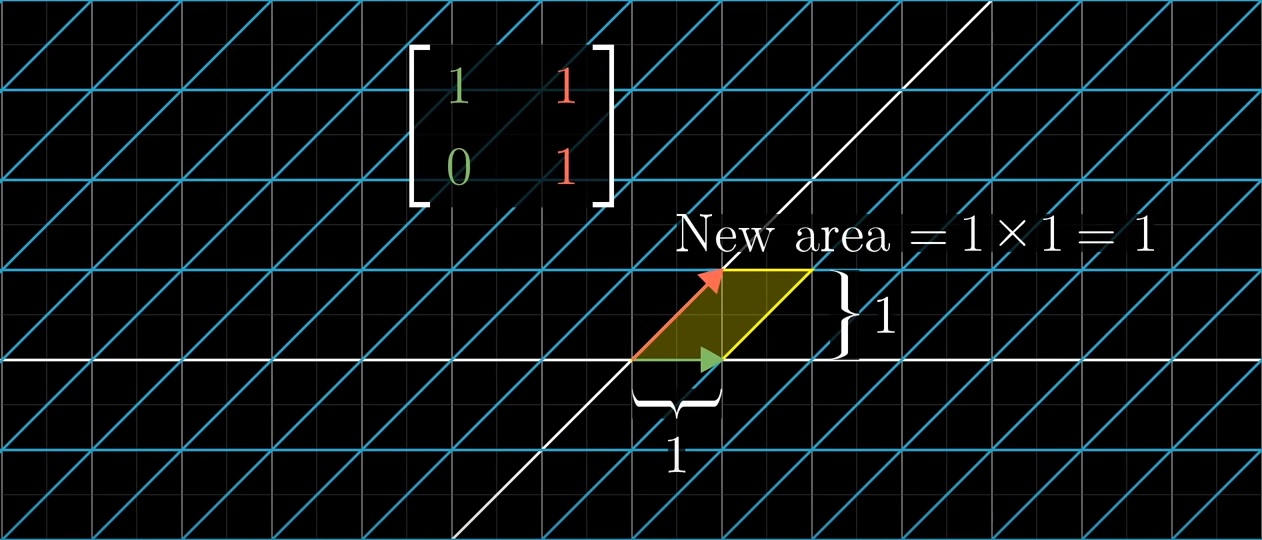
그럼 전단(shear) 행렬 변환은 어떻게 될까요? 와 로 이루어진 단위 정사각형이 평행사변형이 되어서, 여전히 area가 1입니다.
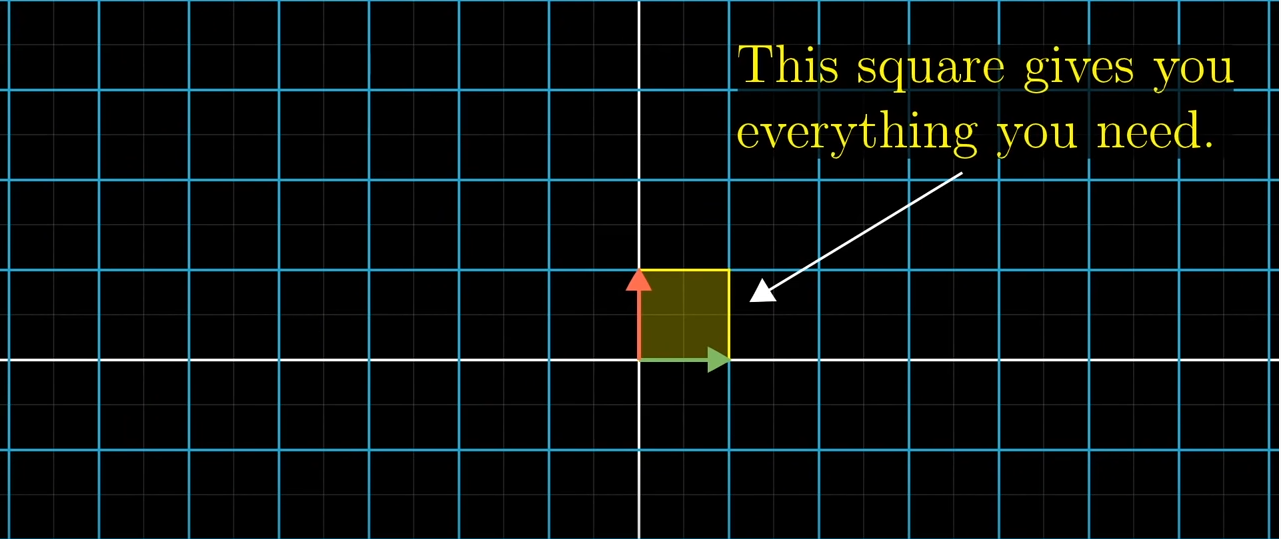
사실 저희는 이 와 로 이루어진 단위 정사각형의 영역이 얼마나 변하는지만 알면 공간상 어떤 지역이 어떻게 변할지를 예측할 수 있게 됩니다. 좌표는 평행하고 균등한 거리를 유치한채 변하기 때문에 다른 정사각형들도 비례하여 변하기 때문이죠
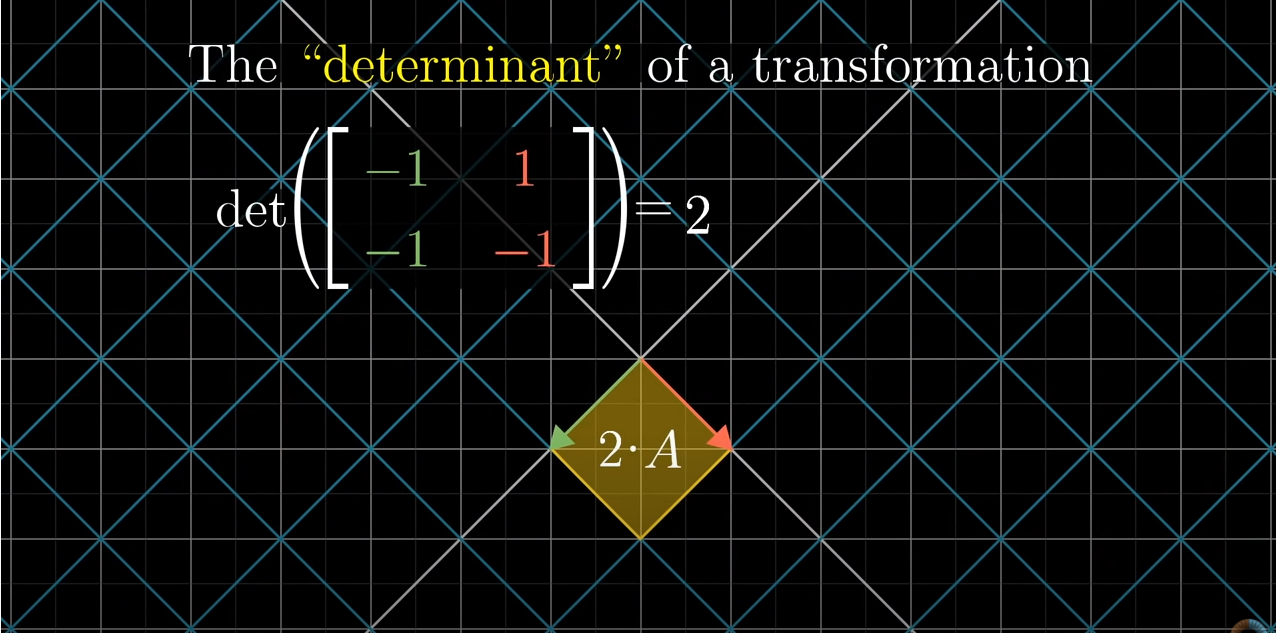
determinant(행렬식)은 선형 변환에 의한 넓이의 변화를 나타내는 factor로서, determinant가 2이면 넓이는 2배 만큼 증가합니다. 마찬가지로 행렬식이 0.5라면 넓이는 0.5배 감소할 것입니다.
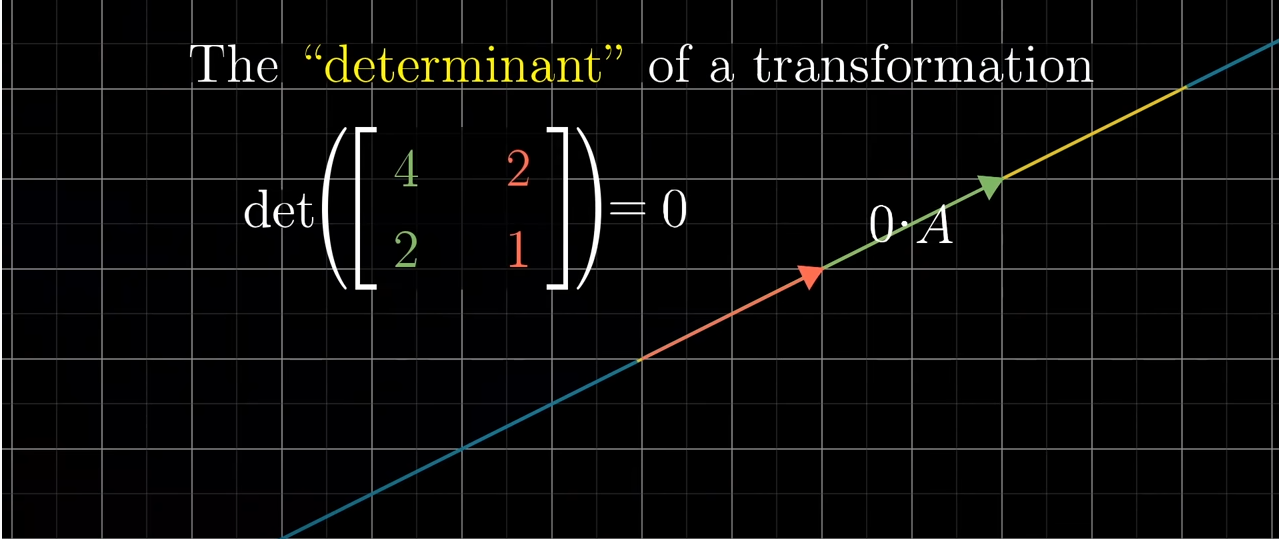
특별한 것은, 행렬식이 0일 때 입니다. 2차원 변환의 행려려식이 0이라면 모든 공간이 찌부러져서 선이 될수 있습니다. 심지어 한 점이 될 수 있습니다. 그러면 넓이는 0이 될 것입니다. 그래서 주어진 행렬식이 0인지 확인하는 것은 중요합니다. 계산할 수 있는지 없는지를 가르쳐주기 때문이죠.
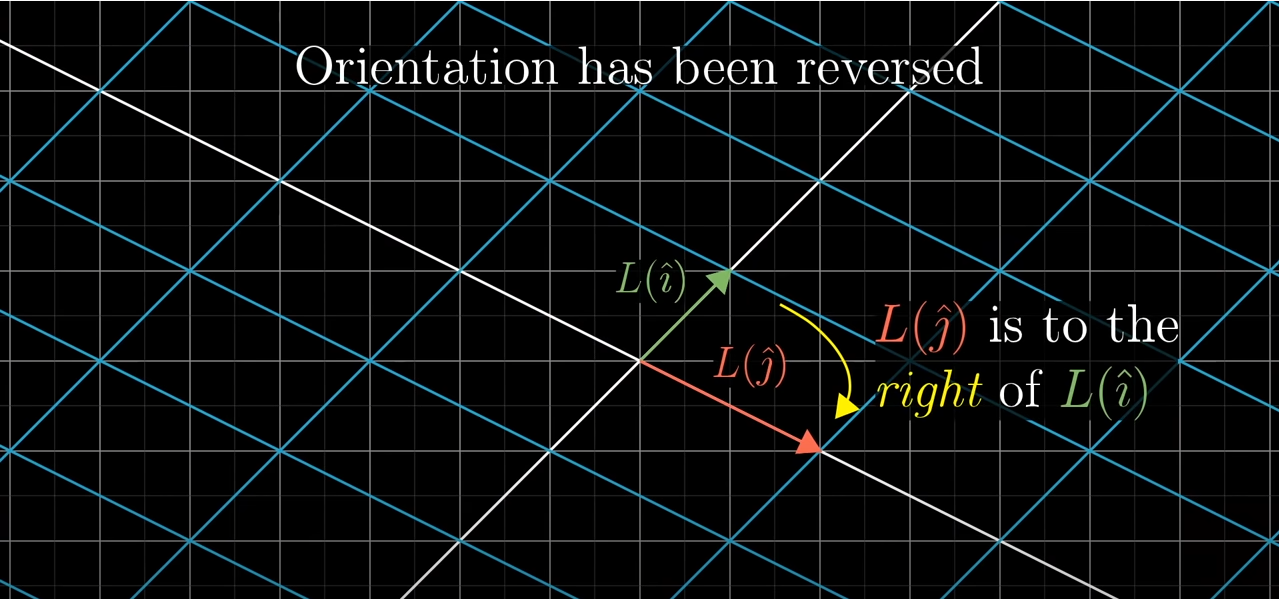
사실 행렬식은 음수를 허용하기도 합니다. 음수인 행렬식은 무엇을 의미할까요? 시각적으로 보면 음수인 행렬식은 공간이 뒤집혀진 느낌을 주기도 합니다. 이걸 확인할 수 있는 방법이 와 의 위치입니다. 의 위치가 위치의 오른쪽에 있다면, 행렬식이 음수인 것을 의미합니다.
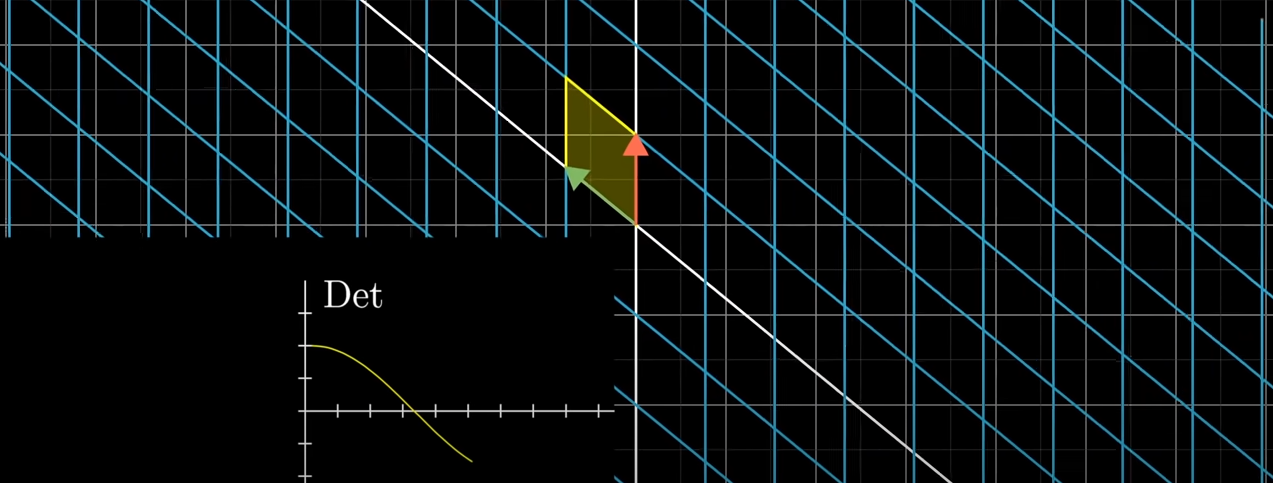
연속된 관점으로 보면 와 가 점점 가까워지고, 와 가 완전히 한 선을 이루게 되면 행렬식이 0입니다. 그리고 이 계속해서 움직이면 행렬식은 음수가 되어버립니다
그럼 3차원 공간에서는 어떻게 될까요? 3차원 공간에서는 부피의 스케일링에 대해 보여줍니다.
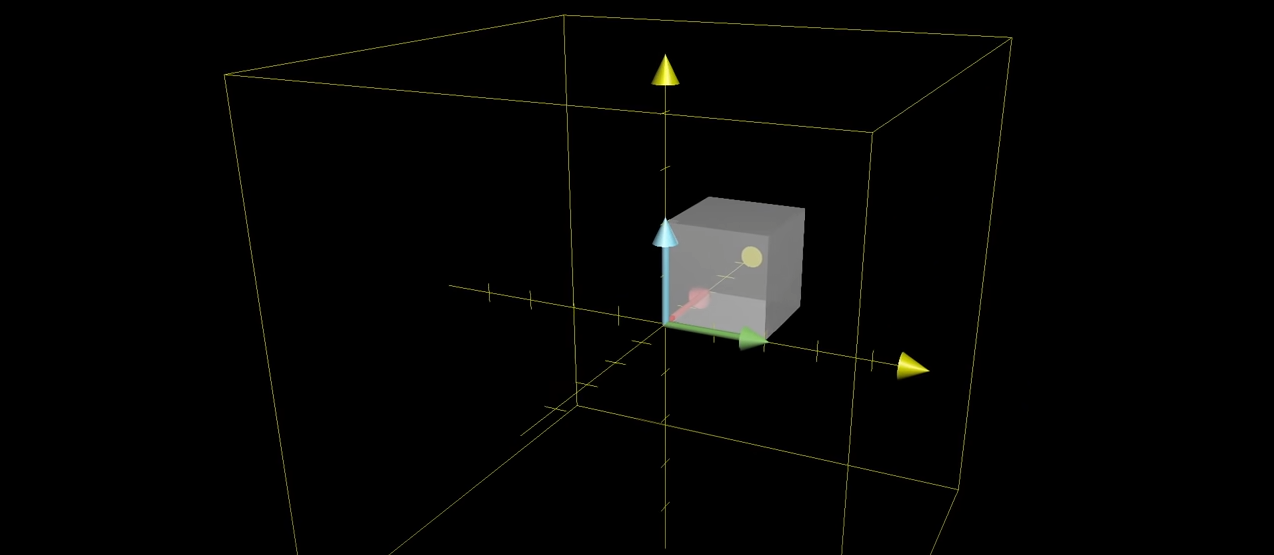
2차원에서는 기저 벡터들의 넓이 변화를 봤던 것 처럼, 3차원에서는 기저 벡터 , , 의 부피를 살펴봅니다. 3차원에서 행렬식이 0이라는 것은, 부피가 찌부러져서 평면이나 선, 극단적으로 점이 된다는 의미입니다.
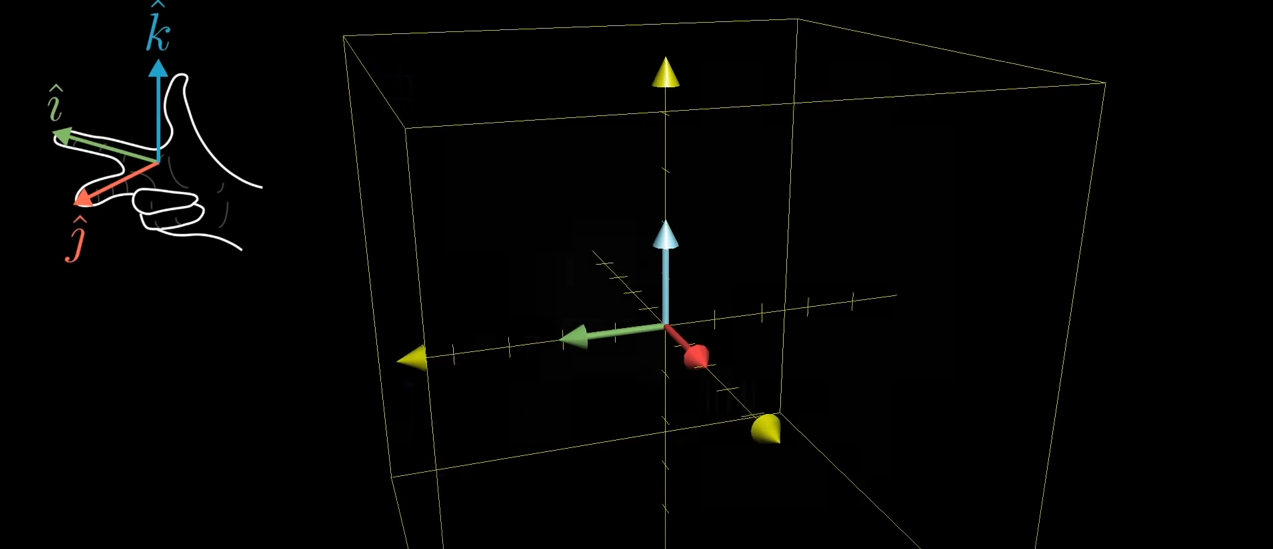
그럼 3차원에서, 행렬식이 음수인 경우는 어떻게 된 것일까요? 3차원 공간에서는 오른손의 법칙이 있습니다. 여전한 행렬 변환에서도 이 규칙이 변하지 않으면, 공간이 뒤집혀진 것이 아닙니다. 하지만 변환 이후에 왼손으로 바꿔야 하는 경우에는 방향이 반전된것이고, 이 때 행렬식은 음수입니다.
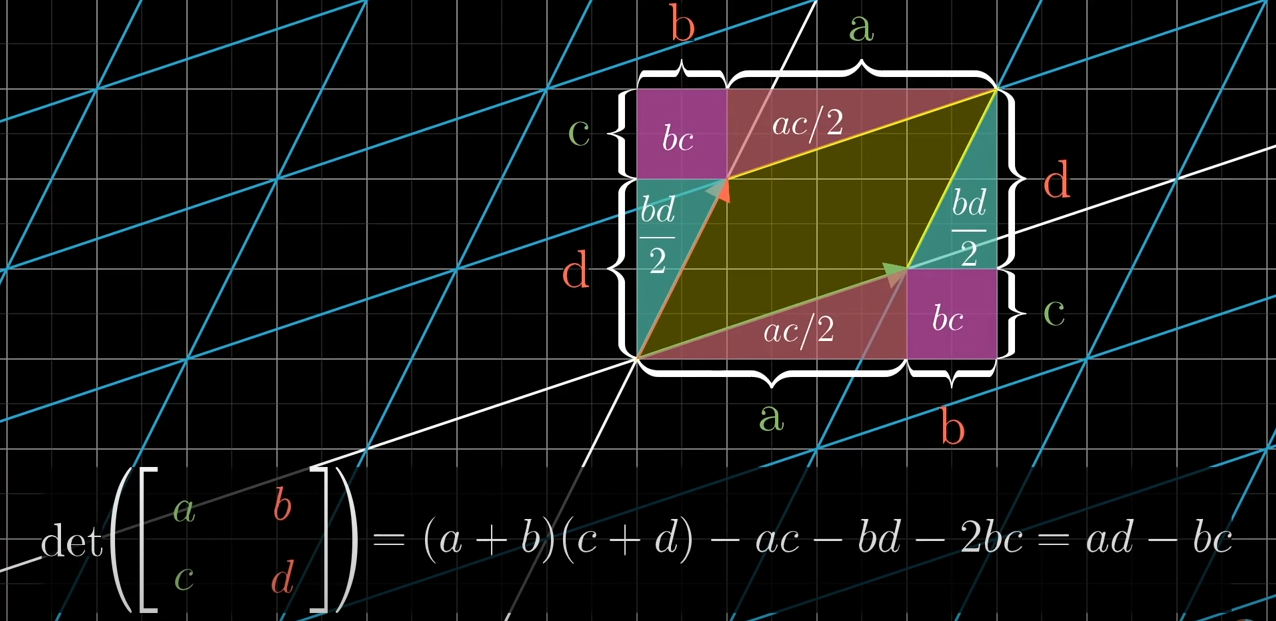
2차원에서 행렬식의 공식은 위와 같이 구해집니다. a, d는 직사각형의 크기 가로와 세로의 길이이고, b, c가 알려주는 것은 이 사각형이 얼마나 대각선으로 늘려지거나 찌그러지는 지를 말해줍니다.
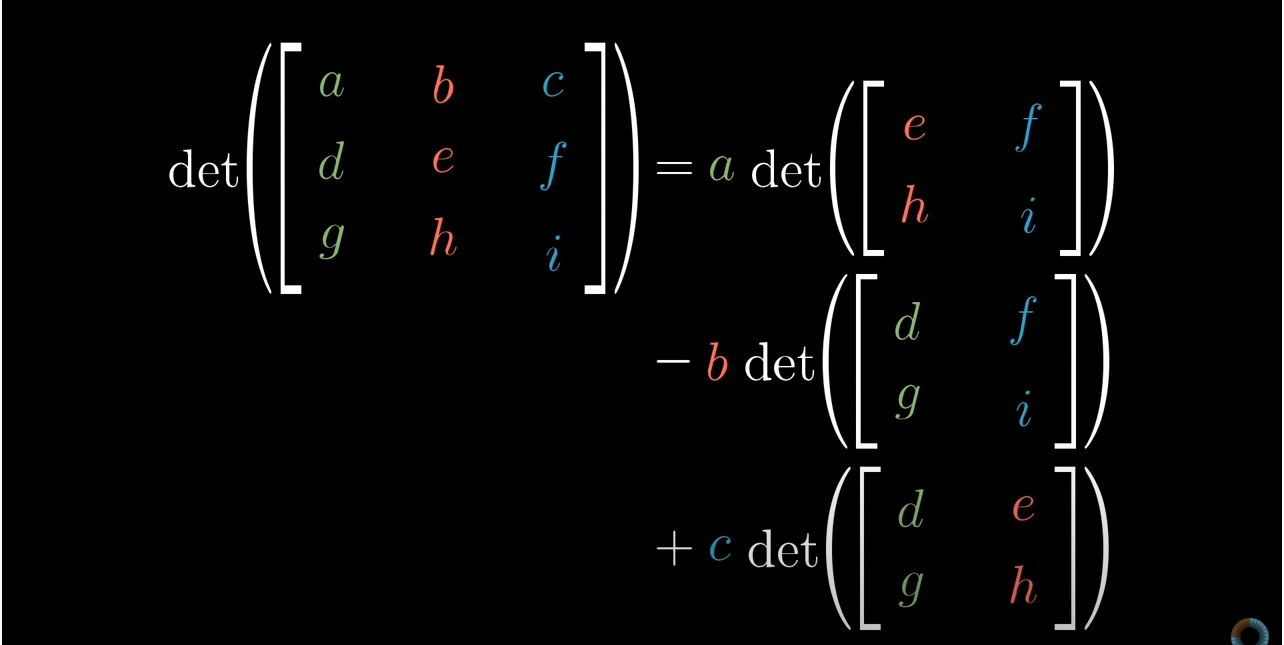
3차원 행렬의 공식은 위와 같습니다. 강의에서는 행렬의 공식이 그리 중요하다고 하진 않습니다.