요즘 KMP와 이분 매칭을 공부하고 있다.
이 알고리즘 자체가 이해하기 어렵고 복잡한 알고리즘이다 보니, 문제 난이도 자체가 높아 백준 티어가 쭉쭉 올라간다.
그러는 와중 어제 플레 4를 찍어서 그 기념으로
BOJ 1014 - 컨닝 문제를 다뤄보겠다.

BOJ 1014 - 컨닝 링크
(2022.07.28 기준 난이도 P4)
(치팅하지 맙시다!)

문제

N행, M열 크기의 직사각형 교실에 컨닝을 못하는 배치로 하여금 최대한 앉힐 수 있는 학생 수

알고리즘

"이분 매칭" 으로 접근하여 해결하였다.
이분 매칭에 대한 설명은 구글에 검색하면 설명 잘 되어 있는 글을 많이 찾을 수 있다.
나는 개인적으로 https://yjg-lab.tistory.com/209 이 글로 이분 매칭에 대한 이해를 확실히 했었다.

풀이

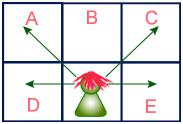
일단 컨닝을 할 수 있는 방향부터 알아보자
나의 위치가 (i, j)이면 A (i - 1, j - 1), C (i - 1, j + 1), D (i, j - 1), E (i, j + 1)인 위치의 시험지를 컨닝할 수 있다.
잘 살펴 보면, 나랑 다른 열인 위치라는 것을 알 수 있다.
이를 풀어서 말하면 홀수 열에 있는 학생은 짝수 열 시험지를, 짝수 열에 있는 학생은 홀수 열 시험지를 컨닝할 수 있다는 것이다.
그래서 홀수 열과 짝수 열에 있는 학생들을 컨닝할 수 있는 조건으로 이분 매칭시켜 나오는 쌍의 수를 앉을 수 있는 자리의 수에서 빼면 된다.

주의사항

허접한 그림판 실력 죄송합니다..
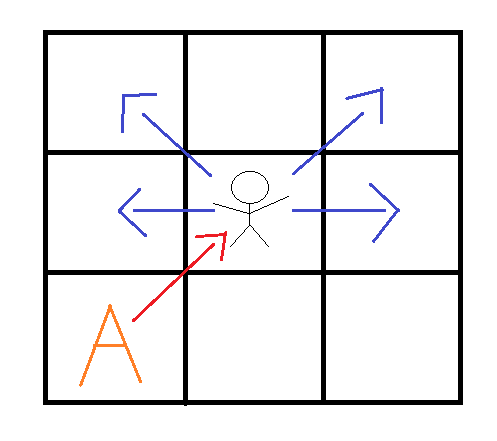
위에 풀이 대로 컨닝 가능한 4방향(파란색 화살표)으로 이분 매칭을 시킨다고 생각해보자.
그럼 만약 A 위치에 있는 학생은 빨간색 화살표 방향으로 가운데 학생의 시험지를 컨닝을 못하는 것일까? 그건 아니다.
컨닝이 어느 방향이든 이루어지면 안되기 때문에 왼쪽 아래, 오른쪽 아래 방향 [(i + 1, j - 1), (i + 1, j + 1)]을 포함한 6방향으로 탐색을 해줘야 한다.

코드

import sys; input = sys.stdin.readline

def bip_match(n, m): # 이분 매칭
    for nn, mm in [(n, m - 1), (n, m + 1), (n - 1, m - 1), (n - 1, m + 1), (n + 1, m - 1), (n + 1, m + 1)]: # 6방향으로 탐색
        if 0 <= nn < N and 0 <= mm < M and not visited[nn][mm] and seat[nn][mm]:
            visited[nn][mm] = True
            if connect[nn][mm] == [-1, -1] or bip_match(connect[nn][mm][0], connect[nn][mm][1]):
                connect[nn][mm] = [n, m]       
                return True
    return False

for _ in range(int(input())):
    N, M = map(int, input().split())
    matrix = [input().strip() for _ in range(N)]
    
    seat = [[False] * M for _ in range(N)] # 앉을 수 있는 자리인지 저장하기 위한 행렬
    answer = 0
    for n in range(N):
        for m in range(M):
            if matrix[n][m] == '.':
                seat[n][m] = True
                answer += 1 # 앉을 수 있는 자리이면 seat 갱신해주고 answer에 자리 수 저장
                
    connect = [[[-1] * 2 for _ in range(M)] for __ in range(N)] # 각 자리 별 연결 위치를 저장하는 행렬
    for n in range(N):
        for m in range(0, M, 2): # 여기서 짝수로 해도 되고 홀수로 해도 된다. 물론, 둘 다 하면 안된다.
            if seat[n][m]:
                visited = [[False] * M for _ in range(N)]
                if bip_match(n, m):
                    answer -= 1 # 이분 매칭이 될 때마다 앉을 수 있는 자리가 하나씩 줄어든다
                    
    print(answer)

여담

이 문제랑 BOJ 11014 - 컨닝 2 는 같은 문제이다.
다른 점은 행렬 크기 정도?
1014랑 11014 둘 다 같은 코드로 제출해도 통과한다.