저번 글을 보면 KMP와 이분 매칭을 공부 중이라고 했었는데, 지금도 그렇다.
그래서 이번엔 KMP 알고리즘을 다루는 BOJ 1787 - 문자열의 주기 예측 문제를 풀이해보겠다.

BOJ 1787 - 문자열의 주기 예측 링크
(2022.08.02 기준 P2)
(치팅은 놉! ❌)

문제

모든 위치에서, 가장 긴 주기(그 위치에서 끝나는 문자열에서의 접두사와 접미사가 같으면서 제일 가장 짧은 길이를 위치 값에서 뺀 값)들의 합

알고리즘

"KMP"에서의 실패 함수를 사용하여 문제를 풀었다.
왜냐 하면, 접두사와 접미사가 같을 때의 그 길이를 어찌어찌 사용해야 하기 때문.

풀이

일단, 실패 함수를 잘 이해하고 오자.
그 다음에 이 풀이를 볼 것

(지금 컴퓨터 포맷해서 그림판 밖에 없어요.. ㅠㅠ)
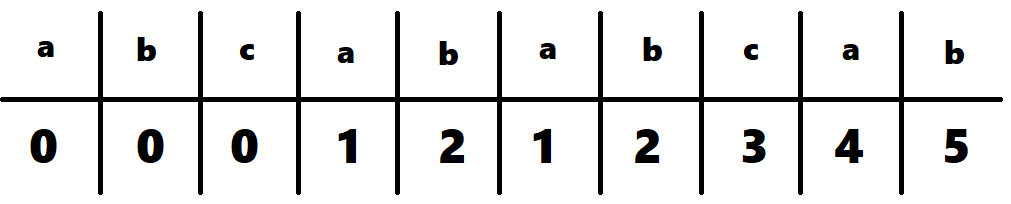
만약 문자열이 abcababcab 라면
pi는 [0, 0, 0, 1, 2, 1, 2, 3, 4, 5]가 될 것이다.

그리고 문제대로 각 위치에서 주기를 예측한다고 하면, 일단 위치 10 (idx는 9) 에서의 주기를 예측해보자.
조건인 '단, 이러한 추정에서 뒤쪽 문자열이 앞쪽 문자열보다 길면 안 된다.' 대로 앞 문자열과 뒤 문자열을 나누어 보면

a b c a b|a b c a b
a b c a b a|b c a b
a b c a b a b|c a b
a b c a b a b c|a b
a b c a b a b c a|b

이렇게 나눌 수 있다.
2, 3, 5번째는 뒤 문자열이 앞 문자열의 접두사가 될 수 없기 때문에 주기가 될 수 없다. 1번째는 pi[9] = 5 처럼 최대 길이 만큼 잘린 것을 볼 수 있고 주기는 5가 된다.
자, 이제 중요한 것은 4번째이다.

1번째를 보면 알 수 있듯이 앞 5개와 뒤 5개는 같다. (pi[9] = 5)
4번째에선 뒤 문자열이 2개인데 이는 1번째의 접두사에서의 뒤 2개랑 같은 것을 알 수 있다.
(빨간색 박스의 파란색 박스)
여기서 pi를 보면 뭔가 보이지 않는가?
위치 5 (idx는 4) 에서의 최대 일치 길이가 2라는 것이 보인다.
이는 pi[9] = 5 였고 pi[5 - 1] = 2 라는 것이고
pi[pi[i] - 1] 를 구한다는 것이다.
물론, 값이 0이 되기 전까지다.

length = []
while pi[i] and not i < 0:
    length.append(pi[i])
    i = pi[i] - 1
if length:
    length = min(length)
else:
    length = 0

이런 느낌으로?

길이가 나오면 그 길이 만큼 위치 값에서 빼주면 그 위치에서의 가장 긴 주기가 나온다.
이 과정들을 모든 위치에서 구해주고 합을 출력하면 된다.

주의사항

길이가 길어질수록 구했던 값을 다시 구하는 횟수가 늘고 결국 시간초과가 날 것이다.
그러므로 메모이제이션 기법을 사용하자.

코드

from math import inf

def dfs(i): # 풀이에서 말했던 pi[pi[i] - 1] 를 차례대로 찾아가는 함수
    if i < 0 or not pi[i]: # 인덱스가 0보다 작아지거나 pi[i] 가 0이면 멈춘다.
        return inf
    if dp[i] > -1: # 메모이제이션 기법으로, i에서의 결과를 전에 구한 적 있으면 다시 꺼내 쓴다.
        return dp[i]
    dp[i] = min(pi[i], dfs(pi[i] - 1)) # 가장 짧은 길이를 구해 dp[i]에 저장한 다음, 반환
    return dp[i]

n = int(input())
S = input().strip()

# 실패 함수
pi = [0] * n
i = 0
for j in range(1, n):
    while i and S[i] != S[j]:
        i = pi[i - 1]
    if S[i] == S[j]:
        i += 1
        pi[j] = i

dp = [-1] * n
answer = 0
for i in range(n):
    result = dfs(i)
    if result < inf: # inf가 나오면 길이를 구하지 못했다는 것이므로 (주기가 없다는 것이므로) 패스
        answer += i + 1 - result # i는 인덱스이므로 실제 위치 값은 i + 1. 그러므로 (i + 1 - 최단 길이)를 합에 더해줘야 한다.
print(answer)

여담

설명이란, 참 어려운 것 같다.
잘 설명하고 싶은데 ㅠㅠ
블로그를 꾸준히 하면서 설명하는 실력도 키워가야 겠다.

그리고 python 업데이트? 때문에 in 연산자가 시간복잡도가 O(n)으로 줄었다고 한다. (맞나..?)
이 때문에 파이썬에서의 kmp 문제는 굉장히 쉬워졌겠지?
그래서 그런지 지금 백준에서의 간단한 kmp 문제들의 난이도가 낮아지고 있는 것 같다...
운영자의 '언어별 난이도 분리' 같은 조치가 필요해 보인다. 그냥 여담 끝!