쥐를 잡자 쥐를 잡자 찍찍찍
(잡아라 쥐돌이 재밌었는데..)

BOJ 1087 - 쥐 잡기 링크
(2022.11.07 기준 P4)
(치팅하면 집에 쥐 나옴)

문제

N마리의 로봇 쥐와 그 쥐들의 각 위치는 t초일 때 (px+vx*t, py+vy*t)이다.
회전이 불가능한 축에 평행한 길이 L인 정사각형 모양의 우리로 쥐들을 잡는다고 했을 때, 한 번에 모든 쥐를 잡을 수 없는 가장 큰 L

알고리즘

쥐들의 거리는 t에 따라 아래가 볼록한 함수 모양을 띈다. 극솟값을 갖는 t를 찾는 것이므로 삼분 탐색

풀이

일단, 정확하게 어떤 값을 구하는지 알아야 한다.
정사각형 모양의 우리는 최대로 커야 한다. 그리고 회전이 불가능하고 축에 평행하다.
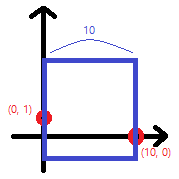
만약 두 마리의 쥐의 좌표가 [(10, 0), (0, 1)] 이라면? L의 최댓값은 10이다.

결국은 t초 때의 함수값은 쥐들의 좌표 중 x 최대 차이와 y 최대 차이 중 더 큰 값이 된다.
그렇다면 x에 따라 정렬하고 처음 쥐와 마지막 쥐의 x 차이. 그리고 y에 따라 정렬하고 처음 쥐와 마지막 쥐의 y 차이. 이 두 값 중 큰 값을 선택하면 되는 것이다.

(사실 naive하게 모든 쥐 간의 x와 y의 차이를 구해도 AC를 받긴 함)

이제 삼분 탐색을 하면 된다.
t의 양 끝은 어떻게 잡아야 할까?
이 문제의 쥐의 시작 위치와 속도의 절댓값은 1000 이하의 정수. 그러면 두 쥐 사이의 거리가 어떻든 2000초 안에 가장 가까워지는 시간이 있다는 것이다.
그러므로 양 끝은 0과 2000으로 잡자.

코드

import sys; input = sys.stdin.readline

# 최대한 큰 정사각형 우리를 만들어야 하므로
# 좌표 x 차이나 y 차이가 제일 큰 쥐들로 하여금 우리 크기를 맞추면 된다.
def f(t):
    points = [] # 쥐들의 좌표
    for px, py, vx, vy in mouse:
        points.append([px + vx * t, py + vy * t]) # 시간에 따른 좌표 저장

    # x 정렬
    points.sort()
    result = points[-1][0] - points[0][0] # 제일 큰 좌표 x 차이

    # y 정렬
    points.sort(key = lambda x: x[1])
    result = max(result, points[-1][1] - points[0][1]) # 제일 큰 좌표 y 차이를 비교하여 저장 후 반환
    return result

N = int(input())
mouse = [list(map(int, input().split())) for _ in range(N)]

# 시작 위치와 속도의 절댓값은 1000 이하의 정수.
# 그러므로 2000초 내로 제일 가까운 거리가 무조건 나온다.
start = 0; end = 2000

# 500번 정도 돌리면 소수점 오차가 10^-9가 맞춰진다.
for _ in range(500):
    mid_1 = (start * 2 + end) / 3
    mid_2 = (start + end * 2) / 3
    if f(mid_1) <= f(mid_2): # 함수값에 따라 범위 조정
        end = mid_2
    else:
        start = mid_1

print(f(start))

여담

처음엔 정렬할 생각을 못했다. naive하게 풀고 AC를 받은 후 다른 분들 제출 코드 보고 깨달았다.
좌표에 대한 문제는 파고들면 들수록 어려운 것 같다.