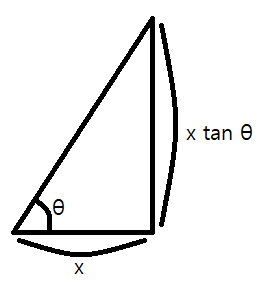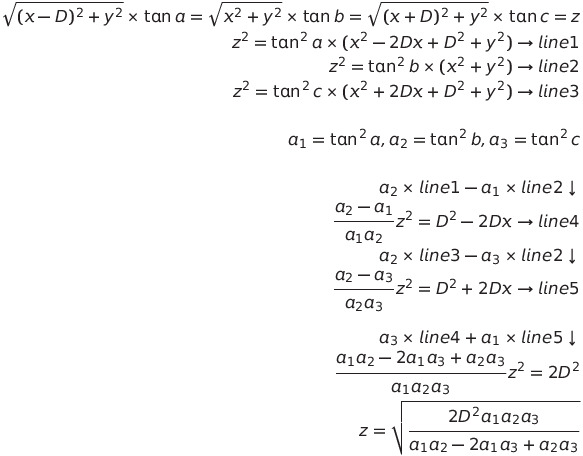직전에 올린 기하학 + 연립방정식 문제에 이은 두번째 문제는 바로 3D 기하학 + 삼각연립방정식

BOJ 2761 - 모형 로켓의 높이 링크
(2022.11.04 기준 G1)
(치팅하면 삼각자로 맞음)

문제

관측자 3명이 간격 D를 둔 채 일직선 상에서 로켓을 측정했을 때의 각도가 a, b, c라 하면, 로켓의 높이 출력

알고리즘

예상하다시피 tan 삼각방정식을 이용한 연립방정식을 풀면 된다.

풀이

문제 지문이 모호하다.
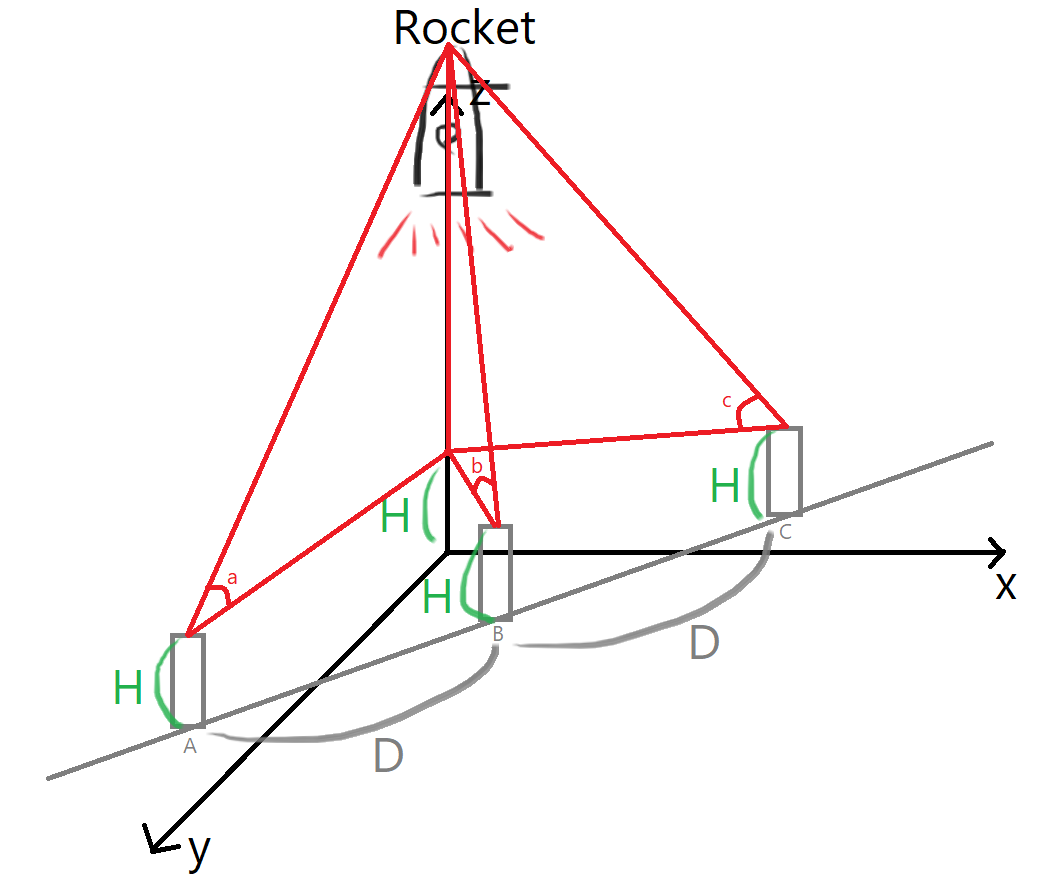
그림으로 쉽게 표현하면

이런 상태인 것이다.

그렇다면 로켓이 있는 z축을 중심으로 관측자들의 직선과 x축이 평행하게끔 좌표계를 회전한다면
각 관측자들은 [(x - D, y, H), (x, y, H), (x + D, y, H)]에 있게 된다.
편하게 관측자들의 z좌표를 0이라 생각하고 높이를 구한다음 나중에 H를 더하자.

밑변의 길이와 각도를 알면 높이를 알 수 있다.
로켓은 (0, 0, answer)에 있고 z = answer - H 라고 한다면, z는 곧 각 관측자들과의 밑변 거리와 각도로 하여금 구해지는 높이가 된다.
그러면 세 삼각방정식이 나오는데.. 정리를 해서 풀면 된다.
(2연속 수학 문제)

z를 구하면 H를 더해 반올림하여 출력하자.

코드

# 풀이에 있는 식 정리를 참고
import sys; input = sys.stdin.readline
from math import tan, radians

D, H = map(float, input().split())
while True:
    a, b, c = map(float, input().split())
    if not a:
        break

    # 필요한 tan θ 제곱
    a1 = tan(radians(a)) ** 2
    a2 = tan(radians(b)) ** 2
    a3 = tan(radians(c)) ** 2
    print(format(((2 * D ** 2 * a1 * a2 * a3) / (a1 * a2 - 2 * a1 * a3 + a2 * a3)) ** 0.5 + H, '.0f'))

여담

이런 문제들은 풀어내면 짜릿한 문제인 것 같다. 왠지 모르게 내가 수학자가 된 기분이랄까