BOJ 1915 - 가장 큰 정사각형 링크
(2023.07.12 기준 G4)

문제

0이나 1로 된 배열이 주어질 때, 1로 된 가장 큰 정사각형의 크기 출력

알고리즘

DP

풀이

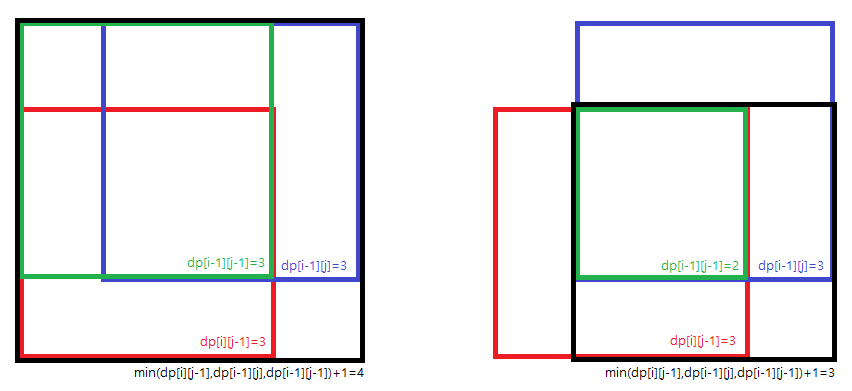
왼쪽 위부터 DP 테이블을 채워나가며, 위 그림처럼 왼쪽, 위, 왼쪽 위의 dp 값의 최솟값 + 1을 채우면 된다. (물론, 채우는 곳의 배열 값은 1이어야 한다.) 그러면 왼쪽, 위, 왼쪽 위가 어디까지 채워지는지 바로 알 수 있기 때문이다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int n, m; cin >> n >> m;
    string matrix[n]; for (int i = 0; i < n; i++) cin >> matrix[i];

    // dp[i][j] = (i, j)를 오른쪽 밑 꼭짓점으로 하는 정사각형의 최대 변의 길이
    int dp[n][m];

    for (int i = 0; i < n; i++) for (int j = 0; j < m; j++){

        // 첫번째 행이나 첫번째 열
        if (!i || !j) dp[i][j] = matrix[i][j] - '0';

        // 0이면 최대 변의 길이는 0이 된다.
        else if (matrix[i][j] == '0') dp[i][j] = 0;

        // 1이면 왼쪽, 위, 왼쪽 위의 최대 변의 길이 중 최솟값 + 1이 된다.
        else dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
    }

    // 답은 크기(넓이)이므로 최대 변의 길이를 제곱해서 출력
    int result = 0;
    for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) result = max(result, dp[i][j]);
    cout << result * result;
}

• Python

import sys; input = sys.stdin.readline

n, m = map(int, input().split())
matrix = [list(map(int, input().strip())) for _ in range(n)]

# dp[i][j] = (i, j)를 오른쪽 밑 꼭짓점으로 하는 정사각형의 최대 변의 길이
dp = [[0] * m for _ in range(n)]

for i in range(n):
    for j in range(m):

        # 첫번째 행이나 첫번째 열
        if not i or not j:
            dp[i][j] = matrix[i][j]

        # 0이면 최대 변의 길이는 0이 된다.
        elif not matrix[i][j]:
            dp[i][j] = 0

        # 1이면 왼쪽, 위, 왼쪽 위의 최대 변의 길이 중 최솟값 + 1이 된다.
        else:
            dp[i][j] = min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1

# 답은 크기(넓이)이므로 최대 변의 길이를 제곱해서 출력
print(max(max(dp[i]) for i in range(n)) ** 2)