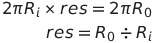BOJ 3036 - 링 링크
(2023.10.10 기준 S4)
문제
N개의 링이 순서대로 접하도록 위치해 있다.
첫 번째 링을 한 바퀴 돌렸을 때, 나머지 링의 돌아가는 바퀴 수를 기약 분수 형태로 출력
알고리즘
간단한 수학
풀이
두 원이 접하도록 놓고 한 원을 돌리면 나머지 원도 돌린 원의 돌아가는 만큼 똑같이 돈다.
원의 원주는 2πr 이다. 첫 번째의 원의 반지름을 R0이라고 하면, 한 바퀴 돌리면 돌아가는 거리는 2πR0 이다. 그러면 이에 따라 도는 원의 바퀴 수 res는
위와 같이 구할 수 있다.
출력은 기약 분수 형태로 해야 하므로, R[0]과 R[i]의 최대 공약수로 각각 나눠서 출력하면 된다.
코드
- C++
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int N; cin >> N;
int R[N]; for (int i = 0; i < N; i++) cin >> R[i];
// 2 * pi * R[i] * res = 2 * pi = R[0]
// res = R[0] / R[i]
// 기약 분수 형태로 출력해야 하므로 두 수를 최대 공약수로 나눠서 출력
for (int i = 1; i < N; i++){
int g = gcd(R[0], R[i]);
cout << R[0] / g << '/' << R[i] / g << '\n';
}
}- Python
import sys; input = sys.stdin.readline
from math import gcd
N = int(input())
R = list(map(int, input().split()))
# 2 * pi * R[i] * res = 2 * pi = R[0]
# res = R[0] / R[i]
# 기약 분수 형태로 출력해야 하므로 두 수를 최대 공약수로 나눠서 출력
for i in range(1, N):
g = gcd(R[0], R[i])
print('%d/%d' % (R[0] // g, R[i] // g))