BOJ 10473 - 인간 대포 링크
(2023.10.04 기준 G2)

문제

현재 위치한 좌표와 목적지의 좌표 그리고 대포 n개의 좌표가 주어진다.
걸어가는 속도는 5m/s이며, 대포를 타고 날아가면 원하는 임의의 방향으로 50m를 2초 동안 날아간다.
목적지까지 걸리는 최단 시간 출력

알고리즘

거리와 속도에 따라 걸리는 시간을 구해 다익스트라

풀이

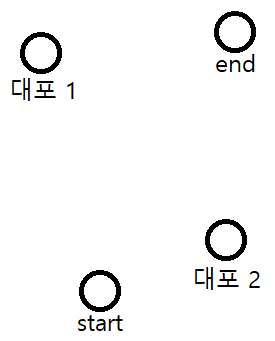
위와 같이 대포 2개가 주어졌다고 생각해보자.

우리가 구해야 하는 것은 거리 전부를 걸어가는 시간과 대포로 날아가고 남은 거리를 걸어가는 시간이다.
걸어가는 속도가 5m/s로 주어졌으므로 걸어가는 시간은 구하기 쉽다.

이제 대포를 이용해 가는 시간을 구해보자.

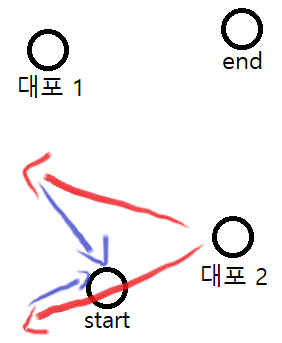
대포 2에서 start로 대포를 이용해 가려고 한다고 생각해보자.
어느 방향이든 대포로 날아갈 수 있다고 되어있지만, 목적지 방향으로 날아가서 남은 거리를 걸어가야 최단 거리로 갈 수 있다.

변 2개의 길이가 정해져 있는 삼각형을 생각해보자.
길이가 정해져 있는 두 변의 끼인 각이 커질수록 남은 변의 길이가 늘어나는 것은 자명하다.

가려고 하는 지점으로 날아가야 최단 거리가 됨을 알았으니, 이제 시간도 구해보자.

대포 2에서 각 지점으로 가려고 한다.
대포는 무조건 50m를 날아간다. 그러면 지점까지의 거리보다 덜 가든, 더 가든 상관없이 50m와의 차이만큼 더 걸어가야 한다.

위와 같이 각 지점 사이의 걸어가는 시간, 대포를 이용해 가는 시간을 구해 다익스트라를 돌려서 목적지로 가는 최단 거리를 구하면 된다. 물론, 대포를 이용해 가는 시간은 대포 지점에서 각 지점으로의 단방향 간선으로 그래프에 추가해야 한다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 102, inf = INT_MAX;

typedef pair<int, double> pid;
typedef pair<double, int> pdi;

struct point{
    double x, y;
};

point pos[MAXN];

double distance(point a, point b){
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    cin >> pos[0].x >> pos[0].y >> pos[1].x >> pos[1].y;
    int n; cin >> n; n += 2;
    for (int i = 2; i < n; i++) cin >> pos[i].x >> pos[i].y;

    vector<pid> graph[n];

    // v = m / s -> s = m / v
    // 걸어가거나 대포로 날아가서 나머지를 걸어가는 시간 구하기

    // 걸어가는 시간
    for (int i = 0; i < n - 1; i++) for (int j = i + 1; j < n; j++){
        double d = distance(pos[i], pos[j]) / 5;
        graph[i].push_back({j, d});
        graph[j].push_back({i, d});
    }

    // 대포로 날아가서 나머지를 걸어가는 시간
    for (int i = 2; i < n; i++) for (int j = 0; j < n; j++){ // 대포 위치에서 출발
        if (i == j) continue;

        // 대포로 날아가는 시간은 2초
        // 50m와의 차이만큼 걸어가야 한다.
        double d = 2 + fabs(50 - distance(pos[i], pos[j])) / 5;
        graph[i].push_back({j, d});
    }

    // 다익스트라
    priority_queue<pdi, vector<pdi>, greater<pdi>> pq; pq.push({0, 0});
    double dist[n]; dist[0] = 0; fill(dist + 1, dist + n, inf);
    while (!pq.empty()){
        auto [d, i] = pq.top(); pq.pop();
        if (dist[i] < d) continue;
        for (auto [j, dd]: graph[i]) if (dist[j] > d + dd){
            dist[j] = d + dd;
            pq.push({dist[j], j});
        }
    }

    cout << dist[1];
}

• Python

import sys; input = sys.stdin.readline
from math import inf
from heapq import heappop, heappush

def distance(a, b):
    return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5

pos = [tuple(map(float, input().split())) for _ in range(2)]

for _ in range(int(input())):
    pos.append(tuple(map(float, input().split())))

n = len(pos)
graph = [[] for _ in range(n)]

# v = m / s -> s = m / v
# 걸어가거나 대포로 날아가서 나머지를 걸어가는 시간 구하기

# 걸어가는 시간
for i in range(n - 1):
    for j in range(i + 1, n):
        d = distance(pos[i], pos[j]) / 5
        graph[i].append((j, d))
        graph[j].append((i, d))

# 대포로 날아가서 나머지를 걸어가는 시간
for i in range(2, n): # 대포 위치에서 출발
    for j in range(n):
        if i == j:
            continue

        # 대포로 날아가는 시간은 2초
        # 50m와의 차이만큼 걸어가야 한다.
        d = 2 + abs(50 - distance(pos[i], pos[j])) / 5
        graph[i].append((j, d))

# 다익스트라
pq = [(0, 0)]
dist = [inf] * n
dist[0] = 0
while pq:
    d, i = heappop(pq)
    if dist[i] < d:
        continue
    for j, dd in graph[i]:
        if dist[j] > d + dd:
            dist[j] = d + dd
            heappush(pq, (dist[j], j))

print(dist[1])