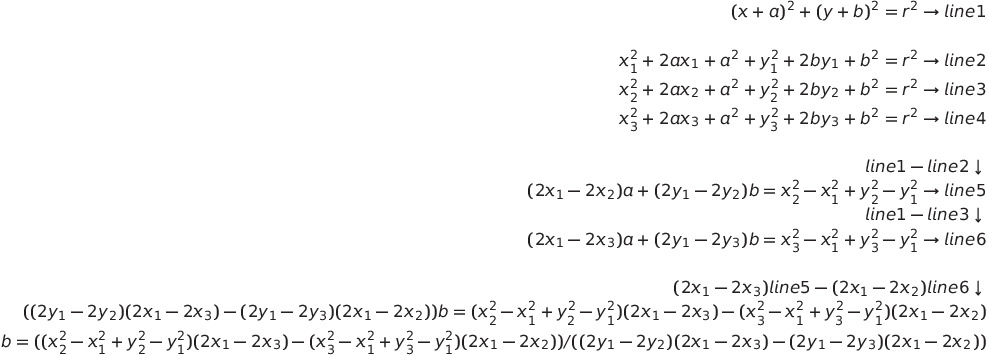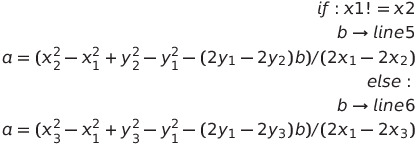불금이다 무야호

BOJ 6600 - 원의 둘레 링크
(2022.11.04 기준 S3)
(치팅 나빠요)

문제

일직선 상에 있지 않은 세 점이 주어질 때, 이 세 점을 이용하여 만들 수 있는 원의 원주 출력

알고리즘

원의 방정식과 세 점을 이용하여 방정식을 완성하고, 그 방정식을 통해서 반지름을 구한 다음에 원주를 구하면 된다. (그냥 수학 문제..)

풀이

학창시절, 원의 방정식을 모두 접해봤을 것이다.
(x + a) ** 2 + (x + b) ** 2 = r ** 2
여기서 a와 b를 구해야 한다.
a와 b를 변수로 두고 x와 y에 세 점의 좌표를 대입하면 세 식이 나오고, r ** 2를 지워나가면 연립방정식이 나온다.
이를 정리하여 a와 b를 구하고 세 점 중 하나를 대입하여 r을 구한 다음에 원주를 구하면 끝!

참 간단한.. 수학 문제다...

b를 먼저 구하는 과정
a를 구하는 과정
x1과 x2가 같으면 0으로 나누게 되는 것이므로 주의해야 한다.

코드

import sys; input = sys.stdin.readline
from math import pi

while True:
    try: # EOF 처리
        x1, y1, x2, y2, x3, y3 = map(float, input().split())
    except:
        break

    # 풀이에서 식 정리를 보자.
    # 필요한 제곱들
    x12 = x1 ** 2
    x22 = x2 ** 2
    x32 = x3 ** 2
    y12 = y1 ** 2
    y22 = y2 ** 2
    y32 = y3 ** 2

    # b, a, r을 순서대로 구하자
    b = ((x22 - x12 + y22 - y12) * (2 * x1 - 2 * x3) - (x32 - x12 + y32 - y12) * (2 * x1 - 2 * x2)) / ((2 * y1 - 2 * y2) * (2 * x1 - 2 * x3) - (2 * y1 - 2 * y3) * (2 * x1 - 2 * x2))
    try:
        a = (x22 - x12 + y22 - y12 - (2 * y1 - 2 * y2) * b) / (2 * x1 - 2 * x2)
    except:
        a = (x32 - x12 + y32 - y12 - (2 * y1 - 2 * y3) * b) / (2 * x1 - 2 * x3)
    r = ((x1 + a) ** 2 + (y1 + b) ** 2) ** 0.5

    # 원의 둘레는 2 * pi * r
    print(format(2 * pi * r, '.2f'))

여담

공책에 적어가면서 풀었더니
오랜만에 학생이 된 느낌. 껄껄껄