회전하는 캘리퍼스 문제 중 먼 별(13310)이라는 문제가 있다.
풀려고 했지만 삼분 탐색을 이용해야 하는 문제라, 결국 삼분 탐색을 공부했다.

삼분 탐색을 공부한 기념으로 가장 베이직한 삼분 탐색 문제를 풀이해보겠다.

BOJ 8986 - 전봇대 링크
(2022.10.24 기준 P5)
(치팅하면 길가다가 전봇대에 부딪힘)

문제

전봇대의 수 N과 서로 다른 전봇대의 위치 xi가 N개만큼 오름차순으로 주어질 때
모든 이웃한 전봇대들의 거리가 같도록 하는 전봇대들의 이동거리의 합의 최솟값 출력. 단, x0 = 0이다.

알고리즘

전봇대들의 거리 x에 따른 이동거리 합 y는 아래가 볼록한 함수 꼴이다. 이 함수의 극값을 찾기 위해 삼분 탐색을 해야 한다. 자세한 내용은 풀이에서 후술.

풀이

문제 예제 1번을 살펴보자.

만약 거리를 0으로 잡고 전봇대를 이동한다면 (N이 1이 아니면 절대 답이 될 리는 없지만)
모든 전봇대의 위치가 0이 되어야 한다면 0 + 4 + 6 + 9 = 19

만약 거리를 1로 잡고 전봇대를 이동한다면
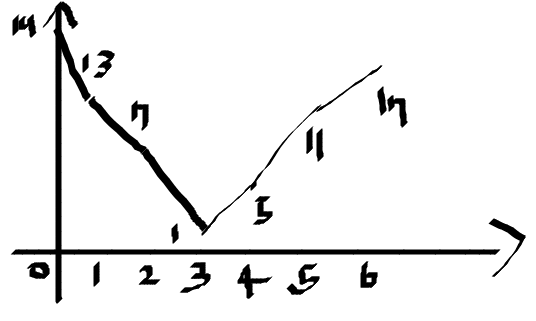
전봇대들의 위치는 [0, 1, 2, 3]이 되어야 하므로 0 + 3 + 4 + 6 = 13

이를 반복하여 거리 6까지만 이동거리의 합을 구해서 그래프를 나타내보면

이렇게 아래가 볼록한 그래프 모양이 나타난다.
이 예제의 답은 거리 3에 따른 1이 된다.

결국 이 문제는 아래가 볼록한 그래프의 극솟갑을 찾아야 하는 문제다.
위나 아래가 볼록한 그래프의 극값은 삼분 탐색으로 찾아야 한다.

삼분 탐색은 이분 탐색과 큰 틀은 비슷하다.
범위의 양 끝을 정하고 중간값에 따라 범위를 좁혀나가는 것인데
다만, 삼분 탐색은 중간값 2개를 잡고 그 함수 결과에 따라 범위를 좁혀나가야 한다.
이 문제는 아래가 볼록하므로 극솟값을 찾아야 한다. 그러므로 함수 결과가 더 작은 중간값을 중심으로 범위를 좁혀나가야 한다. 왜냐면, 극솟값을 찾아야 하므로 함수 결과가 더 높은 쪽은 극솟값이 없는 범위이니깐.

삼분 탐색 코드는 간단하다.
주석을 보면서 코드를 보면 바로 이해가 갈 것이니 참고하자.

코드

import sys; input = sys.stdin.readline
from math import inf

def f(x): # 함수
    result = 0
    for i in range(N):
        result += abs(X[i] - x * i)
    return result

N = int(input())
X = list(map(int, input().split()))

# ternary search
start = 1; end = 1000000000
while end - start >= 3: # 차이가 3 이상인 동안만
    mid_1 = (start * 2 + end) // 3 # 왼쪽 중간값
    mid_2 = (start + end * 2) // 3 # 오른쪽 중간값
    # 아래가 볼록한 함수이므로 극솟값을 찾아야 한다.
    # 함수값이 더 큰 쪽은 극솟값을 가질 수 없는 범위
    if f(mid_1) < f(mid_2):
        end = mid_2
    else:
        start = mid_1

# 찾아낸 [start, end] 구간에서 극솟값을 찾자.
result = inf
for x in range(start, end + 1):
    result = min(result, f(x))

print(result)

여담

삼분 탐색 자체는 정말 간단한 것 같다. 하지만, 문제들이 대놓고 어떻게 구해라하고 그렇지는 않고, 어렵게 함수와 그래프 모양을 찾아내야 하는 문제들이 대부분인 것 같다.
쉽지 않아