결국 삼분 탐색을 공부하고 이 문제를 풀게 되었다. 뿌듯하다. 그래서 풀이를 적어보겠다.

BOJ 13310 - 먼 별 링크
(2022.10.24 기준 D5)
(치팅하면 진짜.. 걸릴걸..?)

문제

N개의 별이 있고 각 별은 좌표 (x, y)와 속도 [dx, dy]를 가지고 있다.
0일부터 T일까지 별을 촬영했을 때, 가장 멀리 떨어진 두 별의 거리가 최소인 촬영일과 그 때 거리의 제곱값 출력

알고리즘

가장 멀리 떨어진 두 별의 거리는 회전하는 캘리퍼스
촬영일마다 회전하는 캘리퍼스의 결과값을 그래프로 나타내면 아래가 볼록한 모양. 그러므로 삼분 탐색

풀이

별은 한 방향으로 일정한 속도로 쭉 간다.
그럼 어떤 두 별이라도 가까워지다가 영원히 멀어져 간다. 물론, 가까워지지 않는 경우도 있다. 두 별이 처음부터 멀어질수도 있다. 그리고 같은 방향으로 같은 속도로 간다면 두 별의 거리는 영원히 일정할 것이다. 하지만 절대 두 별이 영원히 가까워지는 경우는 없다.
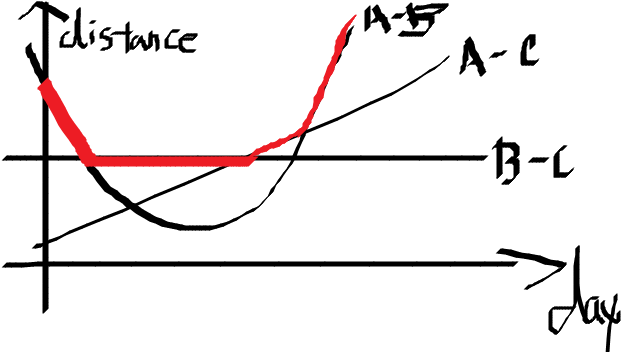
결국은 두 별의 거리의 그래프의 모양은 ∪, -, / 모양 중 하나가 나온다.

A, B, C 세 별이 있고 A와 B의 거리는 ∪ 모양, A와 C의 거리는 / 모양, B와 C의 거리는 - 모양이라고 가정해보자. 이를 그래프로 나타내면

이렇게 나타나지는데, 촬영일마다 가장 멀리 떨어진 두 별의 거리를 구해야 하므로 빨간 부분을 구해야 하는 것이다. 이 빨간 부분은 아래가 볼록한 모양이므로 결국 촬영일을 범위로 잡아 삼분 탐색을 해서 구해야 한다.

빨간 부분은 어떻게 구하냐.
별이 한 점이라고 생각하고 많은 별이 있다고 생각해보자. 그 많은 별 중 가장 멀리 떨어진 두 별은 볼록 껍질의 최대 직경이 되는 것이다. 결국, 회전하는 캘리퍼스의 결과가 촬영일에 따른 함수 값이 되는 것이다.

보기엔 복잡해보이지만, 삼분 탐색과 회전하는 캘리퍼스를 기본적으로 아는 상태이면 쉽게 풀 수 있는 문제이다.

코드

import sys; input = sys.stdin.readline
from math import inf

def ccw(a, b, c): # a-b-c가 반시계 방향인지 검사
    if (a[0] * b[1] + b[0] * c[1] + c[0] * a[1]) - (a[1] * b[0] + b[1] * c[0] + c[1] * a[0]) > 0:
        return True
    return False

def dist(a, b): # a-b 거리 계산 (제곱 형태로 반환)
    return (a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2

def f(t): # 함수 (별들의 볼록 껍질의 최대 직경. 즉, 회전하는 캘리퍼스)
    points = [] # 별들의 좌표
    for x, y, dx, dy in stars:
        points.append((x + dx * t, y + dy * t)) # 촬영일과 속도에 따른 좌표를 구해준다.

    # monotone chain
    # x, y가 오름차순이 되게 정렬
    points.sort()

    # 볼록 껍질의 아래
    down = []
    for i in range(N):
        while len(down) > 1:
            if ccw(down[-2], down[-1], points[i]):
                break
            down.pop()
        down.append(points[i])

    # 볼록 껍질의 위
    up = []
    for i in range(N - 1, -1, -1):
        while len(up) > 1:
            if ccw(up[-2], up[-1], points[i]):
                break
            up.pop()
        up.append(points[i])

    # 위와 아래를 합쳐 볼록 껍질을 만들고
    # 볼록 껍질의 꼭짓점 개수와 회전하는 캘리퍼스의 두 시작점과 두 시작점의 거리를 구하자.
    hull = down[:-1] + up[:-1]
    size = len(hull)
    lp = 0; rp = len(down) - 1
    result = dist(hull[lp], hull[rp])
    # 회전하는 캘리퍼스
    # 반시계 방향으로 돌려가면서 직경을 구해나감
    for _ in range(size):
        lx, ly = hull[lp]
        llx, lly = hull[(lp + 1) % size]
        rx, ry = hull[rp]
        rrx, rry = hull[(rp + 1) % size]
        # 직경이 작아지지 않게끔 다음 점을 구함
        if ccw([llx - lx, lly - ly], [0, 0], [rrx - rx, rry - ry]):
            lp = (lp + 1) % size
        else:
            rp = (rp + 1) % size
        result = max(result, dist(hull[lp], hull[rp]))
    return result

N, T = map(int, input().split())
stars = [list(map(int, input().split())) for _ in range(N)]
start = 0; end = T # 촬영일의 범위
while end - start >= 3: # 차이가 3 이상인 동안만
    mid_1 = (start * 2 + end) // 3
    mid_2 = (start + end * 2) // 3
    if f(mid_1) <= f(mid_2): # 함수값에 따라 범위를 좁혀나간다.
        end = mid_2
    else:
        start = mid_1

# 찾아낸 [start, end] 구간에서 극솟값을 찾자.
answer = [0, inf]
for day in range(start, end + 1):
    result = f(day)
    if result < answer[1]:
        answer = [day, result]
print(*answer, sep = '\n')

여담

첫 다이아 문제 풀이였다. 나는 6번째 다이아 문제 AC.

점점 다이아 문제로 채워지는 느낌이 들어서 좋다. (그래봤자 아직 6개지만..)