BOJ 12909 - 그래프 만들기 링크
(2024.03.18 기준 G1)

문제

트리의 점수는 각 노드의 점수를 더해서 구할 수 있고, 각 노드의 점수는 차수에 따라 정해진다.
트리의 정점의 개수 $N$과 차수에 따른 점수가 주어질 때, 가능한 점수의 최댓값 출력

알고리즘

Top-Down DP

풀이

현재 사용 가능한 정점의 개수를 $n$, 현재 보고 있는 트리의 루트의 차수를 $d$라고 하자.

이제 현재 보고 있는 루트에 자식 노드를 달아보자. 이때 자식 노드를 루트로 한 서브트리의 크기를 정해야 한다. 서브트리의 크기는 $1$ 이상 $n-1$ 이하가 될 수 있다. 현재 보고 있는 트리의 루트로 쓸 수 있는 정점 하나는 남겨놓아야 하기 때문이다.
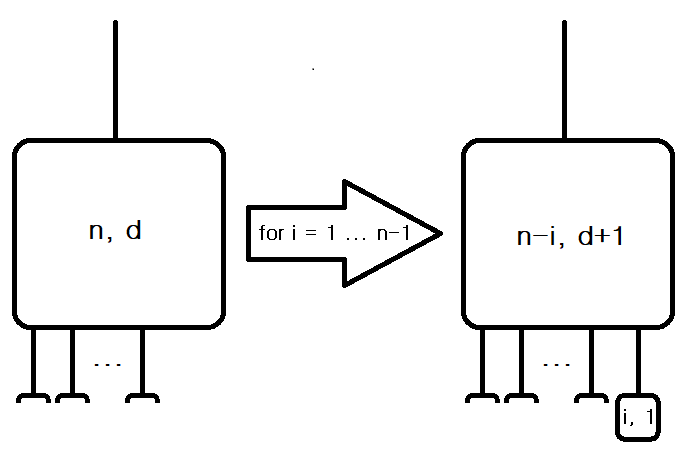
이렇게 서브트리의 크기 $i$를 정해서 자식 노드를 달아주면, 현재 사용 가능한 정점의 개수는 $n-i$, 현재 보고 있는 트리의 루트의 차수는 $d+1$이 된다.

위 과정을 점화식으로 세워보면 $dp(n,d) = \max_{i=1}^{n-1} (dp(i, 1)+dp(n-i,d+1))$가 된다. 그림으로 표현해보면 아래와 같이 표현할 수 있다.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 52;

int N, V[MAXN], dp[MAXN][MAXN];

int dfs(int n, int d){
    if (n == 1) return V[d];
    if (~dp[n][d]) return dp[n][d];
    dp[n][d] = 0;
    for (int i = 1; i < n; i++) // 자식 노드를 추가한다. 자식 노드를 루트로 한 서브트리의 크기는 i
        // 서브트리의 차수는 일단 1로 시작, 현재 트리의 차수는 1 증가하며 사용 가능한 정점은 i개 감소
        dp[n][d] = max(dp[n][d], dfs(i, 1) + dfs(n - i, d + 1));
    return dp[n][d];
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    cin >> N;
    V[0] = 0; for (int i = 1; i < N; i++) cin >> V[i];
    fill(&dp[0][0], &dp[N][N + 1], -1);
    cout << dfs(N, 0);
}

• Python

import sys; input = sys.stdin.readline

def dfs(n, d): # 남은 정점 수, 현재 차수
    if n == 1:
        return V[d]
    if ~dp[n][d]:
        return dp[n][d]
    dp[n][d] = 0
    for i in range(1, n): # 자식 노드를 추가한다. 자식 노드를 루트로 한 서브트리의 크기는 i
        # 서브트리의 차수는 일단 1로 시작, 현재 트리의 차수는 1 증가하며 사용 가능한 정점은 i개 감소
        dp[n][d] = max(dp[n][d], dfs(i, 1) + dfs(n - i, d + 1))
    return dp[n][d]

N = int(input())
V = [0] + list(map(int, input().split()))

dp = [[-1] * (N + 1) for _ in range(N + 1)]
print(dfs(N, 0))