BOJ 15910 - 바나나나빠나나 링크
(2024.05.09 기준 G1)

문제

유사 바나나는 다음과 같이 정의된다.

• BANANA는 유사 바나나이다.
• 유사 바나나 앞에 B를 붙인 것 또한 유사 바나나이다. 예를 들어, BBANANA는 유사 바나나이다.
• 유사 바나나 뒤에 NA를 붙인 것 또한 유사 바나나이다. 예를 들어, BANANANA나 BBANANANA는 유사 바나나이다.

유사 바나나 문자열은 하나 이상의 유사 바나나를 나열한 것이다.

B, A, N으로 이루어진 문자열이 주어질 때, 유사 바나나 문자열로 만들기 위해서 문자를 바꾸는 횟수의 최솟값 출력

알고리즘

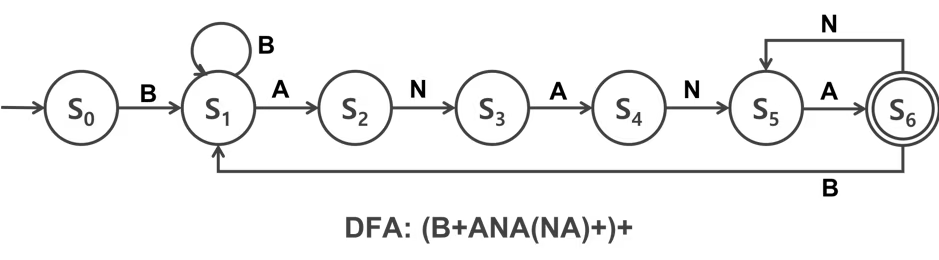
문제 힌트에 나와 있는 DFA 그림을 이용한 dp

풀이

문제 힌트에 나와 있는 DFA 그림을 그대로 2차원 dp로 나타내면 된다.

$dp(i, j)$를 문자열 $T$의 $i$번째 문자가 $S_j$일 때의 최적값이라고 정의하자.
상태는 $S_0$, $S_1$, $\dots$, $S_7$로 총 $7$개가 있다. 각 간선을 이용해서 dp를 채워주면 된다.
예를 들어, $S_1$은 $S_0$, $S_1$, $S_6$에서 넘어올 수 있음을 알 수 있다. 이를 식으로 나타내면 다음과 같다.
$dp(i, 1) = min(dp(i - 1, 0), dp(i - 1, 1), dp(i - 1, 6)) + (0 \text{ if }T_i = \text{B else } 1)$

코드

• C++

#include <bits/stdc++.h>
using namespace std;

const int inf = 1e8;

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    string S; cin >> S;
    int M = S.size();

    // DFA를 dp로 나타낸다.
    int dp[M + 1][7]; fill(&dp[0][0], &dp[M][7], inf);
    dp[0][0] = 0;

    for (int i = 1; i <= M; i++){

        // S1 : S0 -> S1, S1 -> S1, S6 -> S1
        dp[i][1] = min({dp[i - 1][0] + (S[i - 1] != 'B'), dp[i - 1][1] + (S[i - 1] != 'B'), dp[i - 1][6] + (S[i - 1] != 'B')});

        // S2 : S1 -> S2
        dp[i][2] = dp[i - 1][1] + (S[i - 1] != 'A');

        // S3 : S2 -> S3
        dp[i][3] = dp[i - 1][2] + (S[i - 1] != 'N');

        // S4 : S3 -> S4
        dp[i][4] = dp[i - 1][3] + (S[i - 1] != 'A');

        // S5 : S4 -> S5, S6 -> S5
        dp[i][5] = min(dp[i - 1][4] + (S[i - 1] != 'N'), dp[i - 1][6] + (S[i - 1] != 'N'));

        // S6 : S5 -> S6
        dp[i][6] = dp[i - 1][5] + (S[i - 1] != 'A');
    }

    cout << dp[M][6];
}

• Python

import sys; input = sys.stdin.readline
from math import inf

S = input().strip()
M = len(S)

# DFA를 dp로 나타낸다.
dp = [[inf] * 7 for _ in range(M + 1)]
dp[0][0] = 0

for i in range(1, M + 1):

    # S1 : S0 -> S1, S1 -> S1, S6 -> S1
    dp[i][1] = min(dp[i - 1][0] + (S[i - 1] != 'B'), dp[i - 1][1] + (S[i - 1] != 'B'), dp[i - 1][6] + (S[i - 1] != 'B'))

    # S2 : S1 -> S2
    dp[i][2] = dp[i - 1][1] + (S[i - 1] != 'A')

    # S3 : S2 -> S3
    dp[i][3] = dp[i - 1][2] + (S[i - 1] != 'N')

    # S4 : S3 -> S4
    dp[i][4] = dp[i - 1][3] + (S[i - 1] != 'A')

    # S5 : S4 -> S5, S6 -> S5
    dp[i][5] = min(dp[i - 1][4] + (S[i - 1] != 'N'), dp[i - 1][6] + (S[i - 1] != 'N'))

    # S6 : S5 -> S6
    dp[i][6] = dp[i - 1][5] + (S[i - 1] != 'A')

print(dp[M][6])