난 요즘 메이플스토리를 한다. 아주 꿀잼임.
그래서 메이플에 관한 문제를 들고 왔다!
BOJ 20925 - 메이플스토리 링크
(2022.10.21 기준 G2)
(치팅하면 평생 스틸당함. 자리요)
문제
사냥터 N개와 시간 T분이 있고, 사냥터 입장에 필요한 최소 경험치 c와 1분마다 얻는 경험치 e가 각 사냥터마다 정해져 있을 때, 총 얻을 수 있는 경험치의 최댓값 출력. 단, c가 0인 사냥터는 반드시 하나 이상 존재한다.
알고리즘
전형적인 Bottom-Up DP
c가 0인 사냥터에서 1분 단위로 사냥을 해나가자.
풀이
사냥터 수는 최대 200개, 시간 단위는 최대 1000분, 1분마다 경험치가 얻어지고 사냥터를 옮길지 정하기 때문에
dp는 사냥터 수 N * 분 단위 T 행렬로 만들고 dp 값은 얻을 수 있는 최대 경험치로 채워가면 된다.dp는 점화식이 중요하다.
t분일 때 i번 사냥터에서 얻을 수 있는 경험치는 두 개의 경우가 있다.
- t-1분일 때 i번 사냥터에서 계속 사냥을 한 경우
이는 t-1분일 때 i번 사냥터에 있을 수 있느냐가 중요한 포인트이다. 이는 dp를 -1로 초기화하고 갈 수 있는 사냥터는 0 이상이 되게 한 다음에 dp[t-1][i] > -1 조건을 걸면 된다.
- j번 사냥터에서 옮겨 온 경우이다.
이 부분이 중요하다. 옮겨 올 때 체크해야 하는 부분은 두 가지다.
첫번째는 j번 사냥터에서 i번 사냥터로 이동하는 시간이 현재 시간보다 같거나 작아야 한다.
음수인 시간대에서 넘어올 수 없기 때문.
두번째는 dp[t - move[j][i]][j]는 j번 사냥터에서 넘어올 때 경험치인데 이 경험치가 i번 사냥터 입장에 필요한 최소 경험치를 넘어야 한다.
두 조건을 식으로 나타내면 t - move[j][i] >= 0 && dp[t - move[j][i][j] >= C[i] 가 된다.이 두 개의 경우를 토대로 점화식을 세워보면
dp[t][i] = max(dp[t - 1][i] + E[i] (dp[t - 1][i] > -1), dp[t - move[j][i]][j] (t - move[j][i] >= 0 and dp[t - move[j][i]][j] >= C[i]))여기서 의아한 점이 있을 것인데 왜 dp[t - move[j][i] - 1][j] + E[i]가 아닐까?
넘어오는데 걸리는 시간에 사냥까지 하면 되는데 말이다. 하지만 이는 심각한 오류를 범하는 것이다.
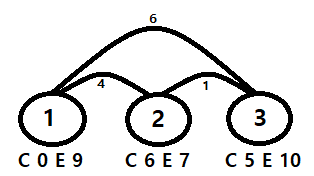
아래의 그림을 보자.
1번 사냥터에서 사냥을 시작하면 2번과 3번으로 넘어갈 수 있다.
3번으로 바로 넘어가면 6초가 걸리지만 1-2-3번 루트를 타면 5초가 걸린다.
근데 여기서 만약 dp[t - move[j][i] - 1][j] + E[i]를 써버린다면?
1번에서 2번으로 옮긴 다음 무조건 1분 사냥을 하고 3번으로 옮겨 버리게 되는 것이다.
당연히 1번에서 2번, 2번에서 3번으로 바로 옮기는 것이 최대 경험치를 얻게 될 것이다.
그래서 사냥터를 옮기는 경우에는 옮기는 경우만 생각하는 것이다.
코드
import sys; input = sys.stdin.readline
N, T = map(int, input().split())
C = [] # 입장하기 위한 최소 경험치
E = [] # 1분마다 얻는 경험치
for _ in range(N):
c, e = map(int, input().split())
C.append(c)
E.append(e)
move = [list(map(int, input().split())) for _ in range(N)] # i -> j 이동 시간을 나타내는 인접 행렬
# dp[t][i] = max(dp[t - 1][i] + E[i], dp[t - move[j][i]][j])
# dp[t - 1][i] + E[i]는 t - 1분에 i번 사냥터에서 사냥을 했어야 가능
# dp[t - move[j][i]][j]는 (t - move[j][i] >= 0 and dp[t - move[j][i]][j] >= C[i])를 만족해야 함.
# 위 두 조건으로 dp를 채워나가자.
dp = [[-1] * N for _ in range(T + 1)]
# 입장하기 위한 최소 경험치가 0인 사냥터를 시작 사냥터로 골라야 하므로
# C[i] = 0 이면 dp[0][i] = 0 으로 만들자.
for i in range(N):
if not C[i]:
dp[0][i] = 0
for t in range(1, T + 1):
for i in range(N):
if dp[t - 1][i] > -1: # 같은 사냥터에서 계속 사냥하는 경우
dp[t][i] = dp[t - 1][i] + E[i]
for j in range(N): # j번 사냥터에서 i번 사냥터로 넘어오는 경우 (넘어온 상태만 입력)
if i != j and t - move[j][i] >= 0 and dp[t - move[j][i]][j] >= C[i]:
dp[t][i] = max(dp[t][i], dp[t - move[j][i]][j])
print(max(dp[-1]))여담
실수하기 쉬운 DP 문제였다.
생각보다 어려웠음.
아 얼른 집가서 메이플 하고싶다