Codeforces Round #812 (Div. 2) - Optimal Reduction 링크
(2022.08.29 기준 Difficulty *1000)

문제

한 배열이 있을 때, 어떤 범위를 정하여 그 범위에 있는 원소를 1씩 감소시키는 연산을 반복하여 모든 원소를 0으로 만들 때 최소 연산 수를 f(a)라고 하자.
a의 모든 순열 b에 대해 f(a) ≤ f(b)가 참인지 출력

알고리즘

배열의 정렬 상태를 보고 판단해야 하는 문제

풀이

연산을 직접 차근차근 해보면 알아낼 수 있는 특징이 있다.

연산은 감소만 있고 증가는 없다.
그러므로 범위 안 원소에 0이 있으면 (증가 연산이 없으므로) 안된다.
만약 0이 있다면 0을 기준으로 범위가 앞뒤 두 부분으로 나뉘어져서 최소 연산 수가 늘어난다.
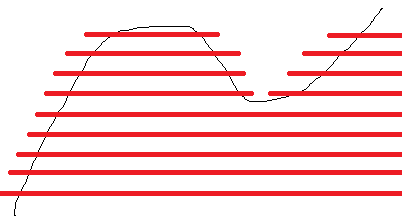
그림으로 쉽게 표현해보자면

만약 이런 산을 밑에서부터 한 칸씩 깎아내려 간다고 생각하면
중간에 범위가 끊겨버려 두 번씩 깎아내려야 한다.
이 연산도 똑같이 생각하면 된다.
원소의 수가 높이인 히스토그램이라고 생각했을 때, 중간에 움푹 파이는 곳이 생기면 안된다.

즉, a의 원소가 감소하다가 증가할 경우, f(a) ≤ f(b)가 성립되지 않는다.
(a가 오름차순이나 내림차순으로 정렬된 b의 연산 수 f(b)가 더 작아지기 때문)

코드

import sys; input = sys.stdin.readline

for _ in range(int(input())):
    n = int(input())
    a = list(map(int, input().split()))
    fall = False # 감소하고 있었음을 나타냄
    for i in range(n - 1):
        if a[i] > a[i + 1]:
            fall = True # 감소하고 있으면 fall 활성화
        elif a[i] < a[i + 1] and fall: # 만약 증가하는데 전에는 감소하고 있었으면
            print('NO') # a가 정렬된 순열인 b의 연산 f(b)가 f(a)보다 더 작다.
            break
    else:
        print('YES')

여담

이 문제는 말이 정렬이지. 약간, 애드혹 느낌이 난다.
역시 코드포스 문제는 창의적인 문제가 많아