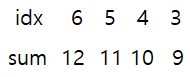Codeforces Round #812 (Div. 2) - Build Permutation 링크
(2022.08.29 기준 Difficulty *1200)

문제

원소 ai + i (0 ≤ i ≤ n-1) 가 제곱수가 되는 [0, 1, 2, …, n-1]의 순열 p 찾기

알고리즘

어떤 한 정수 x가 있으면 x와 2x 사이에 제곱수가 무조건 있다. 증명은 tutorial 보면 있음.
증명 링크
그러므로 ai + i가 될 수 있는 제곱수 중 가장 큰 제곱수를 구하려면 마지막 인덱스인 n-1에 대해서 제곱수를 구하면 된다. [n-1, 2(n-1)] 사이에 있을 것인데 sqrt(2*(n-1))의 제곱이다. 증명은 생략.

이를 재귀적으로 풀어내야 한다.

풀이

알고리즘에서 설명했듯이 n - 1에 대해서 제곱수를 먼저 구하자.
제곱수를 구하면 n - 1부터 감소시키면서 n - 1을 더하면 제곱수가 되는 인덱스를 찾아야 한다. 그 인덱스를 j라고 하면 인덱스 j부터 n - 1까지에다가 n - 1부터 j까지를 더하면 그 범위 안 모든 원소 ai에 대해 ai + i는 제곱수가 될 것이다.

만약 n이 7이라고 생각해보자.
sqrt(2*(n-1))의 제곱은 9다. 그러면 n - 1부터 감소시키면서 n - 1을 더하면 9가 되는 인덱스를 찾아보자.

j는 3이다.
그러면 3부터 6까지에다가 6부터 3까지를 더하면
[?, ?, ?, 6 + 3 = 9, 5 + 4 = 9, 4 + 5 = 9, 3 + 6 = 9] 가 된다.
그러므로 구하고자 하는 배열 p의 인덱스 3~6은 [6, 5, 4, 3]이 된다.

이렇게 인덱스 j부터의 배열 p를 구했으니 남은 것은 0 ~ j-1
이는 또 위에서 구한 것처럼 똑같이 구해주면 된다. (재귀)

코드

import sys; input = sys.stdin.readline

def solve(n):
    if n < 0:
        return
    square = int((2 * n) ** 0.5) ** 2 # 제곱수를 구한다.
    for i in range(n, -1, -1):
        if i + n == square: # 더하면 제곱수가 되는 인덱스를 구했으면
            for j, k in zip(range(i, n + 1), range(n, i - 1, -1)):
                answer[j] = k # 출력할 배열에 차례대로 값을 넣어준다.
            break
    solve(i - 1) # 남은 인덱스도 구해준다.

for _ in range(int(input())):
    n = int(input())
    answer = [0] * n
    solve(n - 1)
    print(*answer)

여담

Codeforces Round #812 D번 문제는 내가 처음 보는 유형의 문제라서 멘붕이 왔다.
그 뒤에 E, F번 문제는 아직 공부하지 않은 알고리즘 문제인 것 같았다.
그래서 C번까지만 풀이를 적어볼까 한다.

물론, 나중에 실력이 더 향상되면 다 풀어서 풀이 적을 것이다!
그전까지 기다려랏!!