옛날 백준보다도 먼저 접했었던 프로그래머스.
오랜만에 들어갔는데 많이 바뀌었다.
들어간 기념으로 아무거나 한 문제 잡고 풀었는데 흐미.. 되게 쉽다.
일단 풀이를 적어보겠다.

프로그래머스 - 도둑질 링크
(2022.08.16 기준 Level 4)
(Don't Cheat!)

문제

인접하지 않게 최대한 많이 고를 수 있는 최댓값

알고리즘

그냥 DP
DP의 정석.

풀이

흔히 볼 수 있는 DP 문제 유형이다.
백준의 스티커, 계단 오르기. 더 나아가서 습격자 초라기와 비슷하다.
먼저 인접한 두 집을 털면 경보장치가 울린다. 이를 토대로 최대한 많은 액수를 털어야 하는데 점화식을 바로 떠올릴 수 있다.
money를 각 집을 털면 얻을 수 있는 액수라 하면

dp[i] = max(dp[i - 1], dp[i - 2] + money[i])

i까지의 결과는 max(i-1까지의 결과, i-2까지의 결과 + i번째 집 액수) 이다.
i-2까지 턴 것에 i번째 집 액수를 합쳐도 i-1까지 털었을 때가 더 많을 수 있기 때문이다.

근데 여기서 중요한 것은

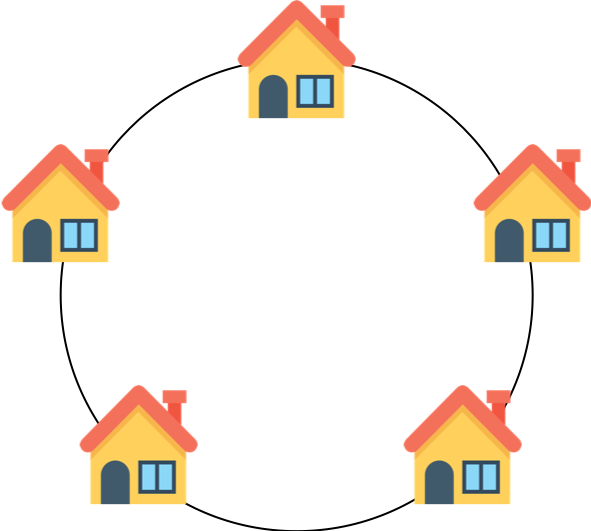
모든 집들은 동그랗게 배치되어 있어서 첫번째와 마지막 집도 연결되어 있다...!
그러므로 dp를 2차원으로 선언하자.
dp 첫번째 열은 첫번째와 마지막 집이 연결되어 있지 않은 일반적인 점화식으로
그리고 두번째 열에는 첫번째를 털었다고 가정했을 때, 마지막 전 집까지의 점화식으로.
dp를 채우고 나면, dp[-1][0]과 dp[-2][1]을 비교하여 큰 값으로 출력(반환)하면 된다.

코드

def solution(money):
    money = [0] + money # dp를 채우기 위해 맨 앞에 0 원소를 추가한다.
    m = len(money)
    dp = [[0] * 2 for _ in range(m)]
    dp[1][1] = money[1] # 첫번째 집을 털었다고 가정
    for i in range(2, m - 1): # dp 두 열 모두 마지막 전까지 진행
        dp[i][0] = max(dp[i - 1][0], dp[i - 2][0] + money[i])
        dp[i][1] = max(dp[i - 1][1], dp[i - 2][1] + money[i])
    dp[-1][0] = max(dp[-2][0], dp[-3][0] + money[-1]) # dp 첫 열은 마지막까지 진행
    return max(dp[-1][0], dp[-2][1])

여담

예전에는 프로그래머스 Level 3도 벅찼다는 느낌을 받았는데
많이 공부하고 와서 그런지 Level 4도 정말 쉽더라. 이 문제가 Level 4 문제 중에서 쉬운 편인걸까?
백준으로 따지면 S1~G4 정도 되는 것 같다.

뭐 아무튼 내 실력이 늘어난 게 확실히 보여서 기분이 좋다.