4/15 분할 정복(Divide & Conquer)

분할 정복 (Divide & Conquer)
분할 정복은 문제를 여러개로 나누어서 푸는 알고리즘입니다.

기존 문제를 바로 풀 수 없다면 Divde로 문제를 나누면 되는데 Divide로 나눈 후 나눈 부분 문제가 Base Case인지 Recursive Case인지 구분하면 됩니다.
Base Case는 이미 문제가 충분히 작아서, 더 작은 부분 문제로 나누지 않아도 바로 답을 구할 수 있는 경우를 의미합니다.
Recusrive Case는 문제가 커서 바로 답을 알 수 없어서, 같은 형태의 부분 문제들로 쪼개야 하는 경우를 의미합니다.
문제를 Base Case가 나올 때까지 Divide한 다음에 답을 구한(Conquer) 후 부분 문제들의 결합(Combine)으로 기존 문제를 해결해 나가면 됩니다.

동적 계획법(DP)과의 차이점은
동적 계획법은 분할한 문제들이 서로 영향을 미침.
분할 정복은 분할한 문제들이 서로 영향을 미치지 않음.
이 있습니다.

분할 정복의 필요조건

1. 문제를 나눌 수 있어야 합니다.
2. 부분 문제의 답을 이용하여 원래 문제의 답을 계산하는 방법이 있어야 합니다.

분할 정복의 알고리즘의 접근법은 다음과 같습니다.

분할 : 문제를 작은 문제로 분할하는 과정
정복 : 분할한 작은 문제들을 해결.
조합 : 작은 문제에 대한 결과를 원본 문제에 대한 결과로 조합합니다

퀵정렬(Quick Sort)
대표적인 분할정복 알고리즘입니다.
내부정렬 : 추가 리스트를 사용하지 않음 (합병정렬과 반대)

[Divide] : 기준 원소(pivot)를 정해서 좌우 분할
[Conquer] : 왼쪽과 오른쪽 리스트를 각각 재귀적으로 퀵정렬
[Obtain] : 정렬된 리스트 리턴

💡 기준원소(pivot)는 어떻게 정하나?
편의상 리스트의 첫 원소를 기준원소로 정하자

💡 기준원소로 어떻게 나눌수 있는가?
두개의 인덱스(i,j)로 비교, 교환

분할 정복을 이용한 알고리즘 문제를 풀어보았습니다.

문제 링크

색종이 만들기 성공

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 128 MB 34397 23675 18458 69.043%

문제
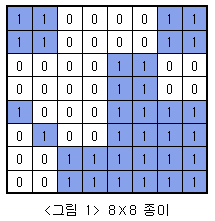
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.

전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.
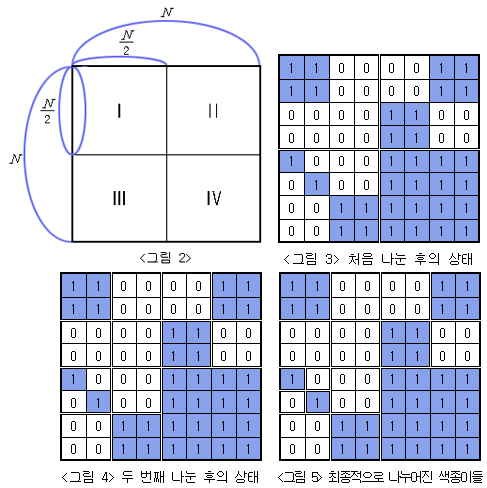
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.

입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.

입력
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.

출력
첫째 줄에는 잘라진 햐얀색 색종이의 개수를 출력하고, 둘째 줄에는 파란색 색종이의 개수를 출력한다.

예제 입력 1
8
1 1 0 0 0 0 1 1
1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
1 0 0 0 1 1 1 1
0 1 0 0 1 1 1 1
0 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1

예제 출력 1
9
7

import sys

n = int(input()) #테이블 테스트 개수
lst = [] #주어진 8개의 리스트
for _ in range(n):
    lst.append(list(map(int, input().split())))

def conqure(n, lst):
    if not any(1 in i for i in lst): #리스트에 1이 없으면
        lst_count.append(0) #lst_count에 0을 넣음
        return
    elif not any(0 in i for i in lst): #르스트에 0이 없으면
        lst_count.append(1) #lst_count에 1을 넣음
        return
    else:
        lst_0 = [] #리스트 2개를 만들어서
        lst_1 = []
        for i in lst:
            lst_0.append(i[:n//2]) #세로 반으로 나눠버림
            lst_1.append(i[n//2:]) #나머지 반
        conqure(n//2, lst_0[:n//2]) #그걸 또 반으로 나눔
        conqure(n//2, lst_0[n//2:])
        conqure(n//2, lst_1[:n//2])
        conqure(n//2, lst_1[n//2:])
        return
    
lst_count = [] #함수안에서 0과 1을 넣을 리스트
conqure(n, lst) #함수 호출
print(lst_count.count(0)) #0의 개수 카운트
print(lst_count.count(1)) #1의 개수 카운트