이진 탐색 트리를 구현하기에 앞서 기본적인 트리의 구현을 해보려 합니다.
오늘 구현할 트리는 별도의 기능을 갖지 않고 트리의 순회를 중점적으로 보려 합니다.
순회란 트리를 돌면서 어떤 원소가 있는지 확인하는 작업을 말합니다.
이 때 어느 원소를 먼저 보는지에 따라 순회의 종류가 달라집니다.
트리의 순회는 재귀 방법으로 쉽게 구현할 수 있습니다.
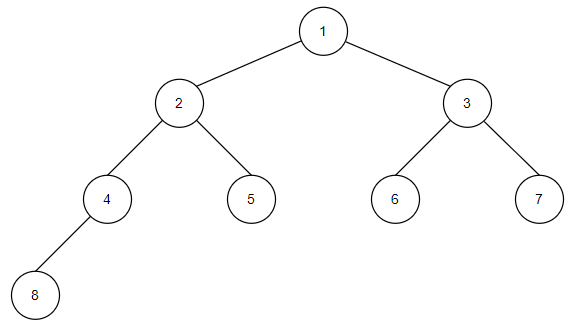
트리의 구조
class Node(object):
def __init__(self, item):
self.item = item
self.left = self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None-
Node class에서 item원소는 루트(노드)가 갖는 값을 저장하는 변수
-
left와 right는 각각 루트의 자식 노드를 가리킵니다
-
BinaryTree class는 빈 root만을 갖고 Node원소로 초기화 시켜줍니다
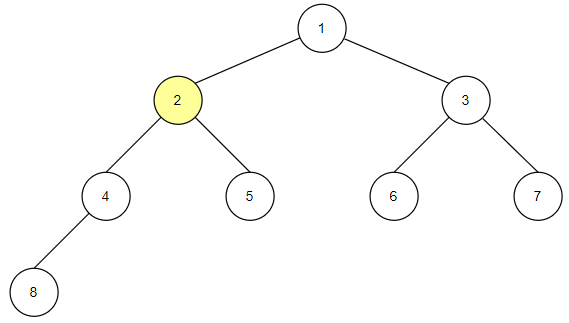
전위순회
-
전위 순회는 자식 노드를 확인하기 전에 서브 트리의 루트를 먼저 확인한 후에 자식 노드를 확인하는 순회 방법입니다.
-
자식 노드를 확인할 때는 왼쪽 노드부터 확인합니다.
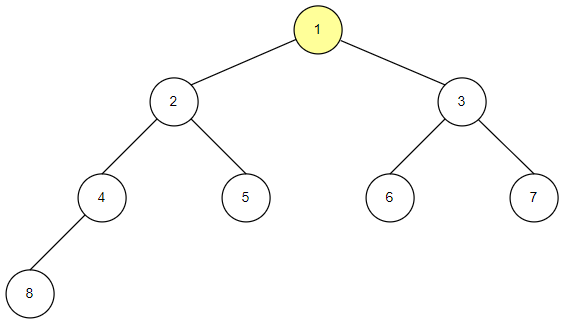
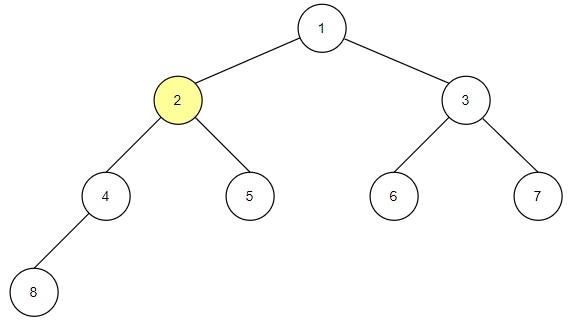
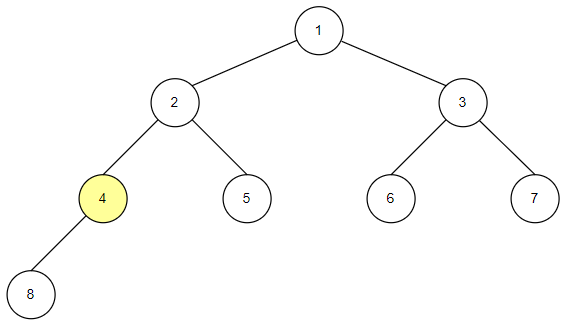
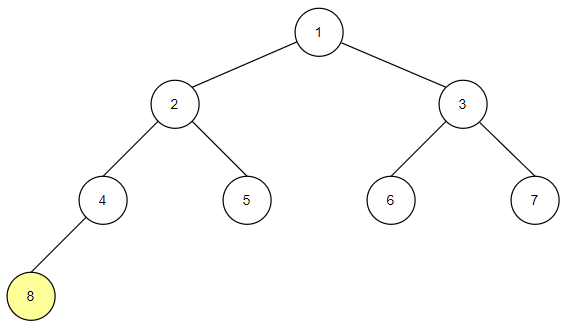
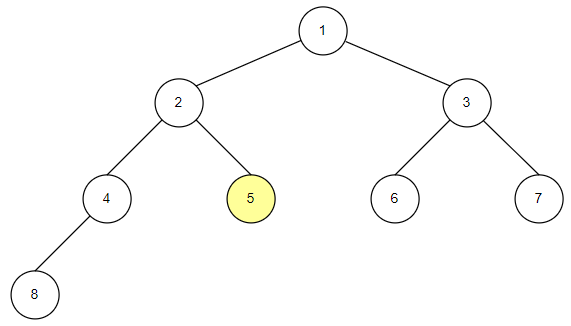
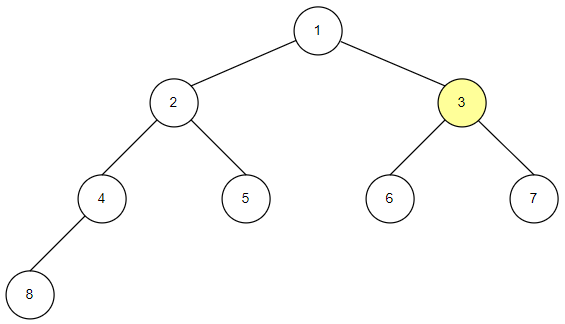
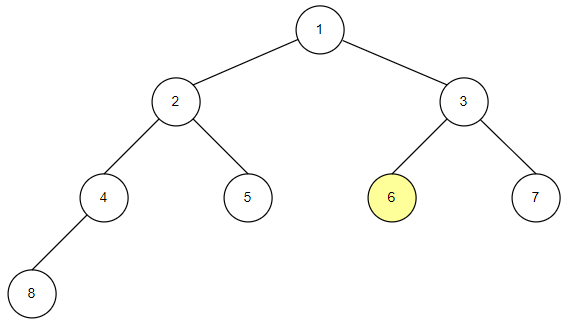
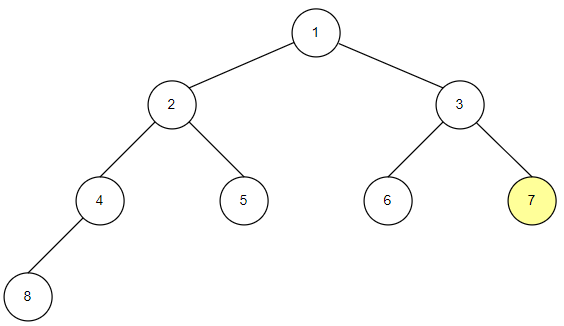
전위 순회의 구현
def preorder(self):
def _preorder(node):
print(node.item, end=' ')
if node.left:
_preorder(node.left)
if node.right:
_preorder(node.right)
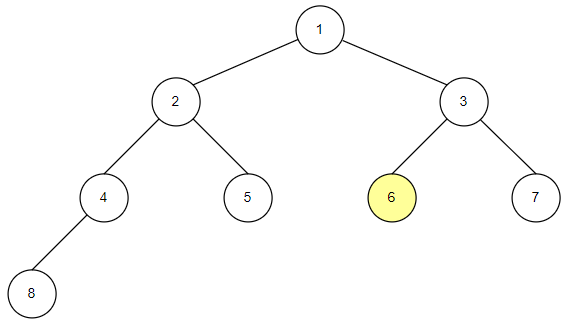
_preorder(self.root)중위순회
-
중위순회는 왼쪽 자식 노드, 루트 노드, 오른쪽 자식 노드 순으로 값을 확인하는 방식입니다.
-
자식 노드를 확인하고 밑에 자손 노드들이 있다면 자손 노드들도 동일한 방식으로 확인합니다.
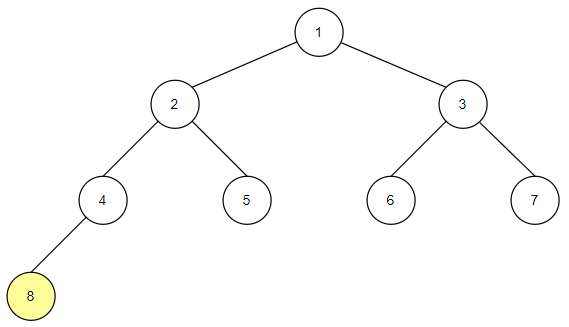
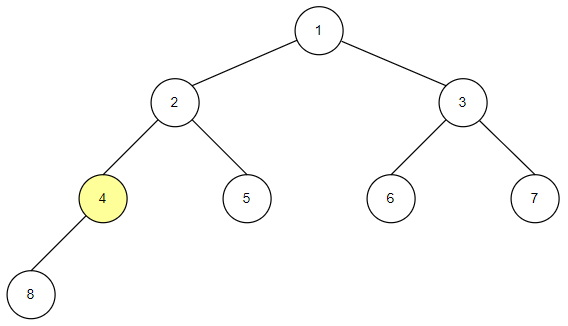
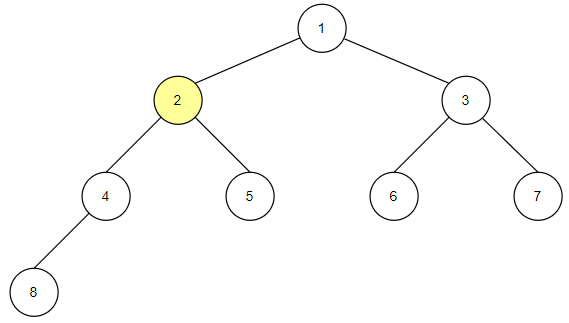
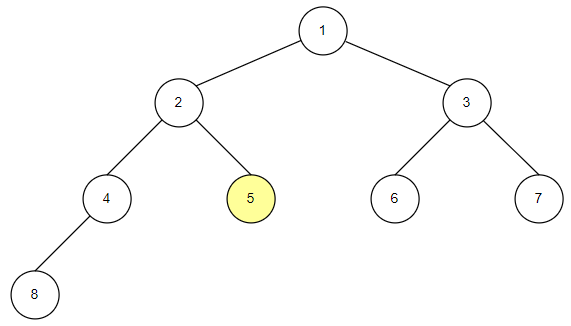
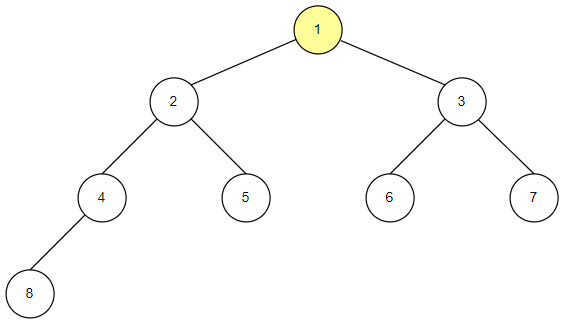
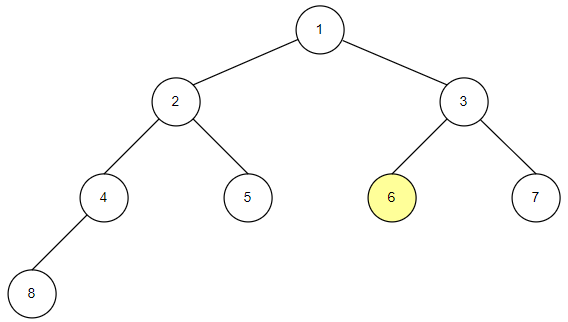
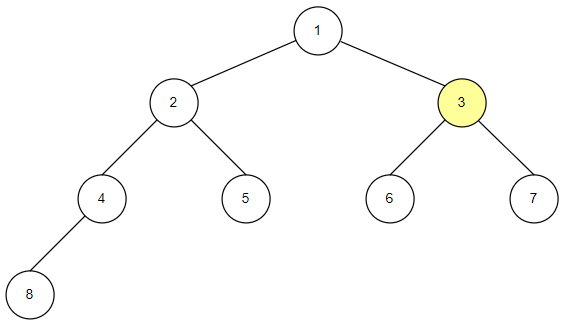
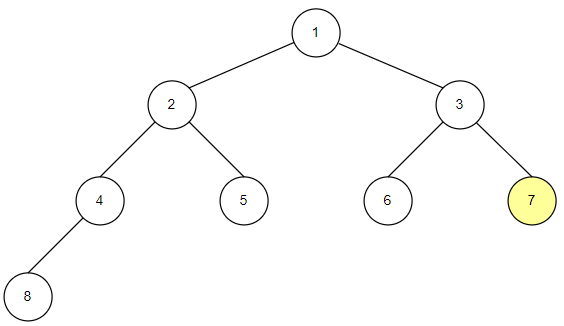
중위 순회의 구현
def inorder(self):
def _inorder(node):
if node.left:
_inorder(node.left)
print(node.item, end=' ')
if node.right:
_inorder(node.right)
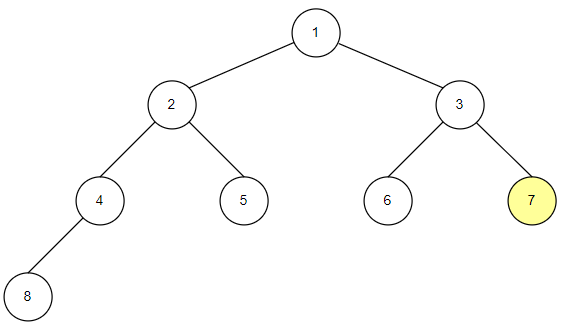
_inorder(self.root)후위 순회
-
후위 순회는 자식 노드를 모두 확인한 후에 루트 노드를 확인하는 순회 방법입니다.
-
자식 노드의 자손 노드가 존재한다면 동일한 방식으로 모두 확인합니다.
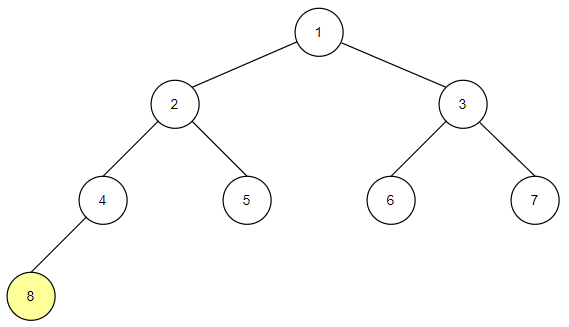
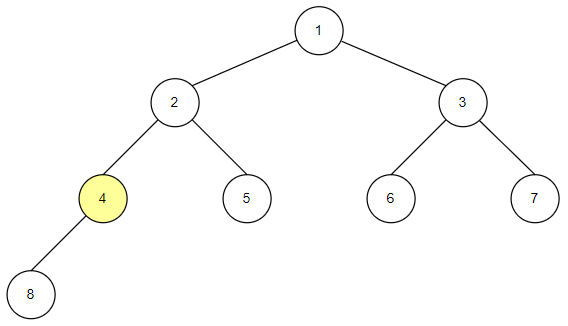
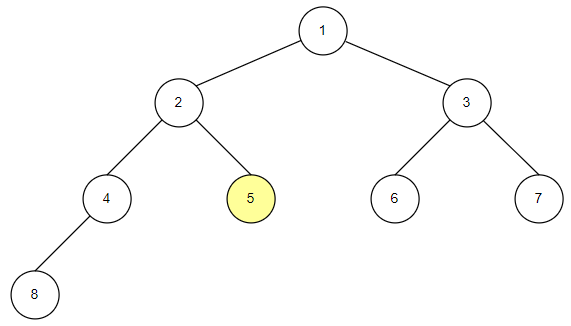
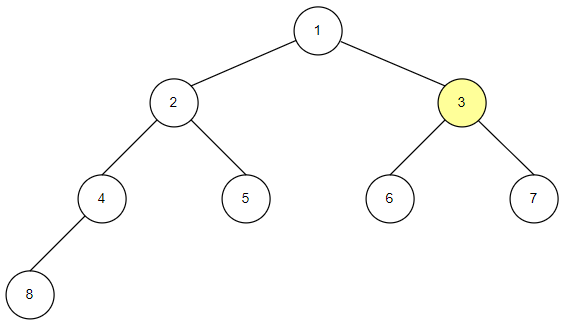
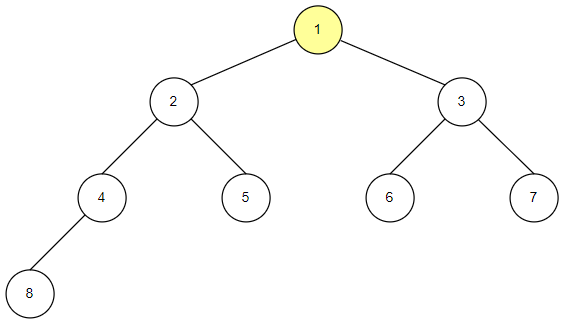
전체 코드
from collections import deque
class Node(object):
def __init__(self, item):
self.item = item
self.left = self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
def preorder(self):
def _preorder(node):
print(node.item, end=' ')
if node.left:
_preorder(node.left)
if node.right:
_preorder(node.right)
_preorder(self.root)
def inorder(self):
def _inorder(node):
if node.left:
_inorder(node.left)
print(node.item, end=' ')
if node.right:
_inorder(node.right)
_inorder(self.root)
def postorder(self):
def _postorder(node):
if node.left:
_postorder(node.left)
if node.right:
_postorder(node.right)
print(node.item, end=' ')
_postorder(self.root)
def levelorder(self):
q = deque([self.root])
while q:
node = q.popleft()
print(node.item, end=' ')
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
BT = BinaryTree()
N1 = Node(1)
N2 = Node(2)
N3 = Node(3)
N4 = Node(4)
N5 = Node(5)
N6 = Node(6)
N7 = Node(7)
N8 = Node(8)
BT.root = N1
N1.left = N2
N1.right = N3
N2.left = N4
N2.right = N5
N3.left = N6
N3.right = N7
N4.left = N8
print('preorder')
BT.preorder()
print('\ninorder')
BT.inorder()
print('\npostorder')
BT.postorder()
print('\nlevelorder')
BT.levelorder()백준에 이진 트리를 이용한 문제가 있어서 풀어봤습니다.
이진 검색 트리
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 256 MB 32158 12500 8804 37.883%
문제
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.
예제 입력 1
50
30
24
5
28
45
98
52
60
예제 출력 1
5
28
24
45
30
60
52
98
50
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
num_list = []
while True:
try:
num = int(input())
num_list.append(num)
except:
break
def postorder(first, end):
if first > end:
return
mid = end + 1 # 루트보다 큰 값이 존재하지 않을 경우를 대비
for i in range(first + 1, end + 1):
if num_list[first] < num_list[i]:
mid = i
break
postorder(first + 1, mid - 1)
postorder(mid, end)
print(num_list[first])
postorder(0, len(num_list) - 1)