어제에 이어서 DFS에 대하여 조금 더 공부해보기로 해서 DFS를 이용하는 백준 문제를 풀어보기로 했습니다.
문제 링크
트리의 부모 찾기
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 256 MB 59505 26193 18564 42.197%
문제
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 트리 상에서 연결된 두 정점이 주어진다.
출력
첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.
예제 입력 1
7
1 6
6 3
3 5
4 1
2 4
4 7
예제 출력 1
4
6
1
3
1
4
예제 입력 2
12
1 2
1 3
2 4
3 5
3 6
4 7
4 8
5 9
5 10
6 11
6 12
예제 출력 2
1
1
2
3
3
4
4
5
5
6
6
출처
문제를 만든 사람: baekjoon
잘못된 조건을 찾은 사람: jh05013
알고리즘 분류
그래프 이론
그래프 탐색
트리
너비 우선 탐색
깊이 우선 탐색
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
nums.append([i, v])
dfs(graph, i, visited)
n = int(input())
nums = []
graph = [[] for _ in range(n+1)] # 각 노드에 대한 인접 리스트
for _ in range(n-1):
a, b = map(int, input().split())
graph[a].append(b) # a와 b 사이에 간선 추가
graph[b].append(a) # 양방향 그래프이므로 b와 a 사이에도 간선 추가
# 방문처리
visited = [False] * (n+1)
dfs(graph, 1, visited)
nums.sort()
for i in range(n - 1):
print(nums[i][1])연산자 끼워넣기
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 512 MB 83584 43670 27799 49.433%
문제
N개의 수로 이루어진 수열 A1, A2, ..., AN이 주어진다. 또, 수와 수 사이에 끼워넣을 수 있는 N-1개의 연산자가 주어진다. 연산자는 덧셈(+), 뺄셈(-), 곱셈(×), 나눗셈(÷)으로만 이루어져 있다.
우리는 수와 수 사이에 연산자를 하나씩 넣어서, 수식을 하나 만들 수 있다. 이때, 주어진 수의 순서를 바꾸면 안 된다.
예를 들어, 6개의 수로 이루어진 수열이 1, 2, 3, 4, 5, 6이고, 주어진 연산자가 덧셈(+) 2개, 뺄셈(-) 1개, 곱셈(×) 1개, 나눗셈(÷) 1개인 경우에는 총 60가지의 식을 만들 수 있다. 예를 들어, 아래와 같은 식을 만들 수 있다.
1+2+3-4×5÷6
1÷2+3+4-5×6
1+2÷3×4-5+6
1÷2×3-4+5+6
식의 계산은 연산자 우선 순위를 무시하고 앞에서부터 진행해야 한다. 또, 나눗셈은 정수 나눗셈으로 몫만 취한다. 음수를 양수로 나눌 때는 C++14의 기준을 따른다. 즉, 양수로 바꾼 뒤 몫을 취하고, 그 몫을 음수로 바꾼 것과 같다. 이에 따라서, 위의 식 4개의 결과를 계산해보면 아래와 같다.
1+2+3-4×5÷6 = 1
1÷2+3+4-5×6 = 12
1+2÷3×4-5+6 = 5
1÷2×3-4+5+6 = 7
N개의 수와 N-1개의 연산자가 주어졌을 때, 만들 수 있는 식의 결과가 최대인 것과 최소인 것을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱셈(×)의 개수, 나눗셈(÷)의 개수이다.
출력
첫째 줄에 만들 수 있는 식의 결과의 최댓값을, 둘째 줄에는 최솟값을 출력한다. 연산자를 어떻게 끼워넣어도 항상 -10억보다 크거나 같고, 10억보다 작거나 같은 결과가 나오는 입력만 주어진다. 또한, 앞에서부터 계산했을 때, 중간에 계산되는 식의 결과도 항상 -10억보다 크거나 같고, 10억보다 작거나 같다.
예제 입력 1
2
5 6
0 0 1 0
예제 출력 1
30
30
예제 입력 2
3
3 4 5
1 0 1 0
예제 출력 2
35
17
예제 입력 3
6
1 2 3 4 5 6
2 1 1 1
예제 출력 3
54
-24
힌트
세 번째 예제의 경우에 다음과 같은 식이 최댓값/최솟값이 나온다.
최댓값: 1-2÷3+4+5×6
최솟값: 1+2+3÷4-5×6
출처
문제를 만든 사람: baekjoon
문제의 오타를 찾은 사람: jh05013, mwy3055
알고리즘 분류
브루트포스 알고리즘
백트래킹
빙산
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 256 MB 60985 17234 11422 25.726%
문제
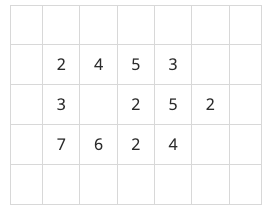
지구 온난화로 인하여 북극의 빙산이 녹고 있다. 빙산을 그림 1과 같이 2차원 배열에 표시한다고 하자. 빙산의 각 부분별 높이 정보는 배열의 각 칸에 양의 정수로 저장된다. 빙산 이외의 바다에 해당되는 칸에는 0이 저장된다. 그림 1에서 빈칸은 모두 0으로 채워져 있다고 생각한다.
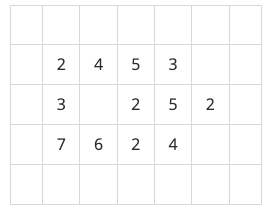
그림 1. 행의 개수가 5이고 열의 개수가 7인 2차원 배열에 저장된 빙산의 높이 정보
빙산의 높이는 바닷물에 많이 접해있는 부분에서 더 빨리 줄어들기 때문에, 배열에서 빙산의 각 부분에 해당되는 칸에 있는 높이는 일년마다 그 칸에 동서남북 네 방향으로 붙어있는 0이 저장된 칸의 개수만큼 줄어든다. 단, 각 칸에 저장된 높이는 0보다 더 줄어들지 않는다. 바닷물은 호수처럼 빙산에 둘러싸여 있을 수도 있다. 따라서 그림 1의 빙산은 일년후에 그림 2와 같이 변형된다.
그림 3은 그림 1의 빙산이 2년 후에 변한 모습을 보여준다. 2차원 배열에서 동서남북 방향으로 붙어있는 칸들은 서로 연결되어 있다고 말한다. 따라서 그림 2의 빙산은 한 덩어리이지만, 그림 3의 빙산은 세 덩어리로 분리되어 있다.
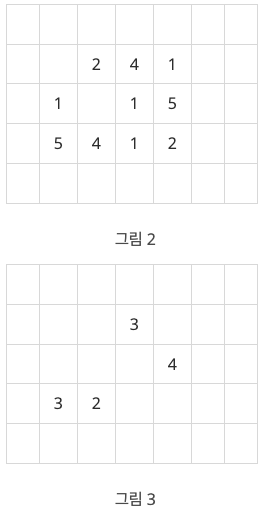
한 덩어리의 빙산이 주어질 때, 이 빙산이 두 덩어리 이상으로 분리되는 최초의 시간(년)을 구하는 프로그램을 작성하시오. 그림 1의 빙산에 대해서는 2가 답이다. 만일 전부 다 녹을 때까지 두 덩어리 이상으로 분리되지 않으면 프로그램은 0을 출력한다.
입력
첫 줄에는 이차원 배열의 행의 개수와 열의 개수를 나타내는 두 정수 N과 M이 한 개의 빈칸을 사이에 두고 주어진다. N과 M은 3 이상 300 이하이다. 그 다음 N개의 줄에는 각 줄마다 배열의 각 행을 나타내는 M개의 정수가 한 개의 빈 칸을 사이에 두고 주어진다. 각 칸에 들어가는 값은 0 이상 10 이하이다. 배열에서 빙산이 차지하는 칸의 개수, 즉, 1 이상의 정수가 들어가는 칸의 개수는 10,000 개 이하이다. 배열의 첫 번째 행과 열, 마지막 행과 열에는 항상 0으로 채워진다.
출력
첫 줄에 빙산이 분리되는 최초의 시간(년)을 출력한다. 만일 빙산이 다 녹을 때까지 분리되지 않으면 0을 출력한다.
예제 입력 1
5 7
0 0 0 0 0 0 0
0 2 4 5 3 0 0
0 3 0 2 5 2 0
0 7 6 2 4 0 0
0 0 0 0 0 0 0
예제 출력 1
2
출처
Olympiad > 한국정보올림피아드 > KOI 2006 > 초등부 2번
잘못된 데이터를 찾은 사람: occidere, zayne
알고리즘 분류
구현
그래프 이론
그래프 탐색
너비 우선 탐색
깊이 우선 탐색
import sys
sys.setrecursionlimit(10**5)
input = sys.stdin.readline
def dfs(i, j):#2가지 경우로 나뉘는걸 체크해주기 위한 함수.
for k in range(4): # 상하좌우 4방향에 대해 탐색
nx = dx[k] + i # 새로운 좌표 탐색
ny = dy[k]+j
if 0 <= nx < n and 0 <= ny < m and vist[nx][ny]: # 새로운 좌표가 범위 안에 있고 방문하지 않은 좌표라면
vist[nx][ny] = False # 방문 표시
if s[nx][ny] != 0: # 새로운 좌표가 0이 아니라면
dfs(nx,ny) # 새로운 좌표로 dfs 재귀 호출
input = sys.stdin.readline
n,m = map(int,input().split())
s=[list(map(int,input().split())) for _ in range(n)]
dx = [1, -1, 0, 0] #상하좌우 이동
dy = [0, 0, 1, -1]
vist = [[False] * m for _ in range(n)] # 방문 체크
t = 0
while True:
t += 1 # 연도 + 1
for i in range(n):
for j in range(m):
if s[i][j] != 0: # 빙산 위치
vist[i][j] = True # 방문 표시
c = s[i][j] # 빙산 높이 저장
for k in range(4): # 상하좌우 네 방향 반복문
nx = dx[k] + i # 상하좌우 힌 칸 이동한 새로운 위치를 계산
ny = dy[k] + j
if 0 <= nx < n and 0 <= ny < m and not vist[nx][ny]: # 새로운 위치가 범위 안에 있고, 방문하지 않은 곳이라면
if s[nx][ny] == 0: # 새로운 위치가 바다면
c -= 1 # 빙산 높이 - 1
if c == 0: # 빙산 높이가 0이 되면 탐색 종료
break
s[i][j] = c # 감소된 빙산 높이 저장
count=0#영역의 개수
for i in range(n):
for j in range(m):
if s[i][j] != 0 and vist[i][j]: # 해당 칸이 얼음이고 방문하지 않았으면
dfs(i,j) # 현제 위치에서 dfs함수 호출
count += 1 # count에 1을 더함
elif s[i][j] == 0 and vist[i][j]: # 해당 칸이 바다이고 방문하지 않았으면
vist[i][j] = False # 방문 처리
if count >= 2:#영역이 2개 이상으로 나뉜경우니 출력해주고 반복문을 탈출한다.
print(t) # 연도를 출력
break
elif count == 0:#한번에 녹았다는 의미이므로 0을 출력해주고 반복문을 탈출한다.
print(0)
break오늘 DFS를 활용한 문제를 풀어보면서 DFS의 활용도 부족하지만, 재귀함수에 대해서도 더 공부가 필요하겠다고 느꼈습니다.
크래프톤 정글의 빡빡한 일정 속에서는 내가 부족한 부분에 대해 더 공부할 시간이 많지 않아 아쉽지만, 1~4주차 알고리즘 공부가 끝나도 하루에 한 문제씩 꾸준히 풀면서 부족한 부분을 채워야겠다고 생각되는 하루였습니다 :)