오늘은 다익스트라 알고리즘을 공부하고, 부족하다고 생각한 BFS문제를 조금 풀어봤습니다.
최단 경로 알고리즘
가장 짧은 경로를 찾는 알고리즘이다. 그래서 '길찾기'문제라고도 불린다. 학부 수준에서 사용하는 최단 거리 알고리즘은 다익스트라 최단 경로 알고리즘, 플로이드 워셜, 벨만 포드 알고리즘 이렇게 3가지이다. 이 중 다익스트라 최단 경로 알고리즘을 이번 포스팅에서 다뤄보려고 한다.
다익스트라 최단 경로 알고리즘
하나의 출발 노드로 부터 다른 모든 노드까지의 최단거리를 구하는 알고리즘이다. 단, '음의 간선'이 없을 때만 정상적으로 동작한다. 다익스트라가 연구한 알고리즘 중 가장 대표적인 알고리즘이기 때문에 간단하게 다익스트라 알고리즘이라고도 불린다. 다익스트라 알고리즘은 기본적으로 그리디 알고리즘으로 분류된다. 매번 가장 비용이 가장 적은 노드를 선택하는 과정을 반복하기 때문이다.
다익스트라 알고리즘 동작과정
1.출발 노드를 설정한다
2.최단거리 테이블을 초기화한다.
-> 다른 모든 노드로 가는 최단거리를 '무한'으로 초기화한다
3.방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드를 선택한다.
-> 이때 선택된 노드의 최단거리는 확정된다.
4.해당 노드를 거쳐 다른 노드로 가는 비용를 게산하여 최단 거리 테이블을 갱신한다.
- 3~4 과정을 반복한다.
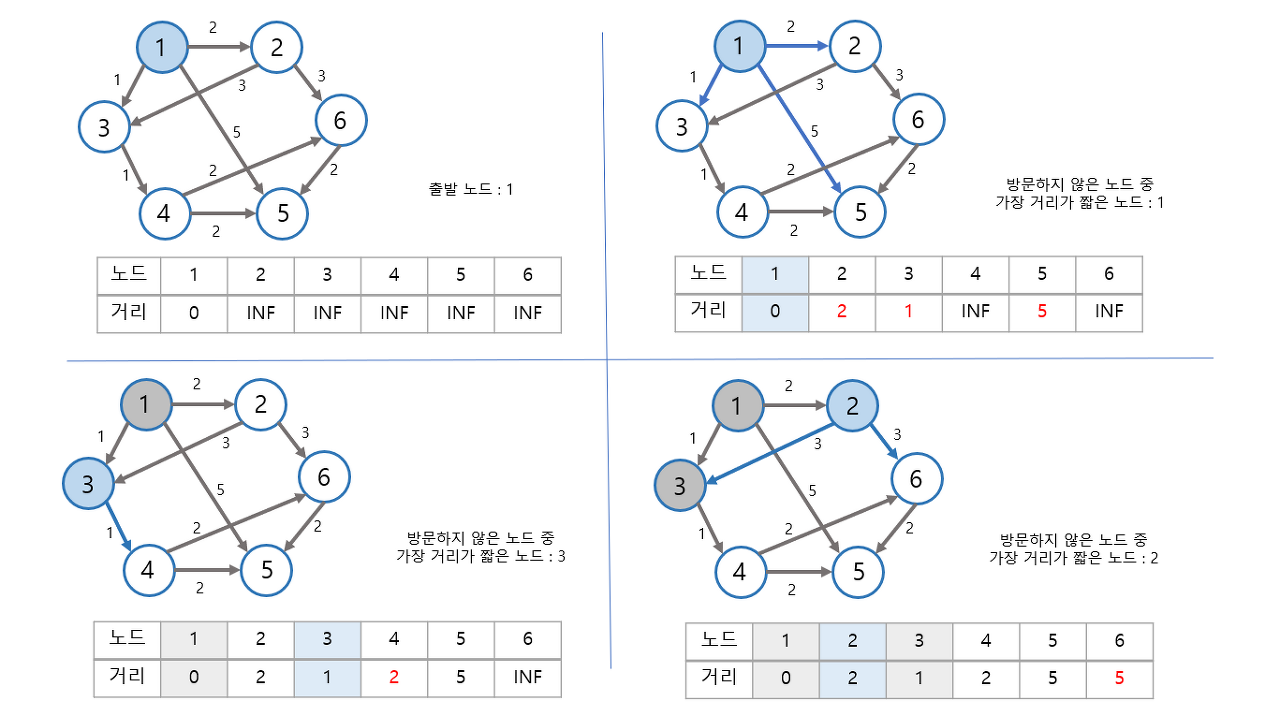
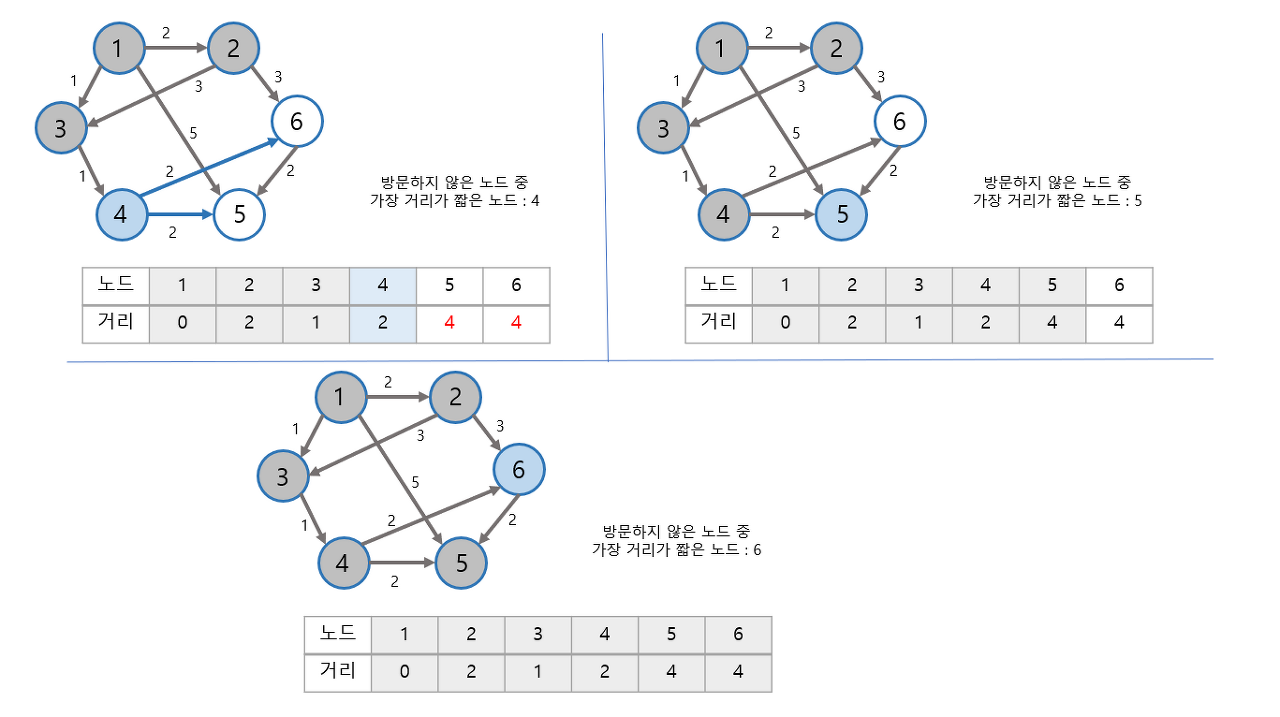
다익스트라 알고리즘 : 순차탐색
방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 순차 탐색을 이용하여 코드로 구현할 수 있다. 이때 시간복잡도는 O(N^2)이다. 총 O(N)번에 걸쳐 가장 짧은 노드를 매번 선형탐색해야하고 현재 노드와 연결된 노드를 매번 일일히 확인해야하기 때문이다. 따라서 전체 노드의 수가 5,000개 이하라면 순차탐색 방법을 써도 괜찮지만 그 이상이라면 힙을 사용하는 개선된 다익스트라 알고리즘을 이용해야한다.
import sys
input = sys.stdin.readline # 빠른 입력
INF = int(1e9) # 무한을 의미하는 값으로 10억 설정
# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 방문 체크
visited = [False]*(n+1)
# 최단거리 테이블
distance = [INF]*(n+1)
# 노드 연결정보
graph = [[] for i in range(n+1)]
for _ in range(m):
# a번노드에서 b번 노드로 가는 비용c
a,b,c = map(int, input().split())
graph[a].append((b,c))
# 방문하지 않은 노드 중 가장 최단거리가 짧은 노드의 번호를 반환
def get_smallest_node():
min_value = INF
index = 0
for i in range(1, n+1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
# 다익스트라 알고리즘
def dijkstra(start):
# 시작 노드
distance[start] = 0
visited[start] = True
# 출발노드와 인접노드에 대해 최단거리 테이블 갱신
for j in graph[start]:
distance[j[0]] = j[1]
# 모든 노드에 대해 반복
for i in range(n-1):
# 현재 최단거리가 가장 짧은 노드를 꺼내서 방문처리
now = get_smallest_node()
visited[now] = True
# 선택된 노드와 연결된 다른 노드를 확인
for j in graph[now]:
# 선택된 노드를 통해 가는 비용을 다시 계산
# 선택된 노드의 비용 + 연결된 노드로 가는 비용
cost = distance[now] + j[1]
# 선택된 노드를 거쳐서 가는 비용이 더 짧은 경우
if cost<distance[j[0]]:
distance[j[0]] = cost # 최단거리 테이블 갱신
#다익스트라 알고리즘수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n+1):
# 도달할 수 없는 경우
if distance[i] == INF:
print("infinity")
else:
print(distance[i])다익스트라 알고리즘 : 최소힙
방문하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택하기 위해 최소 힙을 사용한다.
파이썬의 heapq라이브러리는 원소로 튜플을 받으면 튜플의 첫번째 원소를 기준으로 우선순위 큐를 구성한다. 따라서 (거리, 노드 번호) 순서대로 튜플 데이터를 구성해 우선순위 큐에 넣으면 거리순으로 정렬된다. 힙에서 노드를 꺼냈는데 만약 해당 노드를 이미 처리한적이 있다면 무시하고 아직 처리하지 않은 노드에 대해서만 처리하면된다.
import heapq
import sys
input = sys.stdin.readline # 빠른 입력
INF = int(1e9) # 무한을 의미하는 값으로 10억 설정
# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 최단거리 테이블
distance = [INF]*(n+1)
# 노드 연결정보
graph = [[] for i in range(n+1)]
for _ in range(m):
# a번노드에서 b번 노드로 가는 비용c
a,b,c = map(int, input().split())
graph[a].append((b,c))
# 다익스트라 알고리즘(최소힙 이용))
def dijkstra(start):
q=[]
# 시작 노드
heapq.heappush(q, (0,start))
distance[start] = 0
while q:
# 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 이미 처리된 노드였다면 무시
# 별도의 visited 테이블이 필요없이, 최단거리테이블을 이용해 방문여부 확인
if distance[now] < dist:
continue
# 선택된 노드와 인접한 노드를 확인
for i in graph[now]:
cost = dist + i[1]
# 선택된 노드를 거쳐서 이동하는 것이 더 빠른 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost,i[0]))
# 다익스트라 알고리즘수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n+1):
# 도달할 수 없는 경우
if distance[i] == INF:
print("infinity")
else:
print(distance[i])다익스트라를 활용한 문제
문제 링크
특정 거리의 도시 찾기
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 256 MB 38421 12051 7614 29.486%
문제
어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.
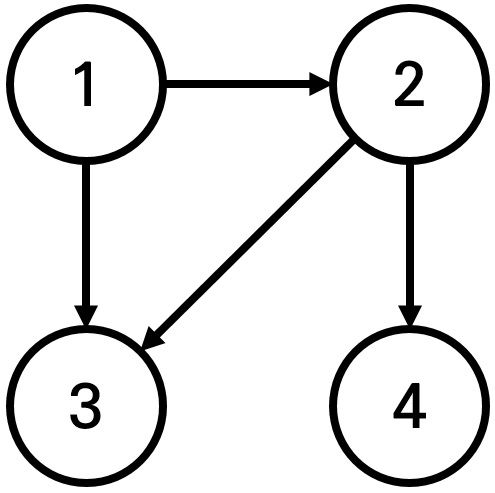
예를 들어 N=4, K=2, X=1일 때 다음과 같이 그래프가 구성되어 있다고 가정하자.
이 때 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
입력
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다. (1 ≤ A, B ≤ N) 단, A와 B는 서로 다른 자연수이다.
출력
X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.
이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.
예제 입력 1
4 4 2 1
1 2
1 3
2 3
2 4
예제 출력 1
4
예제 입력 2
4 3 2 1
1 2
1 3
1 4
예제 출력 2
-1
예제 입력 3
4 4 1 1
1 2
1 3
2 3
2 4
예제 출력 3
2
3
출처
데이터를 추가한 사람: ajtwlstmdgks
문제를 만든 사람: ndb796
알고리즘 분류
그래프 이론
그래프 탐색
너비 우선 탐색
데이크스트라
import sys
from collections import deque
input = sys.stdin.readline
# BFS 메서드 정의
def bfs(start):
# 거리가 k인 도시들의 번호를 저장하기 위한 리스트
answer = []
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = True
# 출발점으로부터의 거리 초기화
distance[start] = 0
# 큐가 빌 떄까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력하기
now = queue.popleft()
# 아직 방문하지 않은 인접한 정점들을 큐에 삽입
for i in graph[now]:
if not visited[i]:
visited[i] = True
queue.append(i)
# 출발점으로부터의 거리 계산
distance[i] = distance[now] + 1
# 거리가 k인 도시를 answer 리스트에 추가
if distance[i] == k:
answer.append(i)
# 거리가 k인 도시가 없으면 -1 출력
if len(answer) == 0:
print(-1)
else:
# 오름차순으로 정렬하여 출력
answer.sort()
for i in answer:
print(i, end='\n')
# 입력 받기
n, m, k, x = map(int, input().split())
graph = [[] for _ in range(n+1)]
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b)
# 각 노드가 방문된 정보를 표현하는 리스트
visited = [False] * (n+1)
# 출발점으로부터의 거리를 저장하는 리스트
distance = [0] * (n+1)
# BFS 함수 호출
bfs(x)BFS문제도 하나 추가해보겠습니다.
문제 링크
미로 탐색
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 192 MB 159476 70383 45130 42.829%
문제
N×M크기의 배열로 표현되는 미로가 있다.
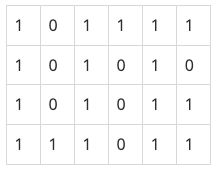
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
예제 입력 1
4 6
101111
101010
101011
111011
예제 출력 1
15
예제 입력 2
4 6
110110
110110
111111
111101
예제 출력 2
9
예제 입력 3
2 25
1011101110111011101110111
1110111011101110111011101
예제 출력 3
38
예제 입력 4
7 7
1011111
1110001
1000001
1000001
1000001
1000001
1111111
예제 출력 4
13
출처
데이터를 추가한 사람: djm03178, jh05013, poia0304, sait2000
알고리즘 분류
그래프 이론
그래프 탐색
너비 우선 탐색
import sys
from collections import deque
input = sys.stdin.readline
def bfs(x, y):
# 큐(queue) 구현을 위해 deque 라이브러리 사용
queue = deque()
queue.append((x, y))
# 큐가 빌 때까지 반복
while queue:
x, y = queue.popleft()
# 현제 방향에서 4가지 방향으로 위치 확인
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 미로 찾기 공간을 벗어난 경우 무시
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
# 벽인 경우 무시
if graph[nx][ny] == 0:
continue
# 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx, ny))
# 가장 오른쪽 아래까지의 최단 거리 반환
return graph[n - 1][m - 1]
# n, m을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입렵 받기
graph = []
for i in range(n):
a = list(map(int, input().strip()))
graph.append(a)
# 이동할 네 가지 방향 정의(상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# bfs를 수행한 결과 출력
print(bfs(0, 0))