위상 정렬
사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미
예시) 선수과목을 고려한 학습 순서 설정
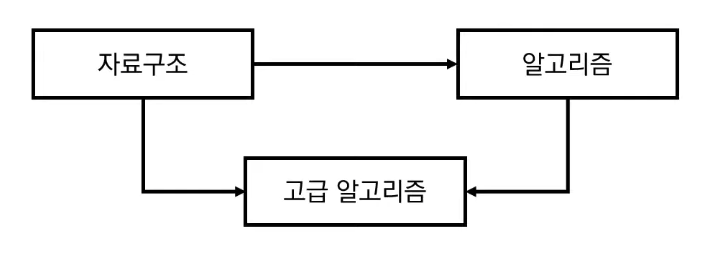
위 세 과목을 모두 듣기 위한 적절한 학습 순서는?
자료구조 → 알고리즘 → 고급 알고리즘 (O)
자료구조 → 고급 알고리즘 → 알고리즘 (X)
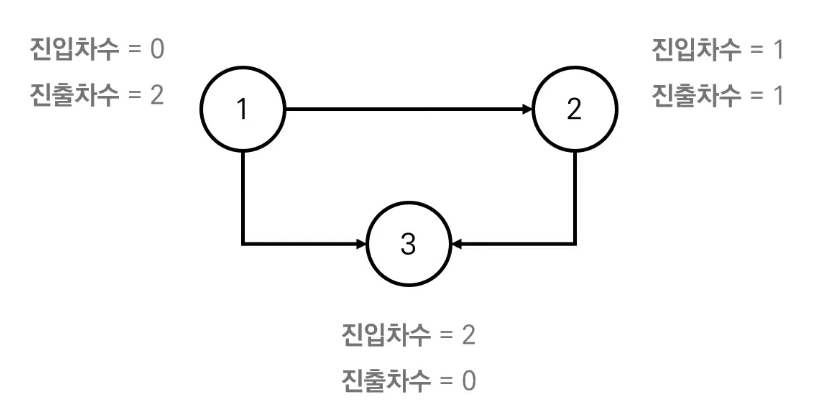
진입차수와 진출차수
진입차수(Indegree): 특정한 노드로 들어오는 간선의 개수
진출차수(Outdegree): 특정한 노드에서 나가는 간선의 개수
위상 정렬 알고리즘
큐를 이용하는 위상 정렬 알고리즘의 동작 과정은 다음과 같다
진입차수가 0인 모든 노드를 큐에 넣는다
큐가 빌 때까지 다음의 과정을 반복한다
큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다
새롭게 진입차수가 0이 된 노드를 큐에 넣는다
=> 결과 적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과와 같다
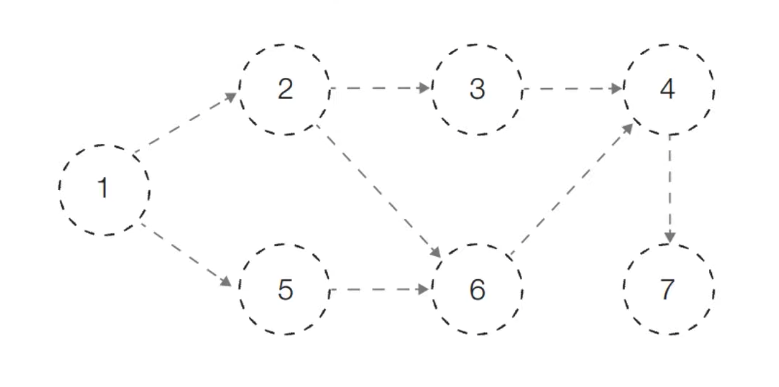
위상 정렬 동작 예시
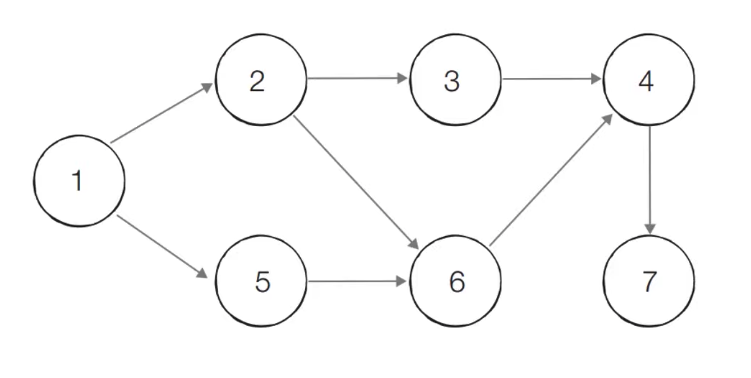
위상 정렬을 수행할 그래프를 준비한다
이때 그래프는 사이클이 없는 방향 그래프 (DAG)여야 한다
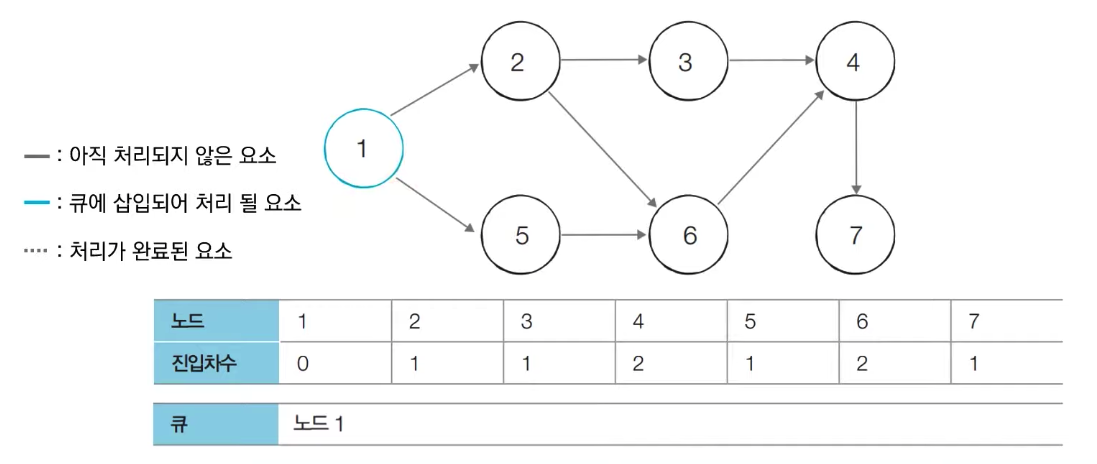
[초기 단계] 초기 단계에서는 진입차수가 0인 모든 노드를 큐에 넣는다
처음에 노드 1이 큐에 삽입된다
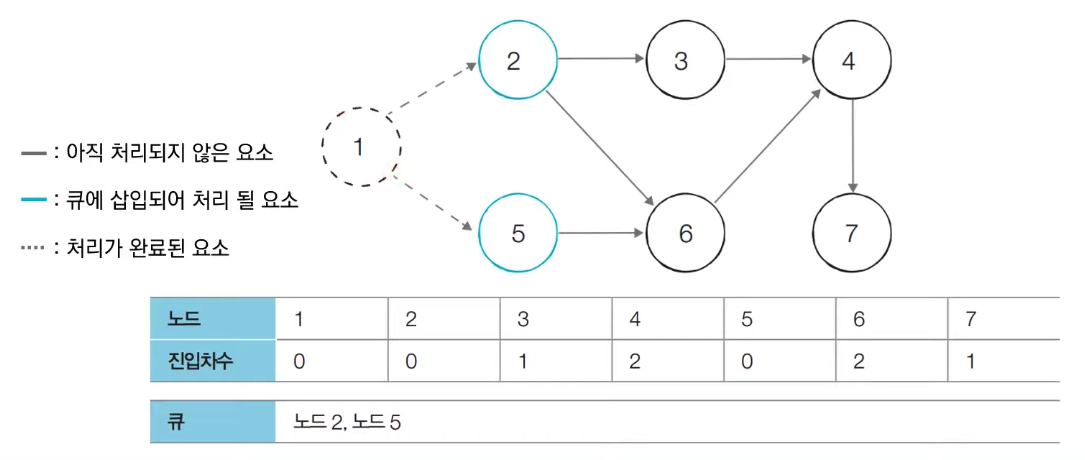
[Step 1] 큐에서 노드 1을 꺼낸 뒤에 노드 1에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
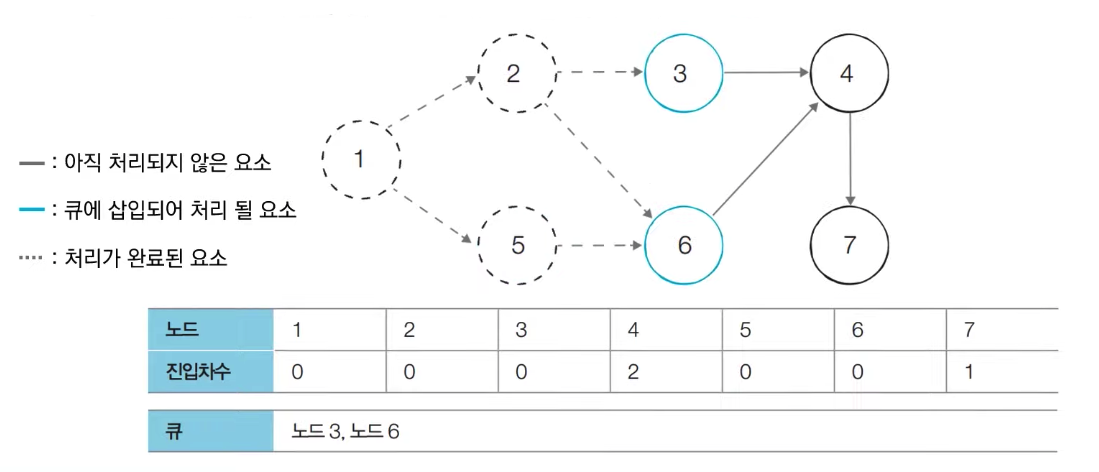
[Step 2] 큐에서 노드 2를 꺼낸 뒤에 노드 2에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
[Step 3] 큐에서 노드 5를 꺼낸 뒤에 노드 5에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
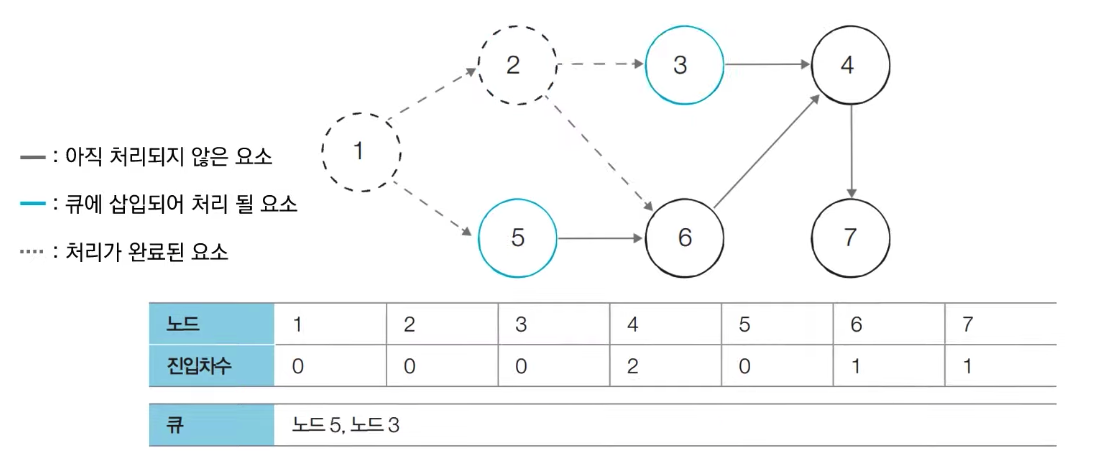
[Step 4] 큐에서 노드 3를 꺼낸 뒤에 노드 3에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
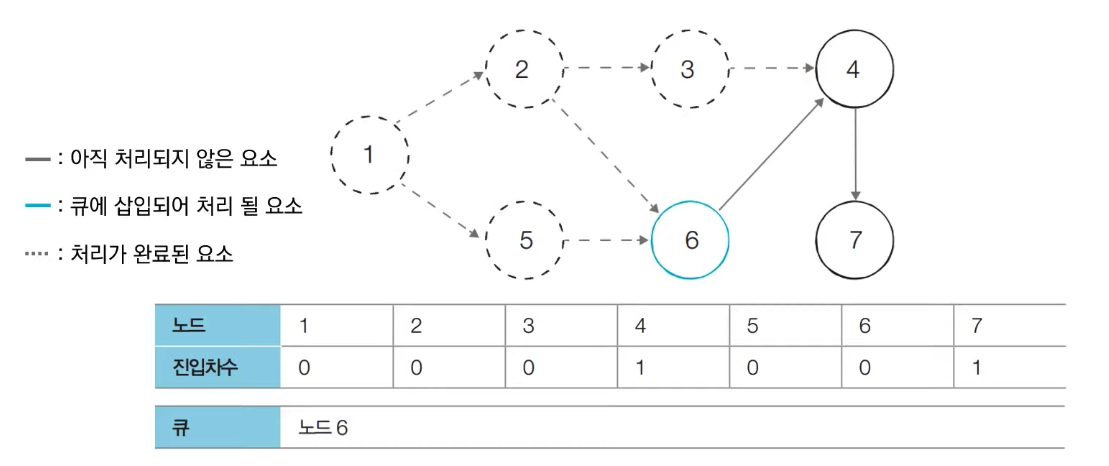
[Step 5] 큐에서 노드 6을 꺼낸 뒤에 노드 6에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
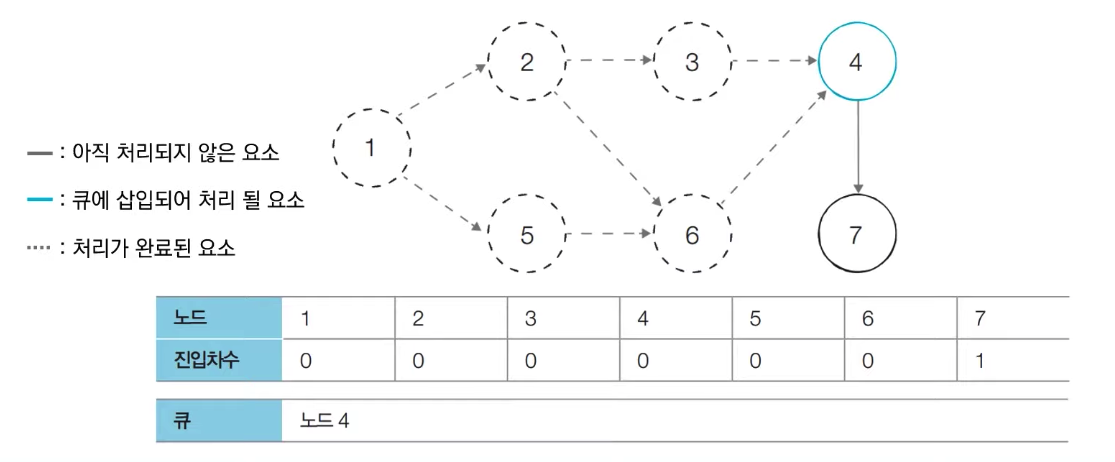
[Step 6] 큐에서 노드 4를 꺼낸 뒤에 노드 4에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
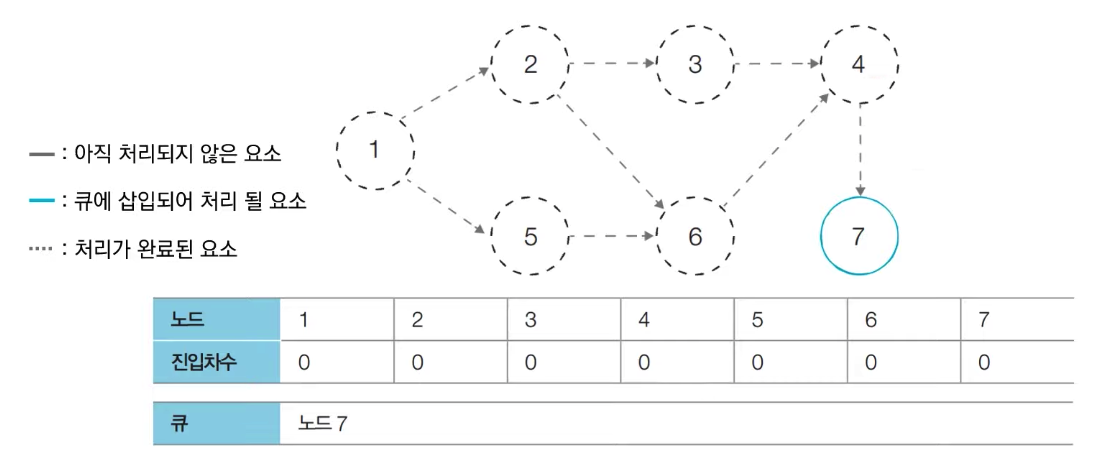
[Step 7] 큐에서 노드 7을 꺼낸 뒤에 노드 7에서 나가는 간선을 제거한다
새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다
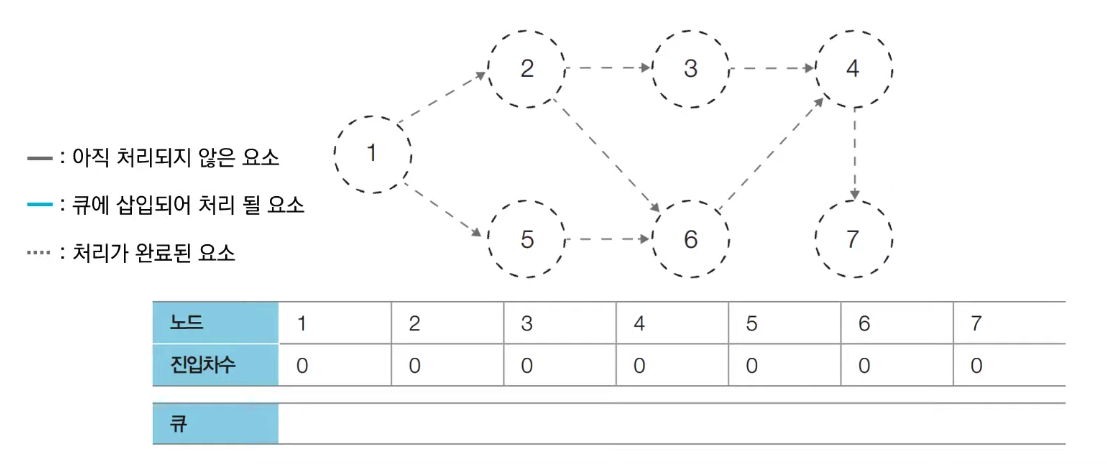
[위상 정렬 결과]
큐에 삽입된 전체 노드 순서: 1 → 2 → 5 → 3 → 6 → 4 → 7
위상 정렬의 특징
위상 정렬은 DAG에 대해서만 수행할 수 있다
DAG (Direct Acyclic Graph): 순환하지 않는 방향 그래프
위상 정렬에서는 여러 가지 답이 존재할 수 있다
한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면 여러 가지 답이 존재한다
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다
사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어가지 못한다
스택을 활용한 DFS를 이용해 위상 정렬을 수행할 수도 있다
위상 정렬 알고리즘 (Python)
from collections import deque
# 노드의 개수와 간선의 개수를 입력 받기
v, e = map(int, input().split())
# 모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for i in range(v + 1)]
# 방향 그래프의 모든 간선 정보를 입력 받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) # 정점 A에서 B로 이동 가능
# 진입 차수를 1 증가
indegree[b] += 1
# 위상 정렬 함수
def topology_sort():
result = [] # 알고리즘 수행 결과를 담을 리스트
q = deque() # 큐 기능을 위한 deque 라이브러리 사용
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
# 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')
topology_sort()입력 예시
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4출력 예시
1 2 5 3 6 4 7위상 정렬을 이용한 알고리즘 문제
줄 세우기
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 128 MB 39134 22742 15069 56.379%
문제
N명의 학생들을 키 순서대로 줄을 세우려고 한다. 각 학생의 키를 직접 재서 정렬하면 간단하겠지만, 마땅한 방법이 없어서 두 학생의 키를 비교하는 방법을 사용하기로 하였다. 그나마도 모든 학생들을 다 비교해 본 것이 아니고, 일부 학생들의 키만을 비교해 보았다.
일부 학생들의 키를 비교한 결과가 주어졌을 때, 줄을 세우는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의미이다.
학생들의 번호는 1번부터 N번이다.
출력
첫째 줄에 학생들을 앞에서부터 줄을 세운 결과를 출력한다. 답이 여러 가지인 경우에는 아무거나 출력한다.
예제 입력 1
3 2
1 3
2 3
예제 출력 1
1 2 3
예제 입력 2
4 2
4 2
3 1
예제 출력 2
4 2 3 1
출처
빠진 조건을 찾은 사람: indioindio
데이터를 추가한 사람: lhs456852, wlstn6278
알고리즘 분류
그래프 이론
위상 정렬
from collections import deque
# 노드의 개수와 간선의 개수를 입력 받기
v, e = map(int, input().split())
# 모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for i in range(v + 1)]
# 방향 그래프의 모든 간선 정보를 입력 받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) # 정점 A에서 B로 이동 가능
# 진입 차수를 1 증가
indegree[b] += 1
# 위상 정렬 함수
def topology_sort():
result = [] # 알고리즘 수행 결과를 담을 리스트
q = deque() # 큐 기능을 위한 deque 라이브러리 사용
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
# 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')
topology_sort()