5/2 누적합 알고리즘(Cumulative sum algorithm)

누적합 알고리즘(Cumulative sum algorithm)

누적합 알고리즘(Cumulative Sum Algorithm)은 주어진 배열에서 각 위치까지의 합을 미리 계산하여 배열에 저장해 놓는 알고리즘입니다. 이 알고리즘은 데이터를 미리 처리하여 쿼리에 대한 응답 속도를 빠르게 할 수 있습니다.

예를 들어, 주어진 배열이 [1, 2, 3, 4, 5]이라면, 누적합 배열은 [1, 3, 6, 10, 15]가 됩니다. 이 배열을 이용하면, 2번째부터 4번째까지의 합을 계산하는 쿼리를 빠르게 처리할 수 있습니다. 이때의 답은 누적합 배열에서 4번째 원소에서 1번째 원소를 빼면 9가 됩니다.

누적합 알고리즘은 보통 한 번의 전처리(pre-processing)로 수행되기 때문에, 이후에 수행되는 쿼리에 대한 응답 속도가 매우 빠릅니다. 따라서, 다양한 분야에서 활용되며, 특히 머신러닝에서 데이터 전처리(preprocessing)에 많이 사용됩니다.

누적합 알고리즘의 장단점

장점:

• 빠른 응답 속도: 누적합 배열을 한 번 생성해 놓으면, 이후에 수행되는 쿼리에 대한 응답 속도가 매우 빠릅니다. 즉, 전처리(pre-processing) 단계에서 시간을 소모하더라도, 이후에 수행되는 쿼리에 대한 응답 속도를 높일 수 있습니다.
• 간단한 구현: 누적합 알고리즘은 구현이 매우 간단합니다. 주어진 배열에서 각 위치까지의 합을 구하는 방법은 여러 가지가 있지만, 대부분의 경우에는 for 루프를 이용하여 간단하게 구현할 수 있습니다.

단점:

• 추가 메모리 사용: 누적합 배열을 생성하기 위해서는 추가적인 메모리가 필요합니다. 이는 배열의 크기가 클수록 더 많은 메모리를 요구하므로, 메모리 사용량을 고려해야 합니다.
• 배열 변경 어려움: 누적합 배열을 생성한 이후에는 배열을 변경할 수 없습니다. 따라서, 배열이 자주 변경되는 경우에는 누적합 알고리즘을 사용하기 어려울 수 있습니다.
• 계산 복잡도: 누적합 배열을 생성하는 과정에서는 배열의 크기에 비례하는 시간이 소요됩니다. 따라서, 배열의 크기가 매우 큰 경우에는 전처리(pre-processing) 단계에서 시간이 오래 걸릴 수 있습니다.

누적합 알고리즘을 활용한 문제를 풀어봤습니다.

문제 링크

구간 합 구하기 4

문제
수 N개가 주어졌을 때, i번째 수부터 j번째 수까지 합을 구하는 프로그램을 작성하시오.

입력
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j가 주어진다.

출력
총 M개의 줄에 입력으로 주어진 i번째 수부터 j번째 수까지 합을 출력한다.

제한
1 ≤ N ≤ 100,000
1 ≤ M ≤ 100,000
1 ≤ i ≤ j ≤ N

예제 입력 1
5 3
5 4 3 2 1
1 3
2 4
5 5

예제 출력 1
12
9
1

이 문제를 그냥 구현한다면 시간 초과에서 벗어나지 못할 것입니다
그래서 저는 result에 0을 n + 1만큼 채워두고 0번째 자리는 비워둔 채로 각 자릿수의 합을 하나씩 채워줬습니다
예제를 예시로 들자면 5, 4, 3, 2, 1이라는 숫자를 더해서 [0], [5], [9], [12], [14], [15] 이렇게 result를 채워주고 시작 번호와 끝 번호를 받으면 끝 번호의 인덱스에서 시작 번호 -1의 인덱스에 값을 빼주면 답이 나오게 코드를 짜봤습니다

import sys
input = sys.stdin.readline

n, m = map(int, input().split())

num = list(map(int, input().split()))
result = [0] * (n + 1)

k = 0
for i in range(n):
    k += num[i]
    result[i+1] = k

for j in range(m):
    a, b = map(int, input().split())
    anw = result[b] - result[a - 1]
    print(anw)

문제 링크

구간 합 구하기 5

문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

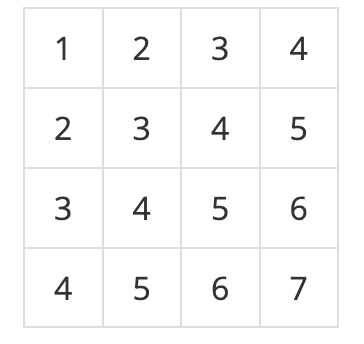
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.

입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)

출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.

예제 입력 1
4 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
2 2 3 4
3 4 3 4
1 1 4 4

예제 출력 1
27
6
64

예제 입력 2
2 4
1 2
3 4
1 1 1 1
1 2 1 2
2 1 2 1
2 2 2 2

예제 출력 2
1
2
3
4

이 문제는 위에 문제와 비슷하지만 2차원 배열을 사용한다는 점이 다릅니다
2차원 배열 문제를 풀 때 사용한 방법입니다

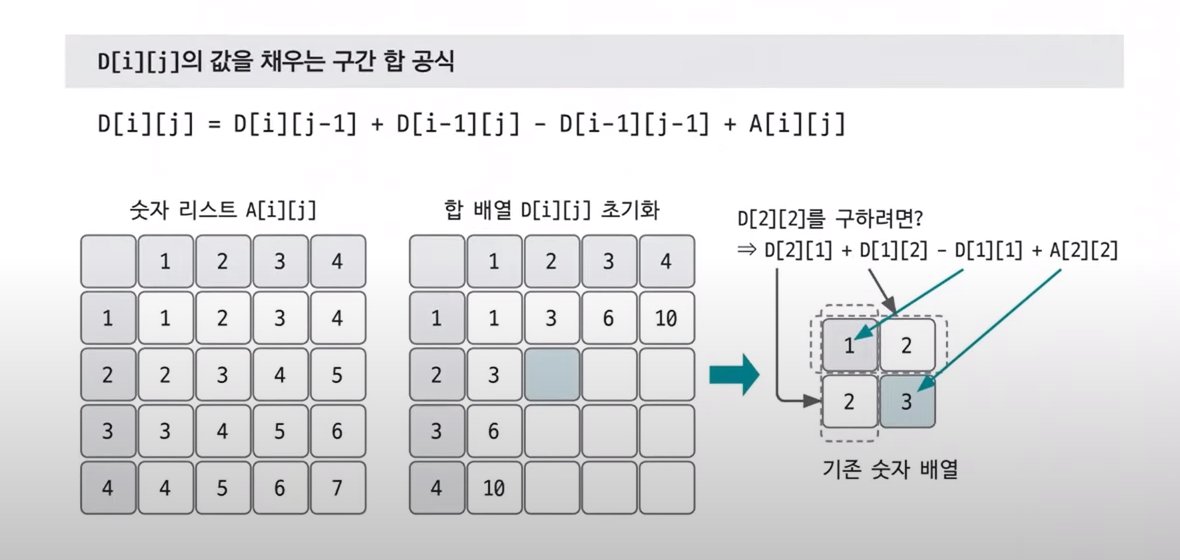
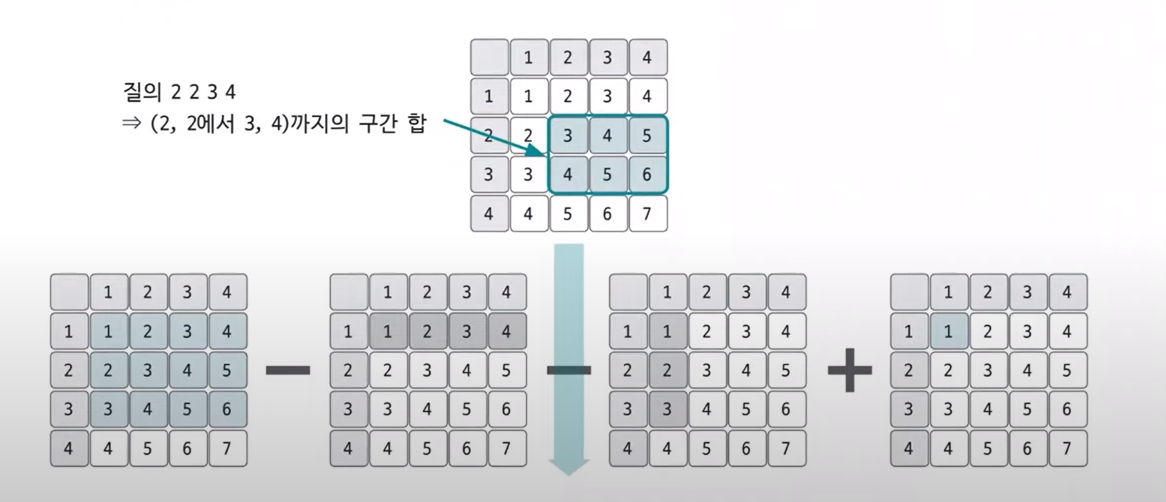
위에 사진의 방식으로 해결한 코드입니다

import sys
input = sys.stdin.readline

n, m = map(int, input().split())
result = [[0] * (n + 1) for _ in range(n + 1)]

k = 0
for i in range(1, n + 1):
    nums = list(map(int, input().split()))
    k = 0
    for j in range(1, n + 1):
        k += nums[j-1]
        result[i][j] = k + result[i-1][j]
        
for j in range(m):
    a, b, c, d = map(int, input().split())
    ans = result[c][d] - result[a-1][d] - result[c][b-1] + result[a-1][b-1]
    print(ans)

오늘 누적합에 관해서 공부하면서 시간 초과를 벗어날 수 있는 한 가지 방법을 알게 되어 좋았습니다
내일은 투 포인터, 슬라이딩 윈도우 알고리즘에 관해서 공부해볼 예정입니다