[BOJ] 9251번_LCS_DP (C++)

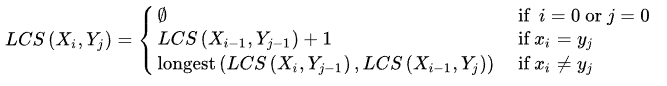
[문제]

https://www.acmicpc.net/problem/9251

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

첫째 줄과 둘째 줄에 두 문자열이 주어질 때, LCS의 길이를 출력하는 프로그램을 만드는 문제이다.

[사용 알고리즘]

DP(다이나믹 프로그래밍)

[풀이 핵심]

*해당 문제 풀이를 위해 아래 링크의 위키피디아를 참고했다.

https://ko.wikipedia.org/wiki/%EC%B5%9C%EC%9E%A5_%EA%B3%B5%ED%86%B5_%EB%B6%80%EB%B6%84_%EC%88%98%EC%97%B4

• LCS 함수를 정의하면, 다음과 같이 표현할 수 있다.

두 수열을 다음과 같이 정의한다. X = (x1,x2,...,xm), Y = (y1,y2,...,yn). X의 접두사는 X1,2,...m이고, Y의 접두사는 Y1,2,...n이다. LCS(X[i],Y[j])를 접두사 X[i]와 Y[j]의 최장 공통 부분수열을 대표한다고 둔다. 이 수열의 집합은 다음과 같이 주어진다.

X[i]와 Y[j]의 최장 공통 부분 수열을 찾기 위해서, 두 원소 xi와 yj를 비교한다. 만약 그들이 같다면 수열 LCS(X[i-1],Y[j-1])는 xi원소로 확장된다. 만약 그들이 같지 않다면 두 수열 LCS(X[i-1],Y[j])와 LCS(X[i][j-1])중 더 긴 것이 얻어진다. (만약 그 둘이 길이가 같지만 동일하지 않다면 둘다 얻어진다.) 이 공식들에서 첨자가 1씩 감소했음을 주목하라. 이것은 첨자가 0이 되는 상황을 만들 수 있다. 수열의 원소들은 1부터 시작하는 것으로 정의되어 있으므로, 첨자가 0일 때 LCS는 비어있다는 필요조건을 추가할 필요가 있다.

• 이제 정의의 조건들을 활용해서 문제를 풀어보자.

  1. string 타입으로 두 수열(a, b)을 입력받는다.
  2. 2중 for문을 활용해서 두 수열을 첫번째 원소부터 완전 탐색으로 비교한다. 비교하며 두 원소가 같을 경우 dp[i][j] = dp[i - 1][j - 1] + 1를 통해 이전까지의 dp값에 1을 더해주고, 다를 경우 dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])를 통해서 이전까지의 dp값에서 현재 비교하고 있는 문자를 각각 넣었을 때 더 긴 값으로 갱신해준다.
  3. 연산이 끝나면 dp[a.size()][b.size()]가 정답이다.

[코드]

//boj9251번_LCS_dp

#include<iostream>

int dp[1001][1001];

using namespace std;

int main() {
	string a, b;

	cin >> a;
	cin >> b;

	for (int i = 1; i <= a.size(); i++) {
		for (int j = 1; j <= b.size(); j++) {
			if (a[i - 1] == b[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}

	cout << dp[a.size()][b.size()];

	return 0;
}