게임 개발을 할 때 수학을 엄청 잘해야 하는 것은 아니라고 생각하지만 그래도 이 정도는 알아야 한다 싶은 기초 게임 수학에 대해 정리해 보려고 한다.

[1. 벡터]

<벡터란?>

크기와 방향을 동시에 가지는 수학적 개념.

• 게임에서는 오브젝트의 위치, 방향, 속도 등을 나타낼 때 벡터를 사용한다.
• Unity에서 Vector2는 2D, Vector3는 3D 공간에서 위치나 방향을 나타낼 때 사용된다.

벡터의 구성요소 위에 언급 한 내용과 같이 두가지가 존재한다.

• 크기 (Magnitude) : 벡터의 길이
• 방향 (Direction) : 벡터가 가리키는 방향

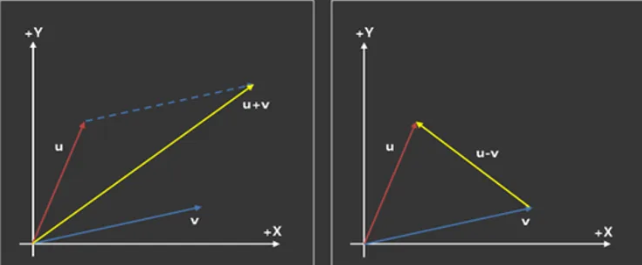
<벡터의 덧셈과 뺄셈>

• 벡터의 덧셈
  • 두 벡터를 더하여 새로운 벡터를 구함
  • 게임에서 두 지점 사이의 중앙 위치를 구할 때 사용
• 벡터의 뺄셈
  • 두 벡터를 빼서 거리와 방향을 구함
  • 적과 플레이어 사이의 상대적 위치 및 방향을 계산하는 데 주로 사용
• 벡터의 덧셈과 뺄셈 공식
  • 벡터 A : Vector3(x1,y1,z1)
  • 벡터 B : Vector3(x2,y2,z2)
    • 덧셈 : A+B = (x1+x2,y1+y2,z1+z2)
    • 뺄셈 : A-B = (x1-x2,y1-y2,z1-z2)

---

[2. 스칼라]

<스칼라란?>

방향이 없고 크기만을 가지는 물리량을 뜻하는 수학적 개념

<예시>

• 속력 : 오브젝트가 얼마나 빠르게 움직이는 지 나타내는 크기만의 값
• 체력 : 캐릭터가 가지고 있는 에너지를 나타내는 스칼라 값
• 거리 : 두 오브젝트 간의 떨어진 거리를 나타내는 스칼라 값

<벡터와의 관계>

벡터의 크기는 스칼라 값으로 표현되며, 스칼라 값을 벡터에 곱하면 벡터의 크기(길이)가 조절 된다.

• 벡터에 스칼라 곱하기
  • 벡터 A = Vector3(x,y,z)
  • 스칼라 B = s
    • 곱셈 : AB = (xs,ys,zs)

---

[3. 단위 벡터와 정규화]

<단위 벡터란?>

크기가 1인 벡터로, 방향만을 나타낸다.

• 벡터의 크기는 길이를 의미하며, 단위 벡터는 그 크기가 1로 고정되어 있다.
• 일반적으로 단위 벡터는 방향만을 표현할 때 사용된다.

<단위 벡터 구하는 법>

단위 벡터 = 벡터 / 벡터의 길이

Vector3 A = new Vector3(3, 4, 0);
float magnitude = A.magnitude;
Vector3 unitVector = A / magnitude;

<벡터 정규화 (Normalization)>

• 벡터 정규화
  • 주어진 벡터를 단위 벡터로 변환하는 과정.
  • 방향은 동일하지만 크기가 1인 벡터로 변환.
• 게임에서 벡터 정규화는 캐릭터나 오브젝트의 방향을 구할 때 자주 사용된다.
• 예를 들어, 적이 플레이어를 향해 이동할 때 정규화된 벡터를 사용하면 일정한 속도로 이동할 수 있다.

<단위 벡터의 사용 사례>

• 오브젝트 방향 제어

  • 오브젝트가 일정한 속도로 움직이도록 설정할 때, 정규화된 방향 벡터를 사용.
  • ex) 적이 플레이어를 향해 일정한 속도로 이동할 경우

• 카메라 이동

  • 카메라가 특정 방향을 바라보도록 설정할 때도 정규화된 방향 벡터를 사용

• 회전 계산

  • 단위 벡터는 회전 연산에서도 중요한 역할을 함

<정규화된 벡터의 장점>

• 일정한 속도 유지
  • 벡터를 정규화하면 속도에 관계없이 오브젝트가 일정한 방향으로 이동하게 된다.
  • 크기가 1이므로, 속도를 벡터에 직접 곱해서 일정한 속도로 움직일 수 있다.
• 정확한 방향 제어
  • 정규화된 벡터는 크기 대신 방향에만 집중하므로, 오브젝트의 이동 방향이나 회전 방향을 정확하게 제어할 수 있다.

---

[4. 벡터 내적 (Dot Product)]

<벡터 내적이란?>

두 벡터 사이의 각도와 관련된 값을 구하는 연산으로, 두 벡터가 얼마나 유사한 방향을 가리키는지 나타낸다. 수학적으로 내적은 두 벡터의 크기와 그 사이의 각도 θ에 따라 계산된다.

• 공식

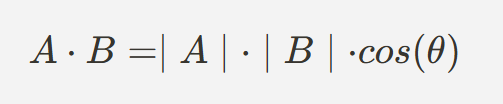
• 여기서 |A|와 |B|는 벡터 A와 B의 길이, θ는 두 벡터 사이의 각도이다.
• 내적의 결과는 스칼라 값(단일 숫자) 이다. 이 값은 두 벡터의 방향적 유사성을 나타내며, 두 벡터가 얼마나 같은 방향을 향하는지를 나타낸다.

<내적 값의 의미>

• 양수

  • 두 벡터가 서로 대체로 같은 방향을 가리키면, 내적 값은 양수이다.
  • A와 B의 내적이 1이면 두 벡터가 완전히 같은 방향을 가리키는 것이다.

• 0

  • 두 벡터가 직각이면, 내적이 0이다. 따라서 내적이 0이면 두 벡터가 서로 수직이라는 뜻이다.

• 음수

  • 두 벡터가 서로 대체로 반대 방향을 가리키면, 내적 값은 음수이다.
  • A와 B의 내적이 -1이면 두 벡터가 완전히 반대 방향을 가리키는 것이다.

<내적 계산 방법>

• 벡터 좌표로 내적 계산

• 두 벡터 A = Vector3(ax,ay,az), B = Vector3(bx,by,bz)가 있을 때, 내적은 다음과 같이 계산된다.

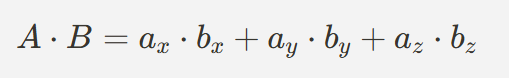
<두 벡터가 단위 벡터일 때 내적>

• 두 벡터가 모두 단위 벡터일 때, 내적 공식은 다음과 같이 단순화 된다.

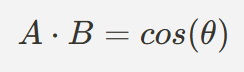
즉, 두 단위 벡터 간의 내적 값은 그 사이의 각도에 대한 코사인 값과 동일하다.

<내적을 이용한 두 벡터 사이의 각도 계산>

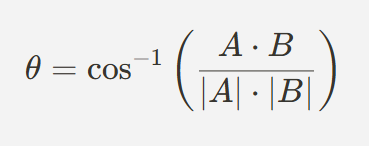
cos-1은 역코사인(arc consine)이며, 내적의 결과를 통해 각도를 계산하는 데 사용된다.

<하나의 벡터가 단위 벡터일 때 내적과 투영된 길이 계산>

• 내적을 통한 투영
  • 한 벡터가 단위 벡터일 때, 내적은 다른 벡터가 그 방향으로 얼마나 투영(Projection)되는지를 나타낸다.

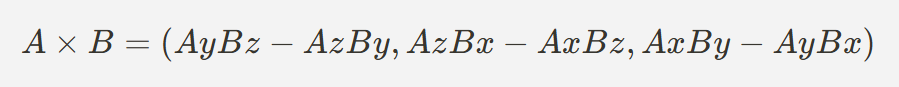
여기서 B^은 단위 벡터이다. 즉, 내적 값은 벡터 A가 단위 벡터 B 방향으로 투영된 길이를 나타낸다.

• 투영된 길이 계산

  • 한 벡터가 단위 벡터일 경우, 내적 값은 벡터 A의 크기와 단위 벡터 B의 방향에 대한 투영된 길이를 나타낸다.

  • 이 값은 물리적인 현상, 예를 들어 물체가 경사면을 따라 움직일 때 이동 거리 등을 계산하는 데 사용된다.

<투영된 길이의 해석>

투영된 길이는 벡터가 다른 방향으로 얼마나 투영되었는지를 나타내며, 실제로 해당 방향으로 이동하거나 힘을 가하는 상황에서 유용하다.

• 경사로 이동 : 캐릭터가 경사로를 오르거나 내려갈 때, 힘이 경사면의 방향으로 얼마나 투영되는지 계산하여 이동 속도를 제어

• 힘의 방향 계산 : 힘이 특정 방향으로 작용할 때, 그 힘이 얼마나 해당