[5. 벡터 외적 (Cross Product)]
<벡터 외적(Cross Product)>
두 벡터 사이의 직각(수직) 방향 벡터를 계산하는 연산.
- 두 벡터가 평면을 이루면, 외적은 그 평면에 수직인 새로운 벡터를 생성한다.
- 수학적으로, 두 벡터 A와 B의 외적은 다음과 같이 계산된다.
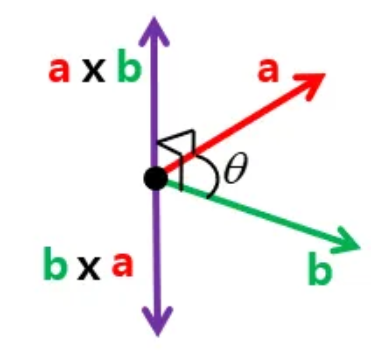
- 외적의 특징
- 외적의 결과는 벡터이다. 즉, 외적의 결과는 크기와 방향을 가지는 새로운 벡터이다.
- 외적 벡터의 방향은 오른손 법칙에 의해 결정된다.
- 벡터 A에서 벡터 B로 회전할 때, 오른손의 엄지를 제외한 네 손가락이 회전하는 방향을 가리키고, 엄지가 수직 벡터의 방향을 나타낸다.
하지만 우리는 유니티는 왼손 좌표계를 사용하기 때문에 우리는 왼손 법칙을 이용해야한다.
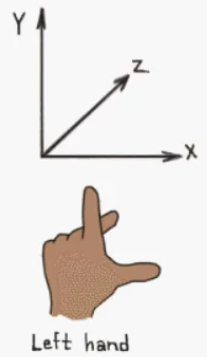
<외적의 결과>
- 크기
- 외적 결과의 크기는 두 벡터 사이의 평면의 넓이와 관련이 있다.
- 두 벡터가 이루는 평행사변형의 넓이로 해석할 수 있으며, 크기는 다음과 같이 계산된다.

- θ는 두 벡터 사이의 각도. 외적의 크기가 크다는 것은 두 벡터가 서로 수직에 가까워질수록 더 넓은 평행사변형을 이루는 것을 의미한다.
- ex) 두 벡터가 평행하면 θ=0 이므로 외적의 결과는 0이다.
- 방향
- 외적 결과 벡터의 방향은 두 벡터가 이루는 평면에 수직이다.
- 이 수직 벡터는 물지럭 회전 방향이나 3D 그래픽에서의 법선 벡터를 계산할 때 사용된다.

- 이 수직 벡터는 물지럭 회전 방향이나 3D 그래픽에서의 법선 벡터를 계산할 때 사용된다.
- 외적 결과 벡터의 방향은 두 벡터가 이루는 평면에 수직이다.
<외적과 내적의 차이>
-
외적은 두 벡터가 이루는 평면에 수직인 벡터를 반환하며, 이 벡터의 크기는 두 벡터 사이의 각도와 관계있다. 방향을 나타낼 때 사용된다. -
내적은 두 벡터 사이의 각도나 유사성을 계산하는 데 사용된다. 내적 값은 두 벡터가 얼마나 같은 방향을 가리키고 있는지 나타낸다.
<벡터 외적의 활용 사례>
- 회전 방향 계산 : 외적을 사용하여 회전의 방향을 계산할 수 있다.
- ex) 비행기의 방향을 결정하거나, 포탑이 적을 향할 때 회전 방향을 결정하기 위해 사용
- 법선 벡터 계산 : 면의 법선을 계산하여 충돌이나 물리 연산에서 면이 가리키는 방향을 구할 수 있다.
- ex) 3D 그래픽에서 조명 계산 시, 외적을 통해 면의 법선 벡터를 구해 빛의 반사 방향을 결정.
[6. 행렬 연산과 변환]
<행렬의 기본 개념>
- 행렬(Matrix)은 수학적으로 숫자를 배열한 2차원 구조로, 수학적 연산을 통해 데이터를 다룬다. 게임 프로그래밍에서는 주로 오브젝트의 변환(Transformation), 즉 이동(Translation), 회전(Rotation), 크기 변환(Scale)을 처리할 때 사용된다.
- 행렬의 차원
- 행렬은 행과 열로 구성되며, 2x2, 3x3, 4x4 같은 형태로 표현된다.
- 2x2 행렬과 3x3 행렬은 2D와 3D 공간에서 오브젝트의 변환을 처리할 때 사용할 수 있지만, 3D 게임에서는 주로 4x4 행렬을 사용한다. 이 행렬은 위치, 회전, 크기 변환을 동시에 처리할 수 있다.
- 4x4 변환 행렬의 구조
- 4x4 행렬은 다음과 같은 구조를 가진다.
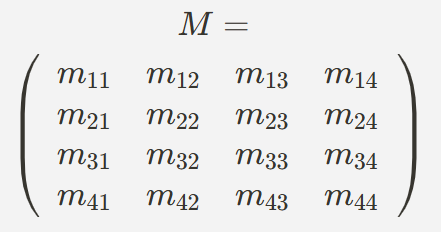
- 3D 오브젝트의 변환을 위한 중요한 요소는 이 행렬의 마지막 열에 위치한다. 이 열은 오브젝트의 위치(이동), 크기 변환, 회전을 나타낸다.
- 4x4 행렬은 다음과 같은 구조를 가진다.
<행렬 덧셈과 곱셈>
-
행렬 덧셈(Matrix Addition)
- 행렬 덧셈은 같은 크기의 행렬에서 각 성분을 더하는 방식으로, 두 행렬이 같은 차원(크기)일 때만 가능하다.
- 예를 들어, 두 2x2 행렬 A와 B가 주어졌을 때
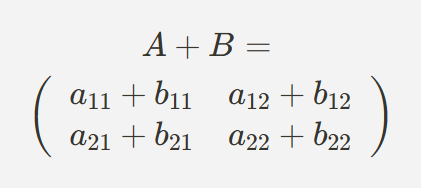
- 이는 각 요소가 서로 대응되는 위치에서 더해진다.
-
행렬 곱셈(Matrix Multiplication)
- 행렬 곱셈은 더 복잡한 연산으로, 두 행렬이 곱해질 때 각 성분의 합을 구하여 새로운 행렬을 만든다.
- 두 행렬 A와 B의 곱셈
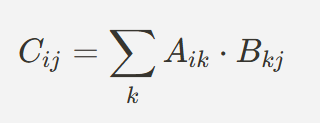
- 예를 들어, 두 2x2 행렬 A와 B를 곱할 때
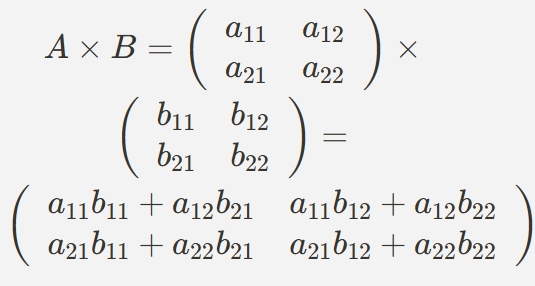
-
행렬 곱셈의 활용
- 행렬 곱셈은 여러 변환(이동, 회전, 크기 변환)을 결합할 때 사용된다. 예를 들어, 오브젝트가 이동한 후 회전하고, 크기를 변경하려면 각 변환을 차례대로 적용한 후 하나의 변환 행렬로 결합해야 한다.

- 행렬 곱셈은 여러 변환(이동, 회전, 크기 변환)을 결합할 때 사용된다. 예를 들어, 오브젝트가 이동한 후 회전하고, 크기를 변경하려면 각 변환을 차례대로 적용한 후 하나의 변환 행렬로 결합해야 한다.
-
여기서 M은 최종 변환 행렬, T는 이동 행렬, R은 회전 행렬, S는 크기 변환 행렬이다.
<TRS(Translation, Rotation, Scale) 변환>
-
TRS 변환이란, 오브젝트의 이동(Tranlation), 회전(Rotation), 크기 변환(Scale)을 하나의 변환 행렬로 결합하여 처리하는 방식이다. -
이동 (Translation) 행렬
- 이동 행렬은 오브젝트를 특정 좌표로 이동시키는 변환을 처리한다.
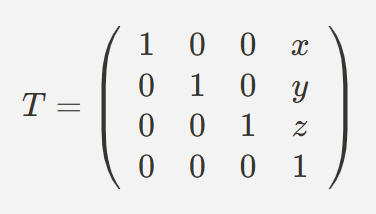
- 여기서 x,y,z는 오브젝트가 이동할 좌표이다.
- 이동 행렬은 오브젝트를 특정 좌표로 이동시키는 변환을 처리한다.
-
회전(Rotation) 행렬
- 회전 행렬은 X,Y,Z축을 기준으로 오브젝트를 회전시키는 변환을 처리한다.
- X축 회전
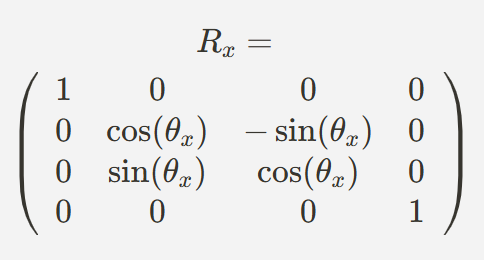
- Y축 회전
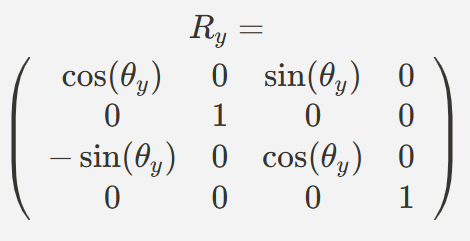
- Z축 회전
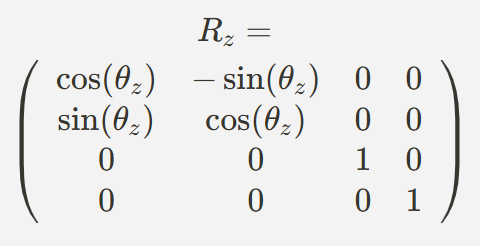
- X축 회전
- 회전 행렬은 X,Y,Z축을 기준으로 오브젝트를 회전시키는 변환을 처리한다.
-
크기 변환(Scale) 행렬
-
크기 변환 행렬은 오브젝트의 크기를 조정하는 변환 처리를 한다.
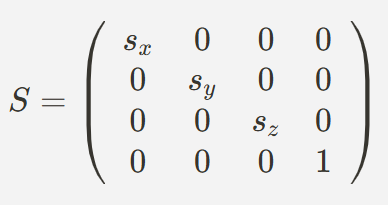
-
여기서 sx,sy,sz는 각각 X,Y,Z축에 대한 크기 변환 값을 나타낸다.
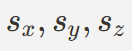
-
TRS 변환의 결합
- TRS 변환은 이동, 회전, 크기 변환을 각각의 행렬로 계산한 후 이들을 곱하여 하나의 변환 행렬로 결합하는 것이다.

- 이 결합된 행렬 M을 사용해 오브젝트의 변환을 적용할 수 있다.
- TRS 변환은 이동, 회전, 크기 변환을 각각의 행렬로 계산한 후 이들을 곱하여 하나의 변환 행렬로 결합하는 것이다.
-
TRS 메서드를 이용한 변환 계산
- Unity에서 Matrix4x4.TRS() 메서드를 사용하면 이동, 회전, 크기 변환을 하나의 메서드로 결합할 수 있다.
Matrix4x4 trsMatrix = Matrix4x4.TRS(new Vector3(5,0,0), Quaternion.Euler(0,90,0), new Vector3 (2,2,2));
<행렬과 벡터를 이용한 회전>
-
행렬-벡터 곱셈은 3D 그래픽스에서 회전, 이동, 크기 변환 등을 포함한 모든 변환을 다루는 방법이다.
-
3x3 회전 행렬을 사용하여 벡터를 회전시키는 방식이다.
-
행렬 변환은 모든 변환(이동, 크기, 회전)을 하나의 행렬로 결합할 수 있는 장점이 있다.
3D 공간에서 회전을 표현하는 3x3 행렬은 다음과 같은 형태이다. 예를 들어, Z축을 기준으로 회전하는 회전 행렬은 다음과 같다.
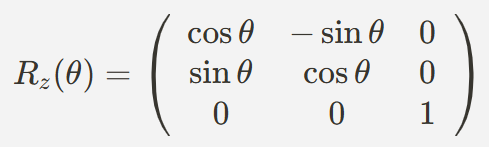
이 행렬을 벡터 V=(vx,vy,vz)에 곱하여 회전시킨다.
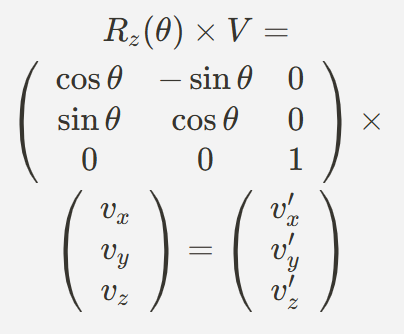
<쿼터니언과 벡터를 이용한 회전>
- 쿼터니언은 회전 변환을 나타내는 4차원 복소수로, 주로 3D 회전에 특화되어 있다.
- 쿼터니언을 이용하면 벡터를 회전시킬 수 있다.
- 여러 번의 회전이 필요할 때 부드럽고 안정적인 회전을 제공하며, 특히 짐벌락(Gimbal Lock) 문제를 방지할 수 있는 장점이 있다.
쿼터니언 q = w+xi+yj+zk는 회전 축과 회전 각도를 포함한다. 벡터 V=(vx,vy,vz)를 쿼터니언으로 회전시키려면, 다음과 같은 과정을 거친다.
- 벡터를 쿼터니언 형식으로 확장
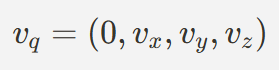
- 쿼터니언 곱셈을 통해 회전
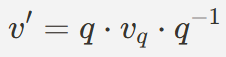
- 여기서 q-1은 쿼터니언의 역원이다.
<Unity에서의 쿼터니언과 벡터를 이용한 회전>
-
Unity는 쿼터니언을 사용하여 3D 회전을 매우 쉽게 처리할 수 있도록 설계되어 있다.
-
Unity에서 벡터를 회전할 때, Quaternion * Vector3 연산자를 통해 쿼터니언과 벡터의 곱셈을 간편하게 사용할 수 있다.
-
쿼터니언의 곱셈은 비가환적이다. 즉, 두 쿼터니언을 곱할 때 순서가 매우 중요하다.
-
Unity에서 쿼터니언과 벡터 곱셈
Unity에서 쿼터니언을 사용해 벡터를 회전시키는 기본적인 방식은 다음과 같다.
using UnityEngine; public class QuaternionRotation : MonoBehaviour { void Start() { // Y축을 기준으로 90도 회전하는 쿼터니언 Quaternion rotation = Quaternion.AngleAxis(90, Vector3.up); // 회전할 벡터 (X축 방향) Vector3 vector = new Vector3(1, 0, 0); // 벡터를 회전시킴 Vector3 rotatedVector = rotation * vector; // 결과 출력 Debug.Log("회전된 벡터: " + rotatedVector); } }
[7. 아크 탄젠트와 방향 계산]
<아크 탄젠트란?>
- 아크 탄젠트는 삼각함수의 역함수로, 주어진 x/y 값으로 각도를 반환
- 주요 목적
- 각도를 라디안(rad) 단위로 계산
- 좌표계 상에서 두 점 간의 방향을 찾음
- 유니티에서는 Mathf.Atan2를 주로 사용
<유니티에서의 아크 탄젠트 함수>
- Mathf.Atan(float value)
- 입력값 : value(float)
- ex) 특정 기울기의 각도 구하기
- Mathf.Atan2(float y, float x)
- 입력값 : y(세로 방향), x(가로 방향)
- ex) 두 점 간의 방향(벡터의 각도) 계산
<플레이어가 적을 바라보는 방향 구현하기>
- 플레이어가 적 방향으로 회전하도록 설정
- 두 점(프렐이어 위치와 적 위치) 사이의 방향 각도를 계산
using UnityEngine; public class PlayerLookAt : MonoBehaviour { public Transform enemy; // 적의 Transform void Update() { // 1. 플레이어와 적 간의 위치 차이 계산 Vector3 direction = enemy.position - transform.position; // 2. 방향 벡터를 통해 각도 계산 float angle = Mathf.Atan2(direction.y, direction.x) * Mathf.Rad2Deg; // 3. 플레이어 회전 설정 transform.rotation = Quaternion.Euler(new Vector3(0, 0, angle)); } }
<주의점 및 팁>
- 좌표계 변환
- Unity에서 Mathf.Atan2의 결과는 라디안 단위이므로, Mathf.Rad2Deg를 곱해서 각도로 변환
- 3D와 2D의 차이
- 2D 게임에서는 x/y 좌표로 계산
- 3D 게임에서는 y축(수직 회전) 또는 z축을 고려 해야함

