[백준] 11726번: 2xn 타일링

💻 문제 - S3

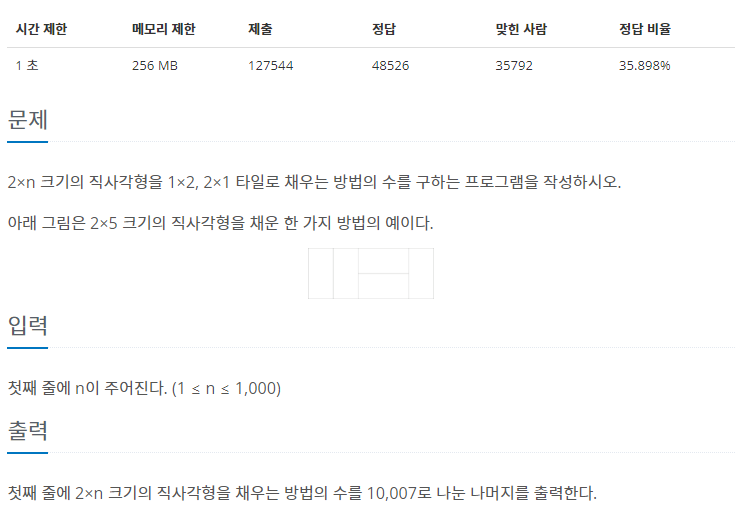
n이 1일 때와 2일 때 각각 1가지와 2가지 경우의 수가 있다는 사실을 알기 때문에 bottom-up 방식으로 접근한다. n을 증가시키면서 방법의 수를 조금만 계산해보아도 다음과 같은 점화식을 얻을 수 있었다.

dp[i] = dp[i-1] + dp[i-2]

👉 제출 코드

n = int(input())
dp = [0] * (n+1)
dp[1] = 1
dp[2] = 2
for i in range(3, n+1):
    dp[i] = dp[i-1] + dp[i-2]
print(dp[n]%10007)

런타임 에러 발생하여 dp 배열 부분을 수정하였다.

n = int(input())
dp = [0, 1, 2]
for i in range(3, n+1):
    dp.append(dp[i-1] + dp[i-2])
print(dp[n]%10007)

🙏 다른 사람의 풀이 보기

dp = [0, 1, 2]
for i in range(3, 1001):
  dp.append(dp[i - 2] + dp[i - 1])
n = int(input())
print(dp[n] % 10007)

• n의 개수가 1000보다 작다는 조건이 있으므로 for문을 1000까지 연산한다.
• 1000보다 n+1이 더 효율적인 경우가 있다고 생각한다.