Curve 25519ㅡ 임시
1. introduction
본 논문에서는 다양한 암호화 응용에 적합한 타원곡선 Diffie-Hellman 함수인 Curve 25519를 소개 및 분석. 높은 보안 및 빠른 속도를 위해 Cureve 25519 사용.
Curve25519의 High-level view는 다음과 같음.
각 Curve 25519 사용자는 32byte 비밀키 및 공개키를 가짐. 두 Curve 25519 사용자의 각세트에는 두 사용자 간의 통신?에는 32바이트 비밀키로 암호화된 메시지를 이용.
Midium lebel view는 다음과 같음
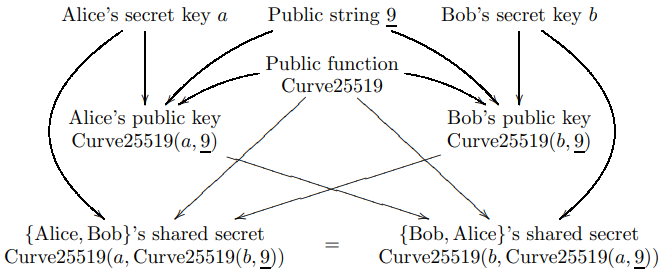
공유 비밀(메시지를 의미) Curve25519(a, Curve25519(b, 9))의 해시는 비밀 키 인증 시스템의 키로(메시지를 인증하기 위해) 또는 비밀 키 인증된 암호화 시스템을 위한 키로 사용(암호화 및 인증에 이용).
Low-Level view: Curve25519함수는 에 대한 의 x좌표 스칼라곱. 여기서 p는 소수 E는 타원 곡선 .
추측되는 보안 수준
Curve25519 함수 해킹하기 - 예를 들어,두 개의 공개 키에서 공유 비밀을 계산하는 것은 매우 어려운 것으로 추측됩니다. 알려진 모든 공격은 일반적인 128비트 비밀 키 암호에서 무차별 대입 검색을 수행하는 것보다 비용이 많이 듭니다.
타원 곡선 이산 로그의 일반적인 문제는 거의 성공하지 못한 채 20년 동안 공격을 받아 왔습니다. 일반 이산 대수 알고리즘은 충분히 크지 않은 소수 그룹을 끊지만, 이 논문에서 사용된 소수 그룹의 크기는 2252 이상입니다. 특정 특수 대수 구조를 가진 타원 곡선은 일반 알고리즘이 아닌 알고리즘을 사용하여 훨씬 더 빨리 깨뜨릴 수 있지만 에는 이러한 구조가 없습니다.
대형 양자 컴퓨터가 구축되면 Curve25519 및 기타 모든 단축 키 이산 로그 시스템이 중단됩니다. 일반 타원 곡선 이산 로그 알고리즘에 대한 자세한 내용은 [56]을 참조하십시오. 이 관찰의 결과
이 문서의 주제와 직교하며 더 이상 논의되지 않습니다.
효율성
- 빠른속도
- 시간에 따라 변화하지않음
- 짧은 비밀키
- 짧은 공개키
- 무료 키 검증
- 짧은 코드
Curve25519의 설계 및 구현에서 전역적으로 최적화하려고 시도했습니다.
• 특성 2가 아닌 큰 특성을 사용
• 곡선 모양 y2 = x3 + Ax2 + x를 사용
• (x, y)가 아닌 x를 공개 키로 사용
• 키가 꼬이는 것을 방지 하기위해 안전한 곡선 이용
• 또는 가 아닌 스칼라 곱셈 내부에서 를 사용합니다.
• 가변 배열 인덱싱을 산술로 변환합니다.
• 비밀 키의 선행 1에 대해 고정된 위치를 사용합니다.
• 비밀 키에 2의 작은 거듭제곱을 곱하여 곡선 그룹과 트위스트 그룹의 보조 인자를 설명합니다.
• 확장 필드가 아닌 프라임 필드를 사용합니다.
• 일부 b에는 2b에 매우 가까운 소수를 사용합니다.
• b/w가 정수가 아니더라도 일부 w에 대해 기수 2b/w를 사용합니다.
• 가능한 한 빨리 각 계수를 줄이는 대신 기수보다 약간 큰 계수를 허용합니다.
• 계수를 정수 레지스터가 아닌 부동 소수점 레지스터에 넣습니다. 그에 따라 w를 선택하십시오.
2. Specification
이 섹션에서는 Curve25519 함수를 정의합니다. ring, field, elliptic curve 익숙하지 않은 독자는 정리 2.1의 정의와 증명에 대해 부록 A를 참조해야 합니다.
타원 곡선에 대한 자세한 내용은 [24, 13장]을 참조하십시오.<--CLOSED
BASE FILED
p를 5이상의 소수라고 하자. 로 정의.
에서 이진 연산 +를 addition mod P로 정의
에서 이진 연산 를 multiplication mod P로 정의.
단항연산에서 -는 부정의 의미로 정의
는 0,1,-,+,* 교환 가능.
즉 항등식 a(b+c+1) = ab + ac + a.
p가 소수이기 때문에 는 필드. 영이 아닌 요소는 역수를 가짐.

