ED 25519(1)

솔라나에서 사용하는 암호화 키 방식인 ED 25519에 대해 공부해보고자 한다.

ed25519(이하 ECC)는 흔히 github 계정 설정할때 많이 접하게 되며, 우리는 ssh-keygen 옵션을 rsa와 ed-25519중에 선택해서 사용하게된다.

rsa/ECC는 다양한 암호화 알고리즘 분야 중 디지털 서명 알고리즘(DSA ; Digital Signature Algorithm)의 종류이다.

ECC는 SHA-152 및 curve 25519를 사용한 EDDSA 서명 체계이다.

Abstract

ECC 논문의 초록에는 다음과 같은 내용이 요약되어 있다.

당시 $390 가격인 대중적인 CPU(Xeon E5620) 으로 109000개의 서명이 생성가능.
$2^{128}$의 보안 수준을 가지며 초당 71,000개 서명을 확인.
Public key는 32바이트, 서명은 64바이트. 강력한 공격 방어 기능.
비밀키는 어레이 인덱스로 데이터 흐름이 없고, 분기조건으로 데이터 흐름이 없음

데이터 흐름이 무엇을 의미하는지는 더 읽어 봐야 알 것 같다.

1. Introduction

인트로 덕션에는 ED 방법의 장점에 대해 나열되어있다.

• Fast single-signature verification(빠른 단일-서명 확인)
  2008~2010년 사이에 출시된 Intel cpu 기준 서명에 273364 사이클만 소요.
• Even faster batch verification(더 빠른 일괄 검증)
  855만 사이클에서 64개의 개별 서명 확인. 즉 단일 서명 기준 13.4만 사이클 소요
  시간으로 환산시 2.4GHZ cpu 기준 최대 검증시간 4밀리초 미만, 초당 7.1만개 서명 검증
• Very fast signing(매우 빠른 서명)
  메시지에 서명하는데 8.7만 사이클 소요. 쿼드쿼어 2.4Ghz cpu 기준 초당 10.9만개 메시지 서명
• Fast key generation(빠른 키 생성)
  키 생성은 서명 만큼 빠름. 운영체제에서 안전한 난수 생성을 위해 약간의 패널티 사용. Linux /dev/urandom의 코스트는 6000 사이클
• High security level(높은 보안 레벨)
  $2^{128}$ 보안 목표. 3000비트 RSA와 비슷한 수준의 어려움. 이를 공격하려면 평균 2140비트 이상의 연산 수행이 필요.
• Foolproof session keys(완벽한 세션 키)
  모든 서명은 결정적 생성. 키 생성은 random을 이용하지만 서명은 아님. 이것은 속도 뿐만아니라 보안과도 직결됨.
• Collision resilience(충돌 복원력)
  해쉬 함수 충돌은 시스템을 손상 시키지 않음.선택된 해시함수의 약점 가능성에 대한 방어 기능
• No secret array indices(비밀 배열 인덱스가 없음)
  램의 비밀 주소에서 읽거나 쓰지 않음. 주소 패턴은 완전히 예측 가능함. 따라서 캐시 타이밍 공격, 하이퍼 스레딩 공격 및 주소 누출에 의존하는 기타 공격에 면역 기능
• No secret branch conditions( 비밀 분기 조건이 없음)
  비밀 데이터를 기반으로 조건부 분기를 수행하지 않음.점프패턴(?) 은 수전 가능. 따라서 분기 예측 장치를 통한 정보 누출에 의존하는 부채널 공격 면역.
• Small signature(작은 서명)
  서명은 64바이트 이용.압축 및 압축해제는 위에서 얘기한 사이클에 포함됨
• Small key(작은 키)
  공개키는 32바이트만 사용.압축 및 압축해제는 위에서 얘기한 사이클에 포함됨

서명 기법은 타원 곡선을 이용하였음.
세션 2는 서명 시스템 설명, 세선3은 유한 필드 산술에 대한 설명. 세션4는 빠른 서명에 대한 설명. 세션 5는 검증에 대한 설명.

이전 타원 곡선과 비교

단일 CPU를 이용한 타원 곡선 서명 검증을 한 사례는 없음.
ECC성능 결과를 비교하는데 어려움이 있음
1. 빠른 ECC에 대한 논문은 ECDH(가변 기준점 단일 스칼라 곱셈)으로 제한. 서명검증은 구현 않음

• 예외사례 두가지가 있으며 ECDH보다 1.33배 1.36배 느린 검증 보고.(21,34 ref)

2. 대부분의 구현은 비밀 배열 인덱스와 분기조건을 사용함으로 부채널 공격에 대해 손상가능. 이것은 ECDH의 문제
3. 대부분의 논문은 소수의 CPU에 대한 결과만 보고. eBATS 밴치마크 시스템에서 그에 대한 문제 보고

본 논문이전에 본논문과 가상 유사한 방법은 ecdonaldp256:NIST P-256 ECC 기법.
이 방법은 키 생성에 169만 사이클, 서명에 179만 사이클. 검증에 208.7만 사이클. ECDH보다 높은 속도 보고

ECDH 구현 밴치마크 등수는
1등 gls1271 with endmorphism - 27.8만 사이클
2등 ecff256e simillar to curve 25519- 30.7만 사이클
3등 curve25519

최근 논문들은 endmorphism에 대한 문제 지적. 일부 ECC 프로토콜에선 ECDH 출력의 해싱을 사용하는 ECDH와 관련이 없고, ECC 서명과 상관 없음을 알 수 있음

이전 서명 시스템과 비교

eBATS 밴치마크는 RSA,DSA,ECDSA등 42개의 서명 시스템과 비교.
기존의 통념은 RSA가 ECC보다 훨씬 빠르기 대문에 여러번 검증하는 애플리케이션에서 RSA가 더 좋다고 생각함.
우리의 ECC속도 결과는 이에 의문을 제기함.
검증속도가 동일한 보안 수준에서 RSA를 능가할 수 없다고 주장하진 않지만, 검증 집약적인 어플리케이션에서도 ECC를 매력적인 옵션으로 둘만큼 빠르다고 주장.

2. 서명 시스템

이 문서에서 사용된 서명 시스템과 다른 타원 곡선과 함께 이용할 수 있는 일반화 된 서명 시스템 EdDSA를 지정. EdDSA는 DSA와 ECDSA의 변형 중 하나. 새로운 서명 시스템을 주장하지 않지만 최상의 성능 위해 조합을 잘 선택하는것이 중요하다는 것을 강조. Weierstrass 곡선 보다 twisted Edwards curve를 이용하는 것이 키 아이디어.

EdDSA 파라미터

EdDSA에는 7개의 파라미터가 있음.
$b$ : 정수 $b≥10$
$H$ : 암호화 해시함수 $H$. $2b$ 비트 출력
$q$ : $1 mod 4$ 에 합동인 소수의 거듭제곱 $q$
$F_q$ : $(b-1)bit$ 인코딩 요소를 가지는 필드
$d$ : $F_q$의 제곱이 아닌 요소
$l$ : 아래의 추가 제약을 충족하는 $2^{2b-4}$ 와 $2^{2b-3}$을 만족하는 소수
$E$ : 에드워드 타원 곡선

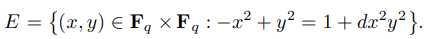
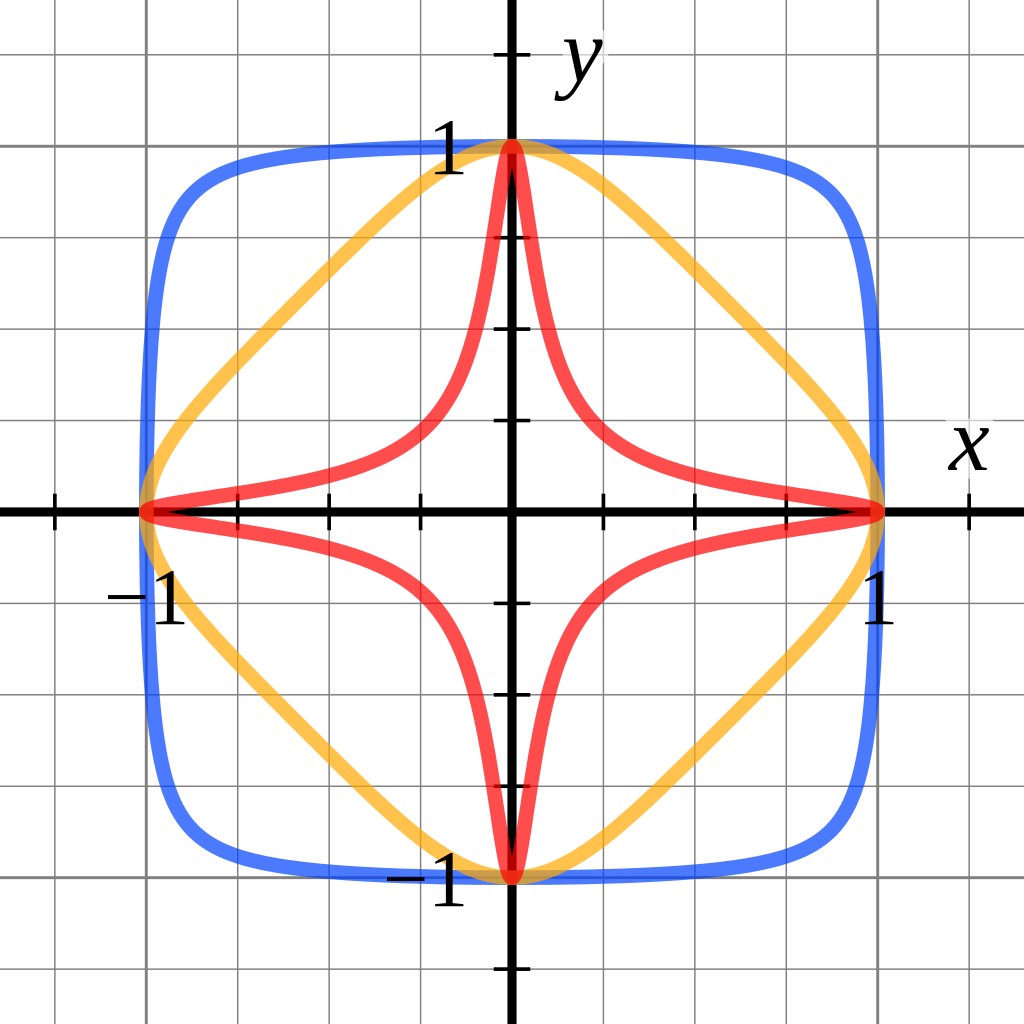
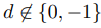
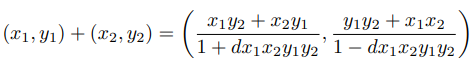
twisted Edward 법칙은 [13]에서 소개됨. 덧셈 법칙은 위 식에서 분모가 0이 아니라는 전제하에 제대로 동작함. -1은 $F_q$의 제곱(q가 1mod4의 합동임으로).

EdDSA 키 그리고 서명

EdDSA 비밀키는 b비트 문자열 k. 그만큼 해시 $H(k) = (h_0,h_1,....h_{2b-1})$의 정수를 결정

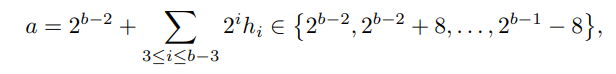
이는 차례로 A = aB를 결정. 해당 EdDSA 공개키는 A. 비트 ${h_b...,h_{2b-1}}$는 서명의 일부로 사용.

비밀키(k) 서명을 통한 메시지는 다음과 같이 정의

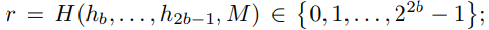
• 내용이 어려워 더 공부 후 작성 예정