Elliptic Curve

최완식·2023년 1월 11일

Bitcoin Cryptography Linear Transformation blockchain linear secp256k1

Bitcoin Programming

목록 보기

2/8

암호학에서 중요하게 사용되는 타원곡선에 대해 알아보자. 왜 해당 곡선을 사용할까?

타원곡선

y^2 = x^3 + Ax + B

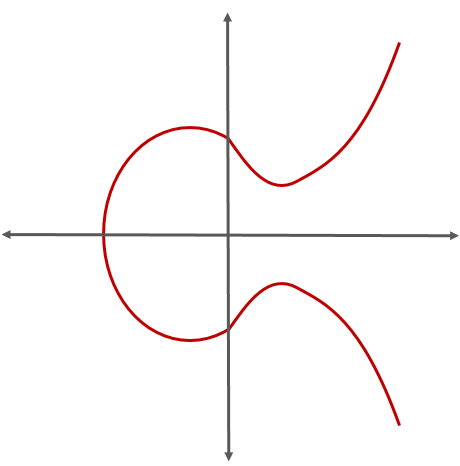
위의 방정식의 형태로 나타나는 곡선
타원의 둘레를 구하기 위한 적분, 이의 역함수를 구하는 과정에서 유래했다.
- 그렇기 때문에 곡선 형태만 봐서는 타원과 연관이 있는지 모르겠다.
실해석학, 복소해석학, 대수기하학, 정수론 모두에서 이야기되는 중요한 대상이다.
엄밀히 말하면 첨점, 교차점과 같은 특이점이 없는 형태여야 한다.
- $A$ , $B$ 는 동시에 0이어서는 안된다.
- 그렇게 될 경우 (0, 0)에서 특이점을 갖게된다.
자세한 내용은 위키를 참고하자.

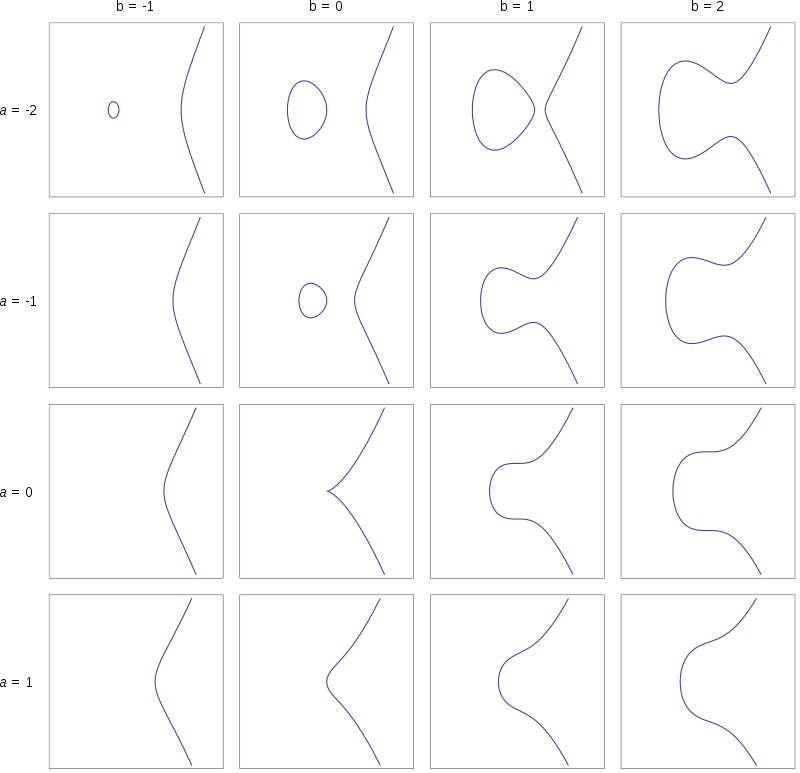
계수에 따라 다양한 모양이 가능하다.

secp256k1

y^2 = x^3 + 7

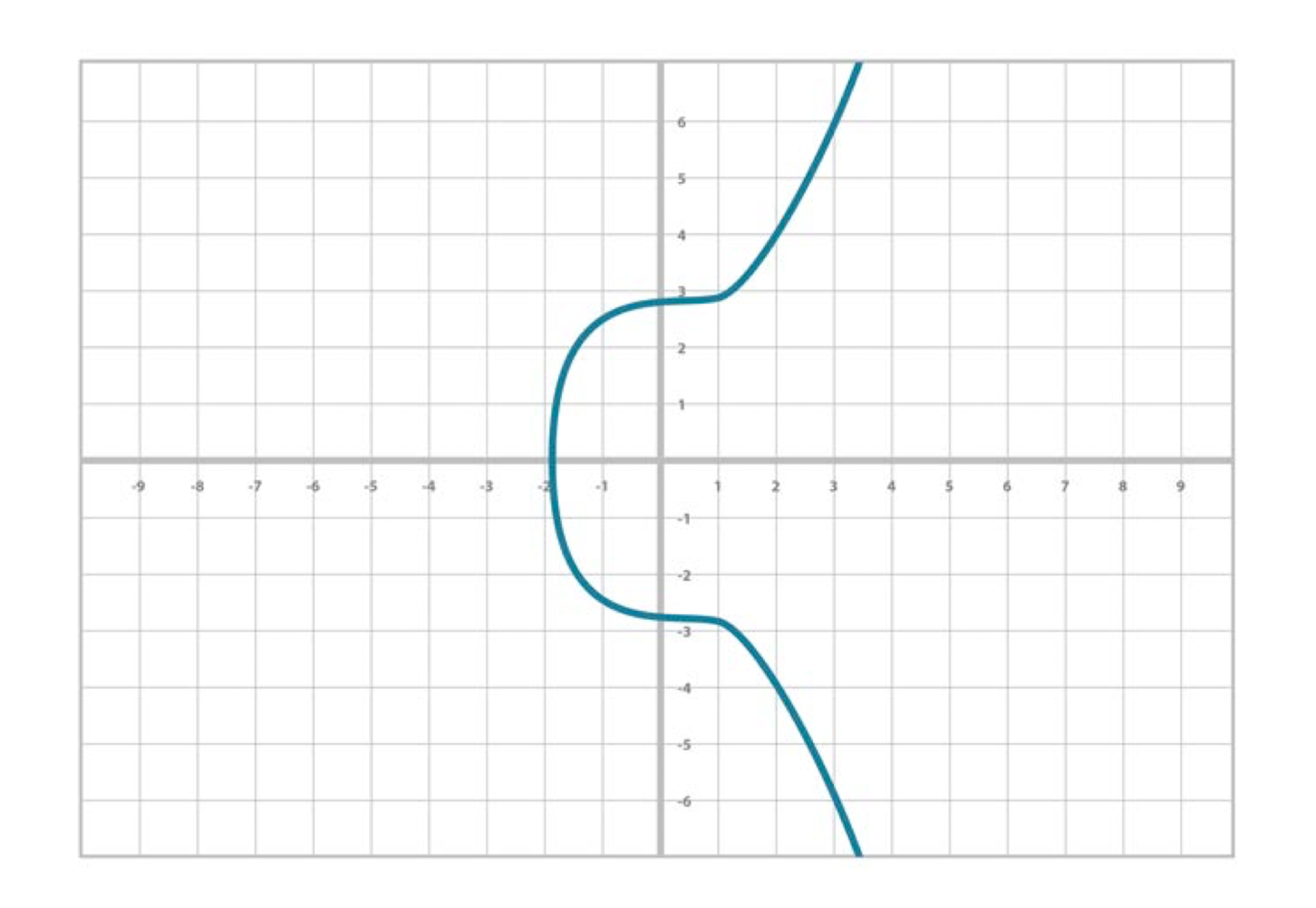
비트코인에서 사용되는 타원 곡선의 이름이다.

타원 곡선에서 그은 직선의 종류

비트코인에서 사용하는 특정 타원 곡선은 나중에 알아보자.
그 대신, 일반적인 타원 곡선에서 직선을 그었을 때,
나올 수 있는 패턴들에 대해 알아보자.

일반적인 경우
한 점에서 만남	세 점에서 만남

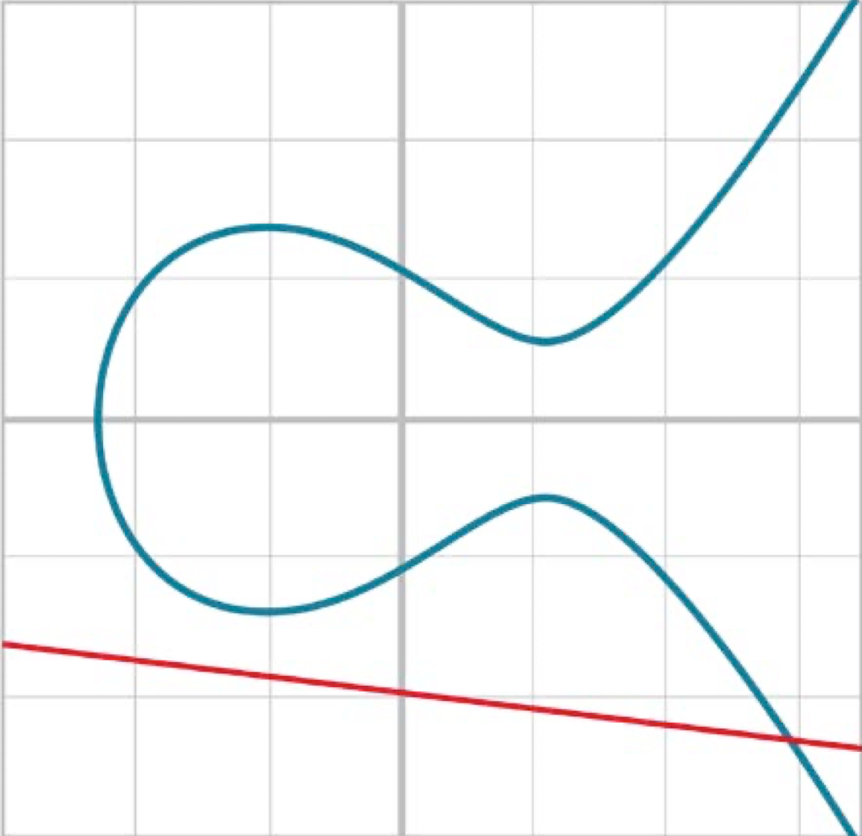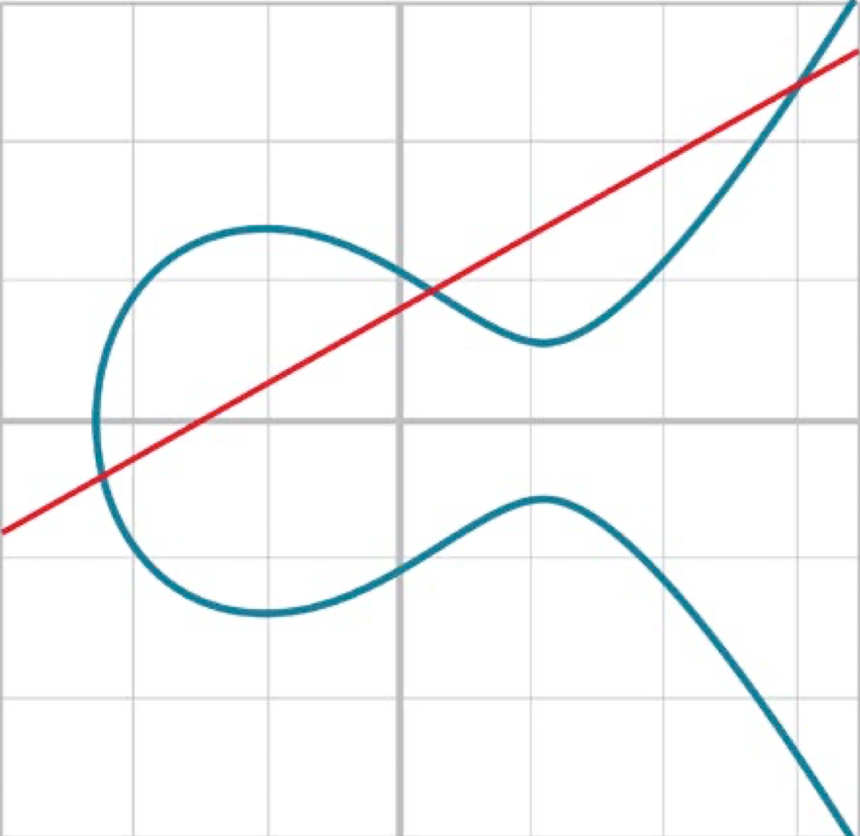예외 사항
두 점에서 만남(y축과 평행)	두 점에서 만남(접선)

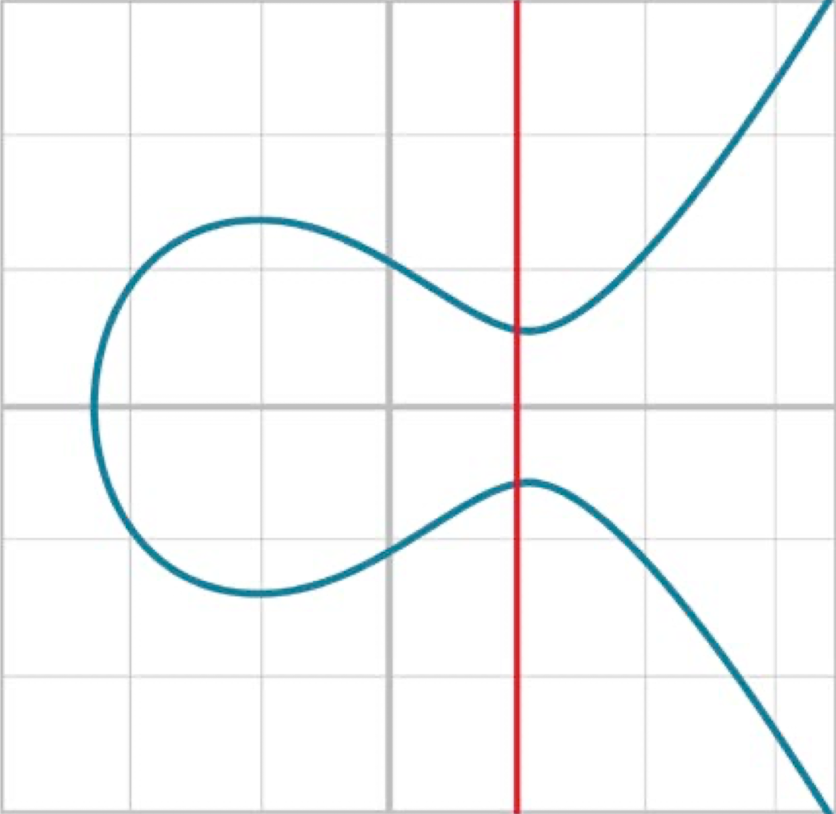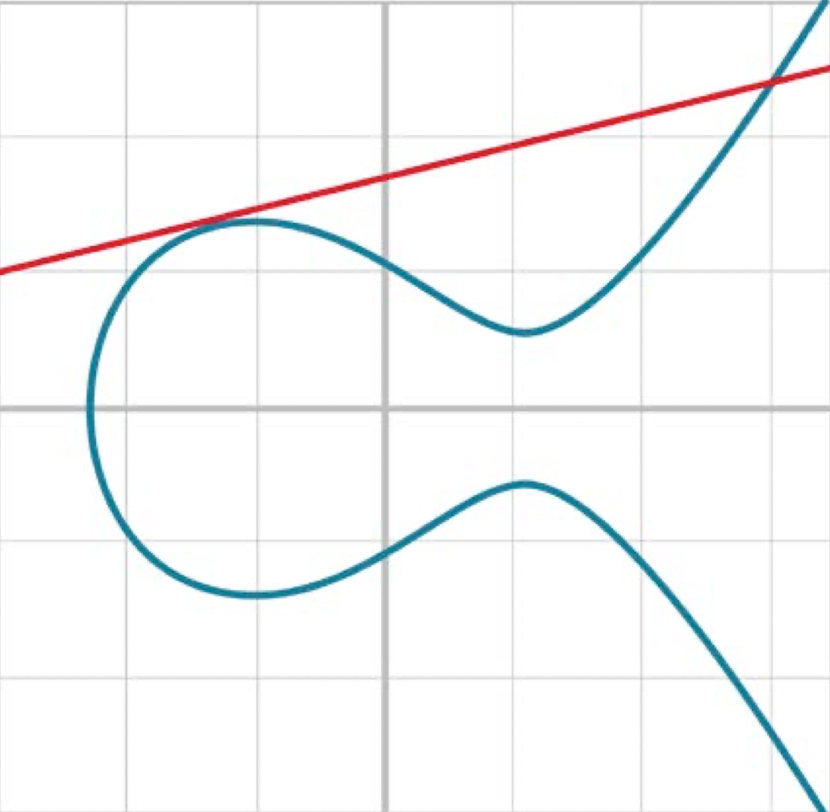타원 곡선 위의 두 점 덧셈

Note: 컴퓨터에서 실제로 사용하는 것은, 특정 곡선위에 있는 점의 성질이다.
그렇기 때문에 위의 타원 곡선위에 있는 점자체를 표현할 수 있도록만 처리할 예정이다.

타원 곡선위에 있는 점들에 관해 덧셈 연산을 정의해보자.

정의

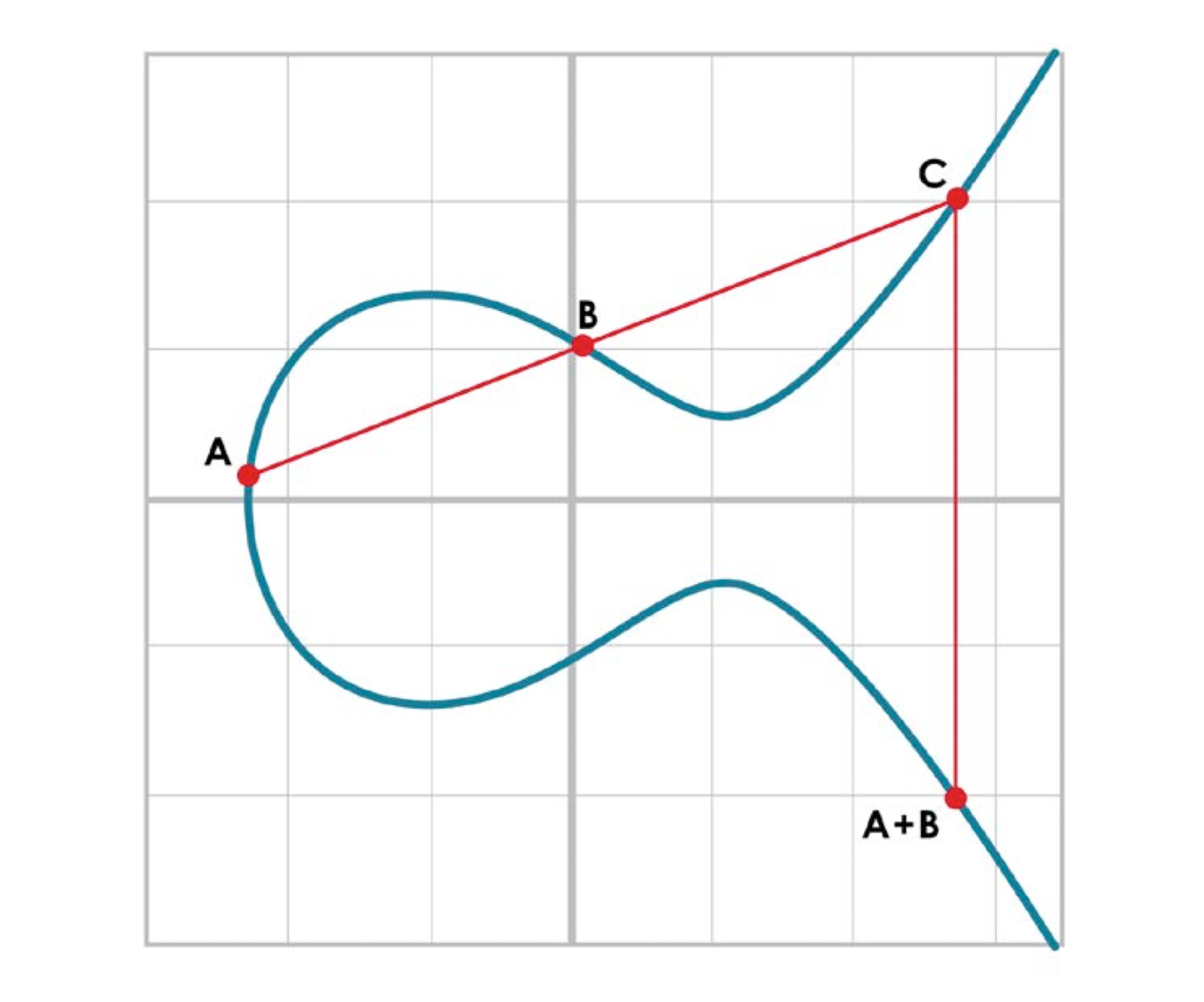
A+B = x축 대칭(A와 B를 지나는 직선이 만나는 세번째 교점)

세 점에서 만나는 경우에서 위와 같이 연산을 정의한다.
따라서 한점에서 만나는 경우에는 연산 정의가 불가하다.
여기서 알 수 있는 것은 점 덧셈의 결과를 쉽게 예측할 수 없다는 것이다.
$A+C$ 는 중앙에, $B+C$ 는 왼쪽에 있다.
즉 비선형 연산이다.
- 선형 연산이려면, 특정 대상을 basis로 더하고 곱하여 만들 수 있어야 한다.
- $f(au + v) = af(u) + f(v)$
- 벡터, 함수 등등
- 이 타원 곡선 덧셈 연산은 "순환"하는 특징이 있다.

점 덧셈 성질

위에서 정의한 타원 곡선의 점들 사이의 덧셈은 일반 덧셈과 같이 다음의 성질을 만족한다.

항등원 존재
역원 존재
교환 법칙 성립
결합 법칙 성립

항등원

I + A = A

항등원이란 위를 만족하는 점이 있다는 말이다.
예컨데 일반 덧셈이라면 0과 같은 값이 될 것이다.
위 타원 곡선에서 정의된 연산의 경우 "무한원점" 이라고 정의된 것을 항등원이라 한다.
엥? 이게 왜 무한대가 말이 되는거지? 생각해보자.

무한 원점

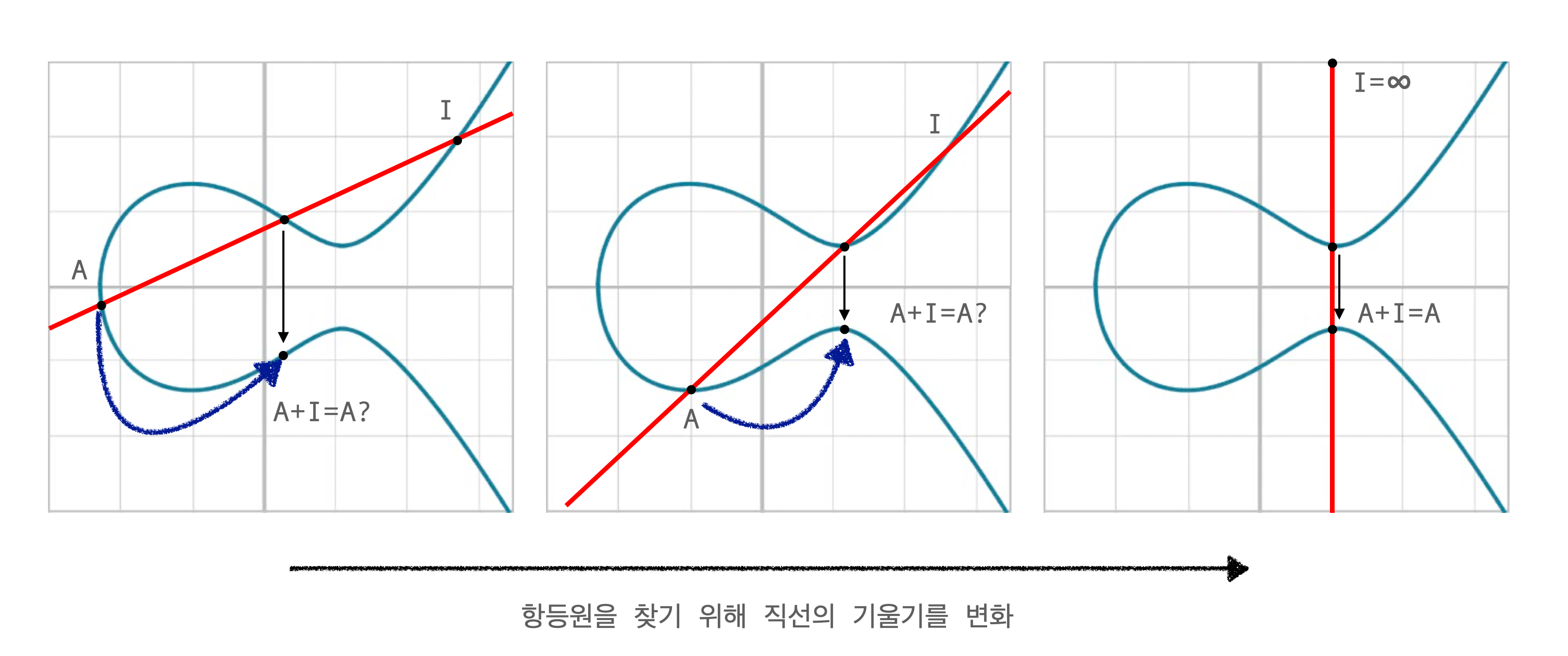
항등원의 정의에 따라 $I+A=A$ 가 되기 위해 어떠한 상태가 되어야 하는지 추적해보자.
파란색 화살표와 같은 방향으로 이동하는 것이 목표이니, 결국은 y축과 평행한 직선이 될 수 밖에 없다.
이렇게 되었을 시 I의 위치를 보면 결국 무한히 떨어져 있는 점이다.
실제로 있을지 모르지만, 이러한 점의 존재를 설정한 것이 "무한 원점"이라고 할 수 있다.

역원

A + (-A) = I

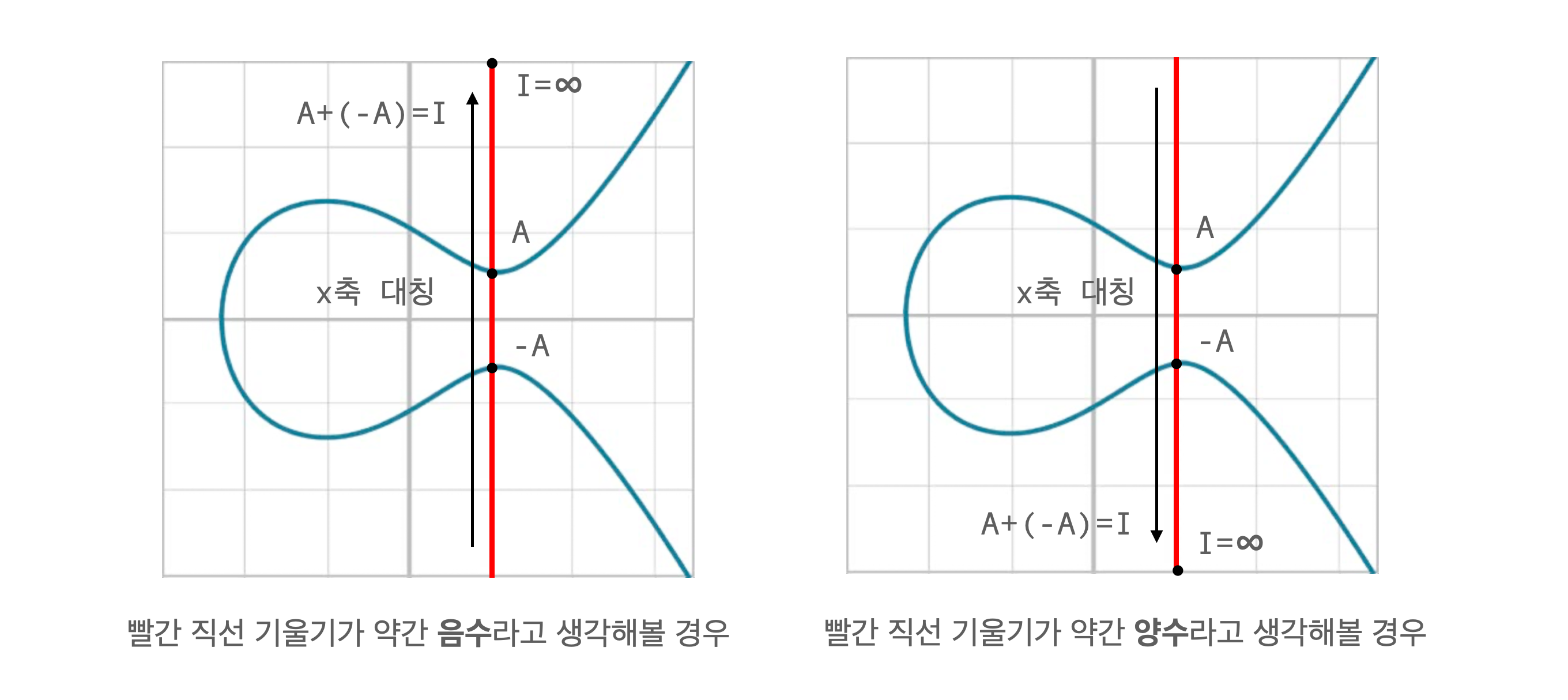
역원의 경우 위의 식에서 -A를 만족하는 것이 있는지 확인해보면 된다.
이를 위해서 항등원의 존재를 파악했던 그림을 가져오자.
무한 원점의 위치를 파악하기가 어려우니, 빨간 직선의 기울기를 약간 양수, 약간 음수라고 마음속으로 생각해보자.
그럴 경우 각각의 양 끝단에 무한 원점이 위치하고,
위의 연산을 만족하기 위해서 -A가 직관적으로 정의됨을 확인할 수 있다.

교환법칙

A+B = B+A

점 덧셈의 양 항의 순서를 변경해도 결과가 같다.
이는 조금만 선을 그어보면 확인할 수 있으니 생략한다.

결합법칙

(A+B)+C = A+(B+C)

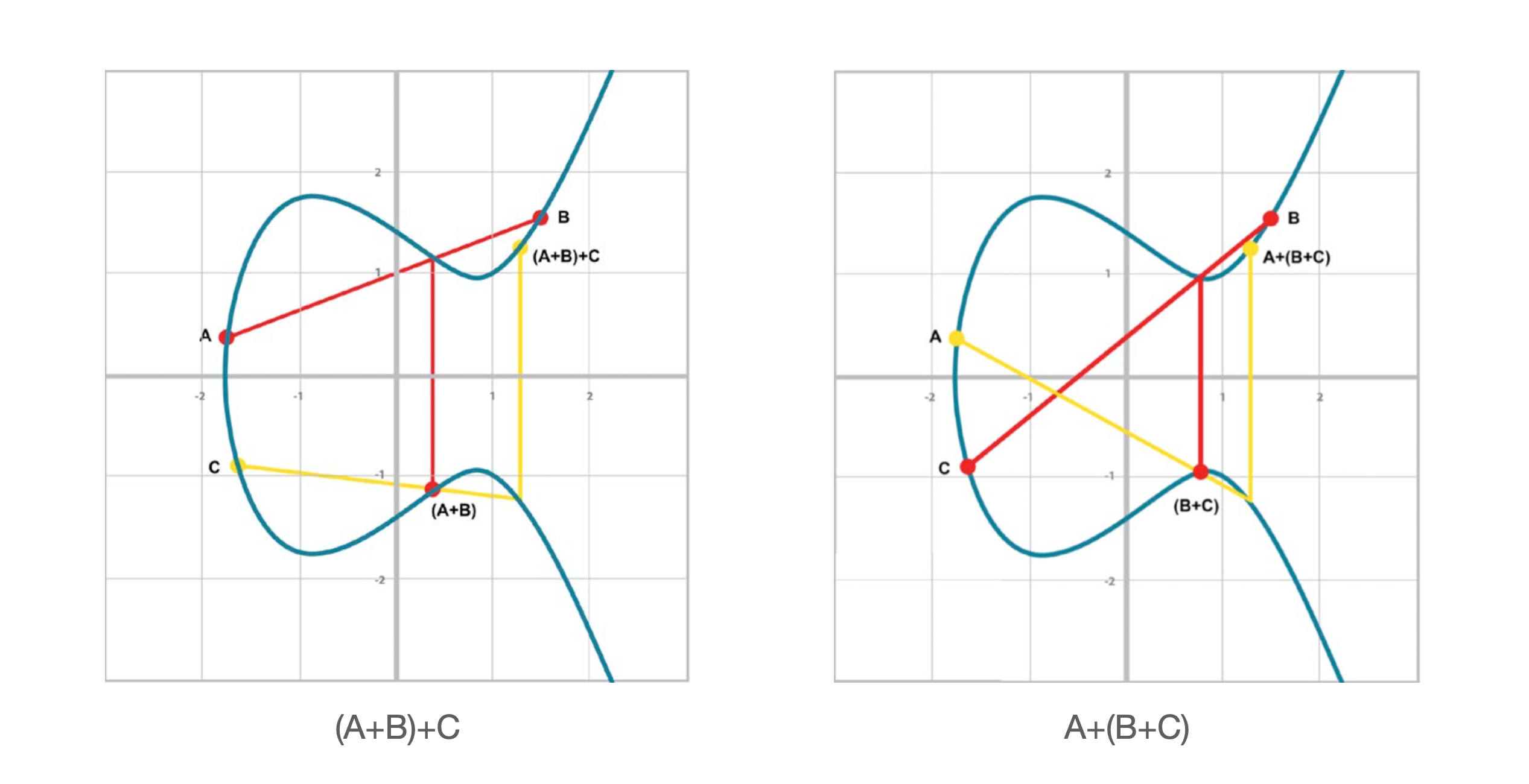
3개 이상의 덧셈에서 어느 두항을 먼저 더해도 결과는 동일하다.
위의 예시를 보고 직접 확인해보자.

코드 구현

예외 케이스가 어떤 것이 있는지를 확인해보고 고려해야할 것을 정리해보자.

더하는 두 점이 놓여있는 상황은 다음의 경우가 전부다.

두 점이 y축과 평행한 직선 위에 있는 경우
두 점이 y축과 평행한 직선 위에 있지 않은 경우
두 점이 같은 경우
- 접하는 경우

Code

무한대 표현 방법이 없어 None을 무한 원점이라고 가정할 것이다.

class Point:

    def __init__(self, x, y, a, b):
        self.a = a
        self.b = b
        self.x = x
        self.y = y

        if self.x is None and self.y is None:
            return

        if self.y**2 != self.x**3 + a * x + b:
            raise ValueError('({}, {}) is not on the curve'.format(x, y))

    def __eq__(self, other):
        return self.x == other.x and self.y == other.y \
            and self.a == other.a and self.b == other.b

    def __ne__(self, other):
        return self.__eq__(other) == False

    def __repr__(self):
        if self.x is None:
            return 'Point(infinity)'
        else:
            return 'Point({},{})_{}_{}'.format(self.x, self.y, self.a, self.b)

    def __add__(self, other):
        if self.a != other.a or self.b != other.b:
            raise TypeError('Points {}, {} are not on the same curve'.format
            (self, other))

        # A + I = A (I는 무한원점 == None으로 표현)
        if self.x is None:
            return other
        if other.x is None:
            return self

        # 두 점이 다른 경우 (y축 평행 O)
        if self.x == other.x and self.y != other.y:
            return self.__class__(None, None, self.a, self.b)

        # 두 점이 다른 경우 (y축 평행 X)
        if self.x != other.x:
            x1, y1 = self.x, self.y
            x2, y2 = other.x, other.y
            s = (y2-y1)/(x2-x1)
            x3 = s**2-x1-x2
            y3 = s*(x1-x3)-y1
            return self.__class__(x3, y3, self.a, self.b)

        # 두 점이 같은 경우(접하는 경우)
        if self == other:
            x1, y1 = self.x, self.y
            x2, y2 = other.x, other.y
            a = self.a
            s = (3*x1**2+a)/(2*y1)
            x3 = s**2-2*x1
            y3 = s*(x1-x3)-y1
            return self.__class__(x3, y3, self.a, self.b)
        
        # 두 점이 같은 경우(접하는데 그 점이 y가 0인 경우 - Divied by zero)
        if self == other and self.y == 0:
            return self.__class__(None, None, self.a, self.b)

        raise NotImplementedError