Elliptic Curve In Finite Field

최완식·2023년 1월 16일
Binary ExpansionBitcoinCryptographyElliptic CurveFinite FieldGroup
0

Bitcoin Programming

목록 보기
3/8
post-thumbnail

타원 곡선을 알아보았다면, 이걸 토대로 암호를 만들어보자.

유한체에서 정의된 타원 곡선

  • 2장에서 보았던 타원 곡선은 "실수체"에서 정의되었다.
    • 무한집합
  • 그렇기 때문에 꽉 찬 곡선으로 보였던 것
  • 이제 이 정의되는 공간을 유한체로 바꿀 것이다.
  • 먼저 유한체는 실수체와 집합의 성격(유한/무한)만 다를 뿐 다른 특징은 그대로 갖는다.
    • 즉, 쉽게 말해 사칙연산에 대해 닫혀있는 "체"의 특성을 갖는다.
  • 여기서 유용하게 쓰일만한 개념은,
  • 앞에서 배운 점 덧셈의 연산이 어떤 체에서 정의되는 지와 관계없이 유지된다는 것이다.
  • 즉, 체가 변화하면서 일반 덧셈 -> 모듈러 덧셈 과 같이 변화하는 것을 제외하면,
  • 타원 곡선 위에서 추가적으로 정의한 "점 덧셈" 역시 적용된다는 것이다.

예시

y2=x3+7y^2 = x^3 + 7
  • F103F_{103}에서 정의된 위 타원 곡선을 생각해보자.
  • 일단 특정 값을 넣어 속하는지 파악하는 방법부터 알아보자.
  • (17,64)(17, 64)를 생각해보자.
y2=642%103=79x3+7=(173+7)%103=79y^2 = 64^2 \% 103 = 79 \\ \\ x^3 + 7 = (17^3+7) \% 103 = 79
  • 값을 넣어서 계산할 시의 연산 방법을 모듈러 연산으로 처리하고 있다.
  • 그게 차이점의 전부다.
  • 이런 연산 방식을 적용했을 때, 실제 그려지는 점들은 어떤 분포를 가질까?

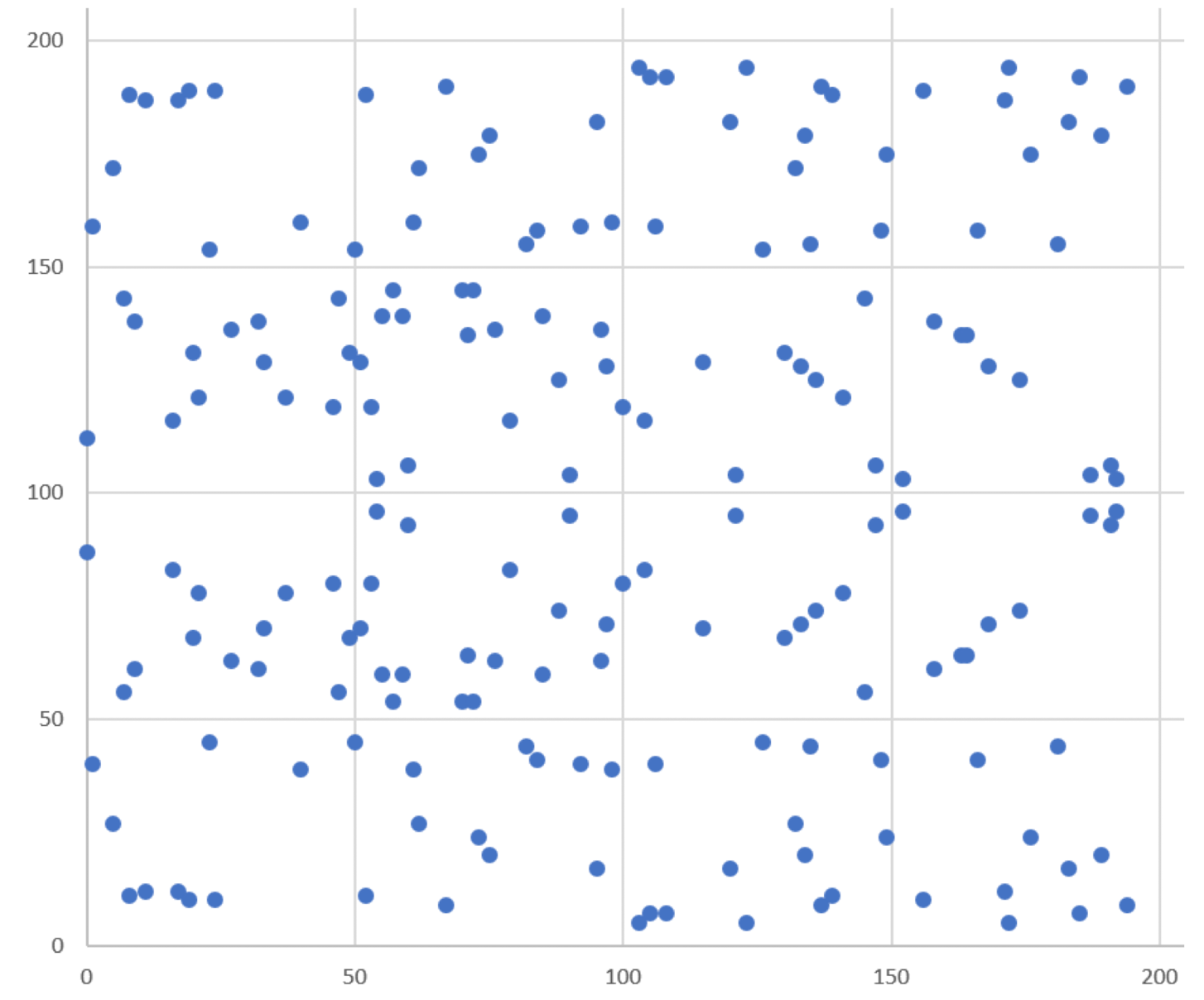
  • 산재된 모습이다.
  • y=100y = 100을 기준으로 대칭이다.
    • 엄밀히 말하면 y<0y<0 부분은 정의되지 않으므로 이것도 아니다.
  • 함수값만 일치하면 되기 때문에 산점도에서 어떠한 통찰을 얻기는 어렵다.
  • 다만 그럼에도 점 덧셈은 사용할 수 있다는 것이 중요하다.

유한체 원소를 타원곡선에 넣어보기

  • 들어가는 원소가 실수에서 유한체의 원소로만 변경되면 된다.
  • 이를 하기 위해서 우리는 FieldElement의 각 사칙 연산(+, -, *, **)등을 정의했었다.
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)

x1 = FieldElement(170, prime)
y1 = FieldElement(142, prime)
x2 = FieldElement(60, prime)
y2 = FieldElement(139, prime)

print(Point(x1, y1, a, b) + Point(x2, y2, a, b))
Point(FieldElement_223(220),FieldElement_223(181))_FieldElement_223(0)_FieldElement_223(7)
  • 각각에 인자로 들어갔던 x, y, a, b가 모두 유한체의 원소로 대치되었다.
  • 결과도 유한체의 원소를 사용한 결과로 나왔다.
  • 유한체끼리의 연산에 대해 명시적으로 적용했기 때문에 즉각 적용가능한 결과이다.

타원 곡선 위의 점들의 스칼라 곱셈

  • 스칼라 곱셈이란, 크기에 관한 요소를 각 벡터 컴포넌트에 곱하는 것을 말한다.
  • 2장에서 우리는 Point끼리의 덧셈을 정의했었다.
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)

x1 = FieldElement(170, prime)
y1 = FieldElement(142, prime)
x2 = FieldElement(60, prime)
y2 = FieldElement(139, prime)

result = Point(x1, y1, a, b)
  • 어떠한 result라는 변수가 있을 때, result를 더한 것을 3result라는 변수에 담을 수 있다.
result2 = result + result
result3 = result + result + result 
...
  • 이렇게 같은 것을 여러번 더하는 경우 굳이 이런 표현 형태를 사용하지 않고 3⋅result3 \cdot result와 같은 형태로 쓰자고 약속할 수 있다.
  • 이를 스칼라 곱셈이라 한다. 점 덧셈은 결합법칙이 성립하기 때문에 이렇게 스칼라 값을 곱할 수 있다.
  • 코드로 구현하자면 특정 상수 (이 경우에는 유한체의 원소(FieldElement)가 아니다.)가 들어왔을 때 어떻게 연산할지를 정의해주면 되겠다.
def __rmul__(self, coefficient):
    coef = coefficient
    current = self
    result = self.__class__(None, None, self.a, self.b)
    while coef:
        if coef & 1:
            result += current
        current += current
        coef >>= 1
    return result
  • 이 코드를 보다보면 "응? 왜 result를 무한원점으로 가정하지?" 라는 의문이 들수 있다.
  • 이는 아래에서 설명하겠다.

스칼라 곱셈의 결과

  • 일단 스칼라 곱셈의 결과가 어떻게 나오는지 확인해보자.
  • F223F_{223}에 대해 y2=x3+7y^2 = x^3 + 7 위의 점 (170, 142)에서의 곱셈 결과이다.
  • 왼쪽의 숫자는 스칼라 곱셈 계수를 나타낸 것이다.

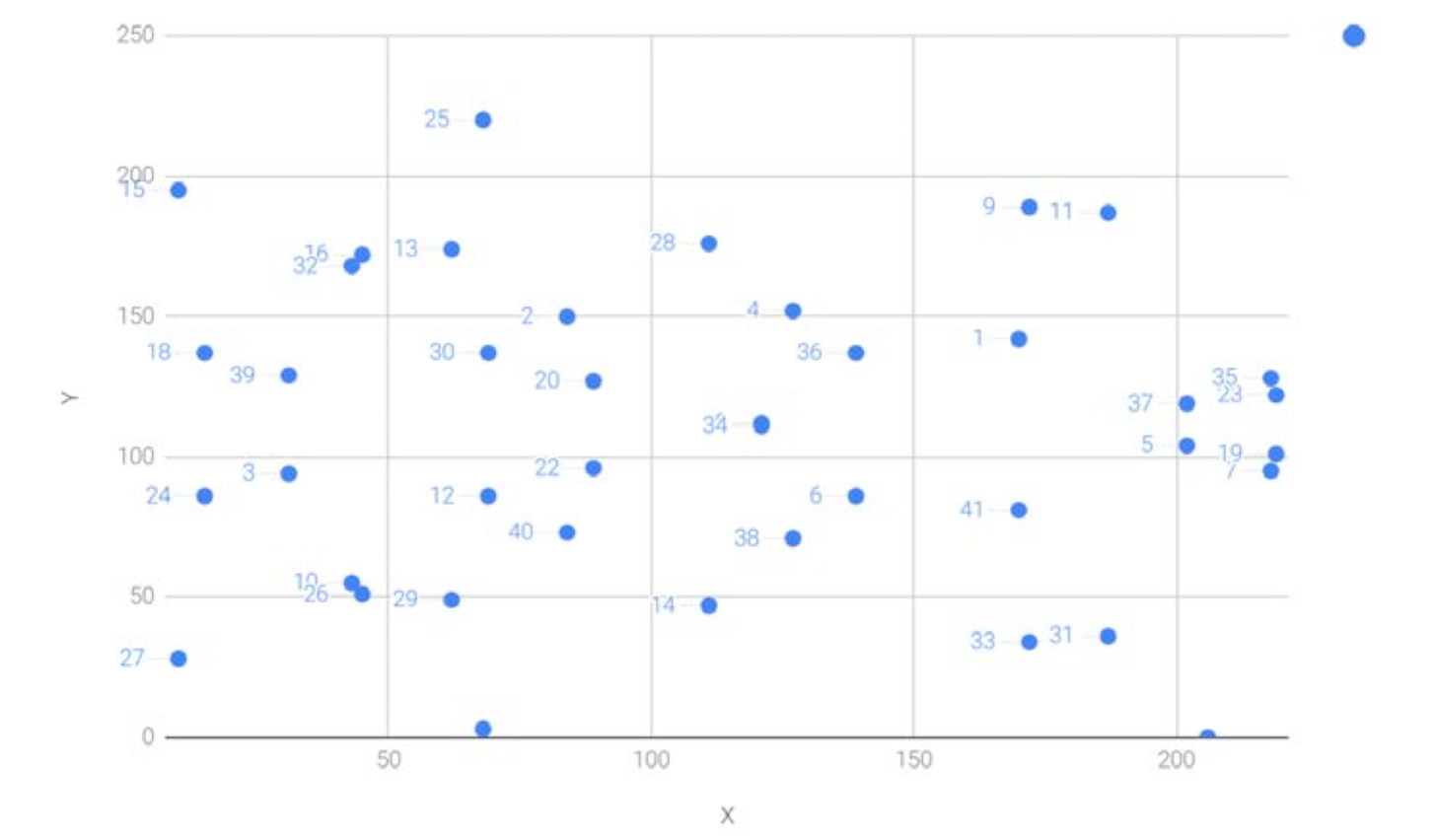
  • 보면 1이 오른쪽 중간에, 2가 왼쪽 중간에 있다.
  • 점 덧셈 자체가 "비선형" 연산인데, 그걸 n번 적용했기 때문에 더 비선형이다. 엄청나게 흩어져 있다.
  • 곱셈은 단순히 계산하면 되긴 한데, 저 점의 결과를 보고 스칼라 계수로 나눠, 어떤 점에서 부터 왔는지 찾는 것은 어렵다.
  • 즉, 점 나눗셈은 어려운 연산이다. (일방향 함수)
  • 이 점이 타원곡선 암호 방법의 원리이다.
  • 이산 로그 문제라 알려져 있다.

스칼라 곱셈의 성질

  • 자, 이제 위에서 왜 무한히 스칼라 곱을 했을 때의 결과를 무한 원점이라 가정하고 연산을 구현했는지 설명하겠다.
  • 엄밀한 증명은 아니고 사고 실험정도라 생각해주면 되겠다.
  • 일단 결론은 스칼라 값을 계속 증가시켜서 곱하는 경우 무한원점에 도달하게 된다. 이를 수학적으로 "군"을 이룬다고 한다.
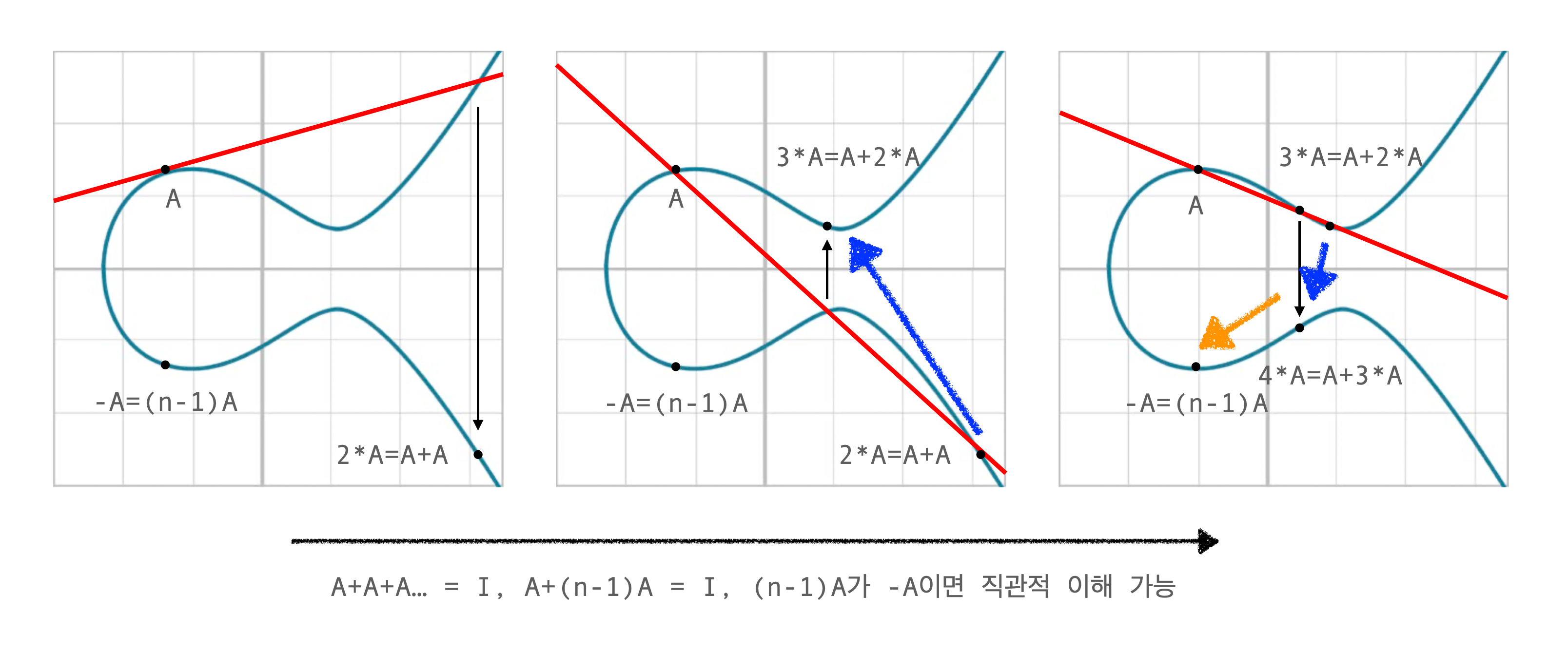
A+A+A...=IA+lim⁡n→∞(n−1)A=Ilim⁡n→∞(n−1)A=−AA+A+A... = I \\ A+ \lim_{n \to \infty}(n-1)A = I \\ \lim_{n \to \infty}(n-1)A = -A

  • 특정 A에 대해 점이 어떤식으로 이동할 수 있는지 한번 그림으로 보면 위와 같다.
  • 연산이 진행됨에 따라 점이 −A-A쪽으로 이동한다.
    • 엄밀한 증명은 지식의 범위를 넘어선다..
  • 이렇게라도 이해하고 넘어가는 게 좋다고 생각하여 추가한다.

유한군

  • 어떤점 G에 스칼라 곱셈을 키워가면서 했을 때 나오는 집합에 대해 생각해보자.
G,2G,3G,...,nGnG=0{G, 2G, 3G, ..., nG} \\ nG = 0
  • n을 무한히 키울 경우 다다르는 점은 항등원, 즉 무한원점이며 0이라 볼 수 있다.

왜 이산 로그 문제인가?

  • 스칼라 곱셈은 "점 덧셈"을 여러번 한 것을 표현한 결과라 할 수 있다.
  • 그런데 여기서 "점 덧셈"은 우리가 편의를 위해 만들어낸 연산일 뿐이다.
  • 굳이 "+"기호를 통해 표현한 것일 뿐이라는 말이다.
  • 이 연산을 "점 곱셈"이라고 말해도 전혀 무방하다. 본질은 같기 때문이다.
  • 그리고 이 점 곱셈을 연속해서 적용한다면, 그 형태는 지수가 될 것이다.
    • 덧셈 연속 -> 상수를 곱하는 꼴
    • 곱셈 연속 -> 지수 꼴
  • 어떤 점 P를 7번 "연산"한 결과를 수식으로 적어보자.

점 덧셈으로 정의한 경우

7P=QP/Q=77P = Q \\ P/Q = 7

점 곱셈으로 정의한 경우

P7=QlogPQ=7P^7 = Q \\ log_{P}Q = 7

정리

  • 본질은 같다는 것을 알 수 있다. 이건 우리가 새롭게 정의한 연산이기 때문이다.
  • 보통 지수꼴로 정리하는 경우가 많아 "이산 로그 문제"라 알려져 있다.
  • 하지만 본질은 같다. "점 덧셈"이라는 연산을 여러번 곱했을 때 발생하는 비예측성때문에 방정식 해석의 시간이 달라짐을 말하고 있다. (역산의 어려움)

유한순환군

G,2G,3G,...,nGnG=0{G, 2G, 3G, ..., nG} \\ nG = 0
  • 유한체에서 정의한 타원곡선에 대해 배웠다.
  • 그리고 여기서 특정 점을 잡고, 스칼라 곱셈을 할경우 나오는 원소들을 묶어 "군"이라 칭한다고 했다.
  • 이렇게 한 점에 스칼라 값을 곱해서 나오는 군을 "유환순환군"이라 한다.
  • 그리고 그 한 점을 "생성점"이라 한다.
  • 실제로 공개키 암호에서 사용하는 것은 유환순환군이다.

군의 특징

  • 하나의 연산에 대해서 닫혀있다.
    • 체: 사칙연산에 대해서 닫혀있었음
  • 항등원이 존재한다.
    • 무한 원점
    • 앞에서 주구장창 설명했다.
  • 군에 대해 닫혀있다.
    • aG+bG=(a+b)G?aG + bG = (a+b)G?에 대한 문제를 풀면된다.
      • 단 a, b는 n(위수)보다 작다.
    • 이건 쉬운데, (a+b)가 n보다 큰경우, 작은 경우에 따라 증명하면된다.
    • 크다면 위수에 의해 나누어진 나머지 원소로 떨어질 것이기 때문에 문제 없다.
    • 작다면 당연히 군안에 들어있으니 문제 없다.
    • 자세한 증명은 책을 보자.
  • 역원이 존재한다.
    • 이것도 앞에서 그림으로 봤었다. 무한원점을 만들어주는 역원이 항상 존재했다. (그래프에서 x축 대칭점)
  • 교환법칙 성립
  • 결합법칙 성립

Binary Expansion

  • 이제 왜 초기값을 무한 원점으로 설정하고 스칼라 곱셈을 구현했는지는 알 수 있다.
  • 그런데 스칼라 곱셈의 상수가 매우 큰 숫자라면 루프를 매우 많이 돌아야 한다.
  • 여기서 곱하는 지수를 이진수로 바꾼다면, O(n)을 O(log(n))으로 바꿀 수 있다.
def __rmul__(self, coefficient):
    coef = coefficient
    current = self
    result = self.__class__(None, None, self.a, self.b)
    while coef:
        if coef & 1:
            result += current
        current += current
        coef >>= 1
    return result
  • 만약 상수가 5이 들어왔다고 하자. 우리는 5번만 더하면 된다.
  • 이 숫자는 이진수로 101(2)101_{(2)}이다. 다음의 알고리즘으로 했을 때 5번 더하는 결과가 나오는지 확인해보자.
  • 가장 끝부터 읽어보자.
    • 1 (1*1)
      • 더하고 싶은 숫자를 한번만 더해 결과에 넣는다. (result = G)
      • 다음 자리수를 위해 더할 숫자를 2배 한다. (더하기) (addNumber = 2G)
    • 0 (11 + 20)
      • 더하면 안되므로 결과에 더하지 않는다. (result = G)
      • 다음 자리수를 위해 더할 숫자를 2배 한다. (더하기) (addNumber = 4G)
    • 1 (11 + 20 + 4*1)
      • 더하고 싶은 숫자를 한번만 더해 결과에 넣는다. (result = 5G)
      • 다음 자리수를 위해 더할 숫자를 2배 한다. (더하기) (addNumber = 8G)
    • 다음 자리수가 없으므로 종료한다.
    • 결과를 반환한다.
  • 원래 같으면 5번 루프 돌것을 3번에 끝냈다.

Reference

profile
최완식
Goal, Plan, Execute.
이전 포스트

Elliptic Curve

다음 포스트

Signature Algorithm

0개의 댓글