
<문제>
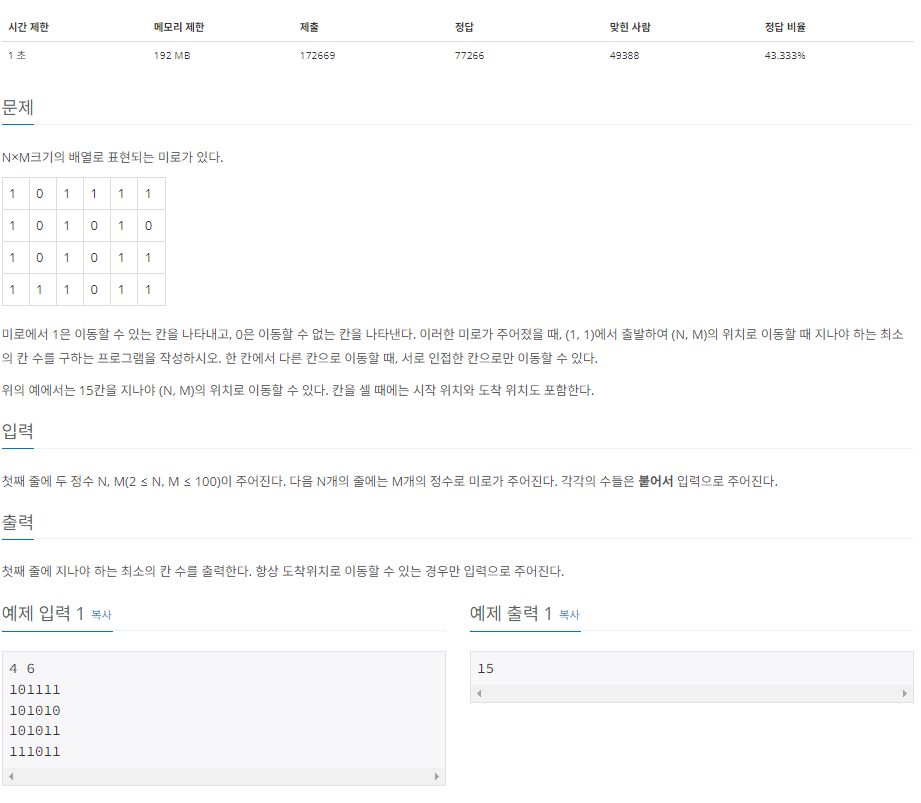
출처 : https://www.acmicpc.net/problem/2178
<나의 풀이>
package backjoon;
import java.awt.Point;
import java.util.*;
public class 미로탐색 {
// [단계 1] 받아 줄 값 세팅하기.
static int n, m; // n*m 미로
static int[][] arr; // 미로를 담아줄 배열
static boolean[][] visited; // 방문 여부 확인
static int[] dx = {-1, 1, 0, 0}; // x 방향 상하좌우
static int[] dy = {0, 0, -1, 1}; // y방향 상하좌우
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n][m];
visited = new boolean[n][m];
sc.nextLine(); // buffer 비워주기
// 배열에 값 담아주기
for (int i = 0; i < n; i++) {
String line = sc.next(); // 값을 한 줄로 받아옴
for (int j = 0; j < m; j++) {
arr[i][j] = line.charAt(j) - '0'; // 아스키코드 정수로 변환
}
}
// [단계 1] 종료.
// [단계 3] bfs 알고리즘에 시작 위치 넣어주기.
bfs(0, 0); // 시작위치
// [단계 3] 종료.
// [단계 4] 값 출력해주기.
// bfs 를 거치고 나면 도착할 칸의 행렬의 값은 거쳐야 할 최소 칸의 수가 되므로
System.out.println(arr[n - 1][m - 1]); // 마지막 칸의 인덱스로 값을 출력해주기.
// [단계 4] 종료.
}
// [단계 2] bfs 알고리즘 짜기
static void bfs(int x, int y) {
// Queue 생성
Queue<Point> queue = new LinkedList<>();
queue.offer(new Point(x, y));
visited[x][y] = true; // 방문처리
while (!queue.isEmpty()) {
Point currentPoint = queue.poll();
// 현재 위치에서 사방위 이동가능여부 판별해주기
for (int i = 0; i < 4; i++) {
int nextX = currentPoint.x + dx[i];
int nextY = currentPoint.y + dy[i];
// 1. 범위 이내에 있는가?
if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m)
continue; // 범위에서 나가면 제끼기
// 2. 막힌 길인가?
if (arr[nextX][nextY] == 0)
continue; // 막힌 길이면 제끼기
// 3. 이미 방문 했나?
if (visited[nextX][nextY])
continue; // 방문했으면(true 이면) 제끼기
// 모든 조건에 해당되지 않음. 즉, 갈 수 있는 길 이면
// queue 에 삽입해주고 방문처리.
queue.offer(new Point(nextX, nextY));
visited[nextX][nextY] = true;
// 그리고 최소 칸의 수를 구해야되므로 해당하는 칸에 1씩 누적해서
// 도착 칸이면 그 값이 지나야 하는 최소 칸의 수.
arr[nextX][nextY] = arr[currentPoint.x][currentPoint.y] + 1;
}
}
}
// [단계 2] 종료.
}<다른 사람의 풀이>
개념 이해에 참고한 블로그 :
https://infodon.tistory.com/100
https://iseunghan.tistory.com/312 -> 최단거리 구할 수 있는 원리 설명해주심!
<핵심 개념>
bfs 로 최단거리의 수를 구하는 방법.
그래프로 문제를 풀 때 이동 조건에 대해 숙지하기. ( 자주 쓰이더라)
안타깝게도 dfs 로 풀면 시간초과가 난다.. 최단거리 문제는 bfs 로 푸는 것이 좋다고.
왜냐면 dfs 는 분기점이 생길 때 마다 끝까지 파고들었다가 다시 돌아와야되는 번거로움이 있어
한번 지난 노드를 다시 방문하지 않는 bfs에 비해 왔다갔다 하는 점에서 효율성이 떨어지기 때문이다.
참고 : 벨로그
<피드백>
어렵지만 한 번 익숙해지면 그래도 풀만해진다.
포기하지 않으면 뭐라도 되니 어렵더라도 포기하지 말고 풀고 복습 열심히 하자.
