[백준] 9465번 스티커 (java)

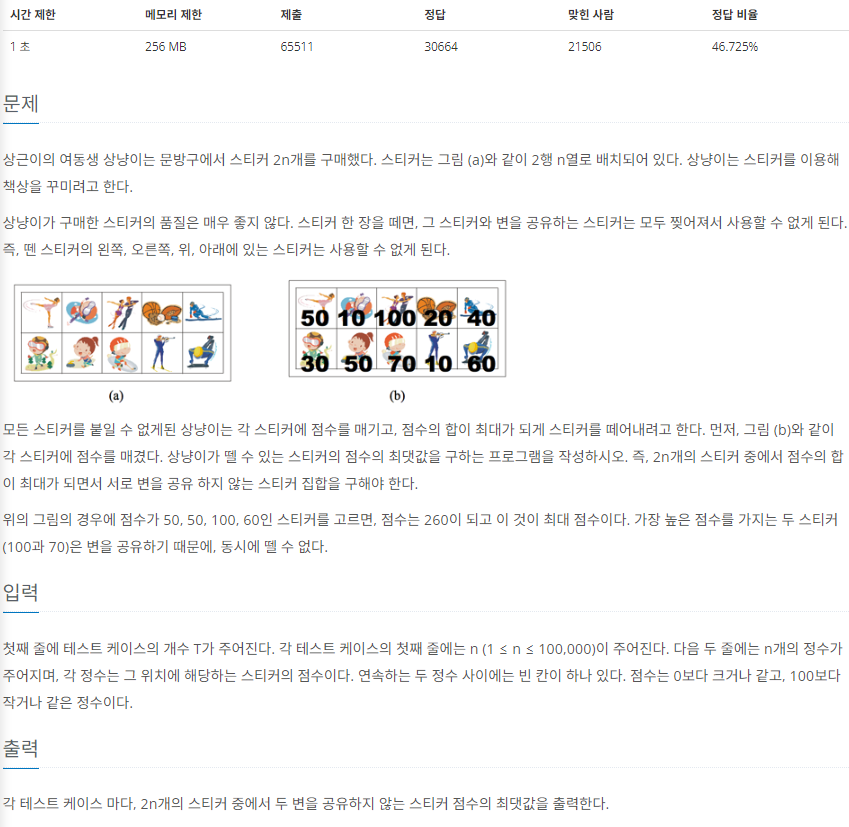
<문제>

출처 : https://www.acmicpc.net/problem/9465

<나의 풀이>

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();

        for (int i = 0; i < T; i++) {
            int rows = 2;
            int cols = sc.nextInt();
            int[][] stickers = new int[rows][cols + 1];
            int[][] dp = new int[rows][cols + 1];

            // sticker 초기화 해주기
            for (int j = 0; j < rows; j++) {
                for (int k = 1; k <= cols; k++) {
                    stickers[j][k] = sc.nextInt();
                }
            }
            // dp 테이블 초기값 세팅해주기
            dp[0][1] = stickers[0][1];
            dp[1][1] = stickers[1][1];

            // dp 순회하면서 값 채워주기
            for (int a = 2; a <= cols; a++) {
                // 첫쨰 열의 a값은 sticker에서의 a값에
                // 대각선 아래의 값과 그 옆에 값 중 큰 수
                dp[0][a] = stickers[0][a]
                        + Math.max(dp[1][a - 1], dp[1][a - 2]);
                dp[1][a] = stickers[1][a]
                        + Math.max(dp[0][a - 1], dp[0][a - 2]);

            }
            int maxScore = Math.max(dp[0][cols], dp[1][cols]);
            System.out.println(maxScore);
        }
   }
}

문제를 더 잘 이해하기 위한 블로그

<핵심 개념>

DP
아이디어를 떠올리고, 규칙을 찾고, 점화식을 도출 이란 세 가지 방법으로 심플하게 생각하면 되지만 과정은 심플해도 직접 해보면 절대 심플하지 않다..
정말 잘하는 사람들을 보면 쉬워 보인다고 하는데 DP는 유독 더 그런 것 같다.

그래도 낯설 뿐이지 모르는 건 아니다. 이해가 되기 시작하니 어느정도 보인다. 익숙해지자.

DP 는 주로 경우의 수, 자신만의 규칙이 있는 수열과도 같아서 고등학생 때 수학문제를 풀던 기억을 떠올리며 아이디어를 도출하려고 노력하는 편이다. 문과지만 수학을 제일 좋아했어서
알고리즘 풀다 수학적 개념으로 접근하면 그래도 즐겁게 풀 수 있다.
그러니 DP도 익숙해지면 재밌지않을까. 규칙을 도출하는 일은 즐거우니 말이다.

<피드백>

문제를 경우의 수로 나눠 생각해보면 그래도 풀 수 있다.
한 네번째 줄 까지 케이스를 나눠 반복해보면 규칙이 보인다.
다만 DP 문제에서

DP문제를 풀 때 구하고자 하는 수가 무엇인지, 주어진 조건으로 어떻게 구할지
쪼갤 수 있어야되고, 구한 해가 다음 문제의 해가 되어야하며, 중복되어야 된다. 는 세가지 원칙을 지켜가며 풀어야 한다.
처음 DP를 풀 때 DP로 생각해보고 아이디어를 떠올리고 규칙성을 찾고
이제 그 규칙을 DP테이블로 만들어보고 점화식을 어떻게 쓸건지 생각해야되고..
DP테이블에 초기값을 어떻게 할거며.. 인덱스를 또 주의해서 써줘야 한다.
아무튼 어려운게 맞다.

그래두 꿀팁을 적어보자면 완탐에선 등비 등차같은 일정 규칙이 있는 것 아니면 풀기 어렵다고 한다. (코드스테이츠 강의 참고)
그래서 수열, 경우의 수 등이 나오면 우선 DP를 떠올려보는 것도 좋을 것 같다.