Robust Regression
-
Robust Regression (강건 회귀) : 이상치에 영향을 제거하거나, 덜 받도록 설계된 회귀 분석 기법
-
OLS는 MSE (Mean Squared Error)를 손실함수로 사용한다. 이때, 오차가 큰 이상치의 영향이 제곱(Squared)으로 반영되어 다른 데이터에 비해 훨씬 큰 가중치를 가지게 된다. 이로 인해 모델이 일부 이상치에 크게 치우쳐져 학습되는 문제가 발생할 수 있다.
-
강건 회귀는 OLS의 가정이 제대로 만족되지 않는 상황에서 대안적으로 사용하는 회귀 방법이다. 즉 강건 회귀는 종속변수에 이상치가 많거나, 잔차가 정규분포를 따르지 않는 경우에도 모델의 안정성과 일반화 성능을 보장하는 일반화된 회귀이다.
-
강건 회귀를 구현하는 방법은 크게 세 종류로 나눌 수 있다.
-
- 손실 함수의 재정의 : Huber Loss
-
- 데이터의 부분 집합을 사용 : RANSAC (RANdom SAmple Consensus)
-
- 중앙값을 사용 : Theil-Sen Estimator
-
-
Huber Loss
- Huber Loss는 작은 오차에 대해서는 제곱 오차를 사용하고, 큰 오차에 대해서는 절대 오차를 사용한다. 이를 통해 작은 오차에는 OLS처럼 반응하지만, 이상치에 대해서는 선형적으로 반응함으로써 이상치의 영향을 줄일 수 있다.
-
잠깐 정규화를 적용한 회귀에 대해 복습해보자. 정규화를 적용하면 과적합을 방지 할 수 있는데, 이로 인해 이상치에 대한 영향을 간접적으로 줄일 수 있다. 그러나 이는 OLS와 비교하여 이상치에 덜 민감하다는 의미이고, 이상치의 영향을 크게 줄이는 역할은 하지 못한다.
- 아래 예시를 통해 HuberRegressor과 Ridge의 차이를 통해 이를 확인할 수 있다.
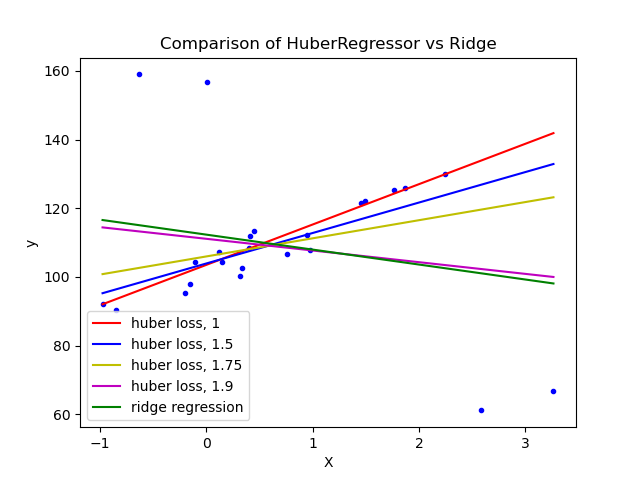
-
위 예시를 통해 적절한 임계값(δ)에 대해 생각해 볼 수도 있다.
-
임계값이 너무 작은 경우 : 거의 모든 데이터 포인트에 대해 선형 손실이 적용되어, 절대 오차 회귀(Linear L1 Regression)와 유사하게 작동한다. 이상치에 대해 강건하지만, 전체 데이터에 대해 너무 단순한 모델을 학습하게 되어 과소적합이 될 수 있다.
-
임계값이 너무 큰 경우 : Huber Loss가 MSE와 거의 같아지기 때문에 이상치에 민감하다. 즉, Huber Regression이 OLS처럼 이상치에 의해 왜곡된 회귀선을 그릴 수 있음을 의미한다.
-
-
따라서, HuberRegressor에서의 임계값은 데이터의 특성에 따라 다르게 설정되어야 하며, 일반적으로 교차 검증(cross-validation) 등을 통해 적절한 값을 찾는다.
RANSAC
-
RANSAC(RANdom SAmple Consensus) 회귀는 OLS처럼 모든 데이터를 사용하여 회귀 모델을 학습하는 대신, 무작위로 샘플링된 데이터의 부분 집합을 이용하여 모델을 학습하고, 이를 통해 이상치의 영향을 줄이는 방법이다.
-
RANSAC 회귀의 진행 과정을 scikit-learn에서의 핵심
하이퍼파라미터와 함께 살펴보자.-
- 반복적으로 샘플링 : 전체 데이터 중 일부를 무작위로 샘플링하여 모델을 학습한다. 샘플링은
max_iter만큼 반복적으로 수행되며, 각 샘플링에 대해 별도의 모델이 학습된다. 모델을 학습하기 위해 샘플링할 최소 데이터 포인트의 개수는min_samples로 설정된다.
- 반복적으로 샘플링 : 전체 데이터 중 일부를 무작위로 샘플링하여 모델을 학습한다. 샘플링은
-
- 모델 평가 : 학습된 모델을 각각 전체 데이터에 적용하여 각 데이터 포인트의 오차(residual)를 계산한다. 주어진 오차 임계값
residual_treshold이하의 데이터 포인트들을 합의 집합(consensus set, inliers)으로 설정한다. 합의 집합은 해당 모델이 잘 설명할 수 있는 데이터의 부분 집합을 나타냅니다.
- 모델 평가 : 학습된 모델을 각각 전체 데이터에 적용하여 각 데이터 포인트의 오차(residual)를 계산한다. 주어진 오차 임계값
-
- 최적의 모델 선택 : 학습된 모델들 중 가장 많은 데이터 포인트가 합의하는 모델, 즉 인 모델을 최적의 모델로 선택한다.
-
-
RANSAC의 핵심은 무작위 샘플링과 합의(consensus)를 통한 이상치 배제이다. 무작위로 샘플링된 부분 집합을 사용해 모델을 학습하고, 이 모델에 가장 잘 맞는 데이터를 통해 최적의 모델을 선택합니다. 이 과정에서 이상치의 영향이 배제되므로 이상치에 강건한 회귀 모델을 생성할 수 있다.
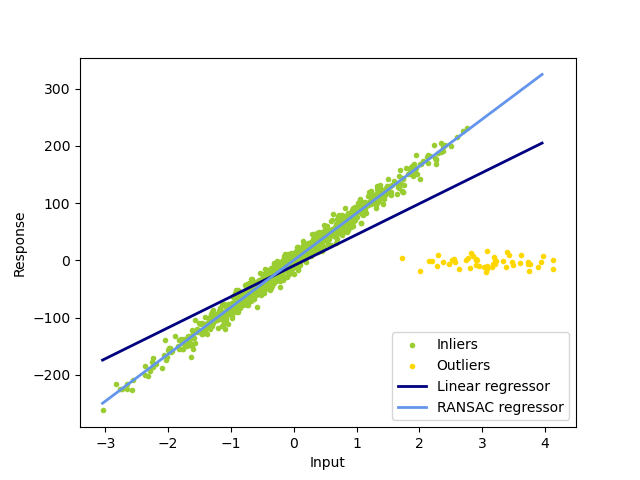
-
하이퍼파라미터에 따른 RANSAC의 특징을 살펴보자.하이퍼파라미터 (적정치 보다) 작은 경우 (적정치 보다) 큰 경우 max_trials적절한 모델을 찾을 수 없다 연산 비용이 높아진다 min_samples최소 2개의 점이 필요하다 일반적으로 모델의 신뢰성이 높아지지만, OLS의 회귀직선에 근접해진다(이상치에 민감) residual_threshold일반 데이터 포인트가 이상치로 판별될 수 있다 이상치가 합의 집합에 포함될 수 있다
-
RANSAC은 이상치 탐지에도 사용할 수 있으며, 합의 집합에 포함되지 않는 데이터 포인트들은 이상치로 간주될 수 있다.
-
RANSAC의 신뢰성은 확률론적 접근을 통해 보장되며, 무작위 샘플링이 잘 수행되지 않거나 반복 횟수(max_trials)가 충분하지 않다면 모델의 신뢰성이 떨어진다.
Theil-Sen Estimator
-
Theil-Sen Estimator는 회귀 계수를 추정하는 데 있어 비모수적(non-parametric) 방법을 사용하여 이상치에 강건한 회귀 직선을 찾는 방법이다. 기본 아이디어는 데이터 포인트 간의 모든 가능한 쌍의 기울기(slope)를 계산하고, 그 중앙값(median)을 취하여 최종 회귀선의 기울기로 사용하는 것이다.
-
기본적인 Theil-Sen의 작동 방식은 아래와 같다.
-
1. 모든 데이터 포인트 쌍의 기울기 계산 : 총 n개의 데이터 포인트 에서 가능한 모든 데이터 포인트 쌍 선택하여 기울기를 계산한다.
-
2. 기울기의 중앙값을 선택 : 총 개의 기울기의 중앙값을 최종 회귀선의 기울기로 선택한다.
-
3. 절편 계산 : 각 데이터 포인트에 대해 절편(bias)을 계산 후 모든 절편 값의 중앙값을 최종 절편으로 설정한다.
-
4. 최종 회귀선 : 데이터 포인트 쌍의 기울기 집합을 , 절편의 집합을 라고 하면 최종 회귀선은 아래와 같이 정의된다.
-
-
Theil-Sen의 경우 중앙값을 사용하여 최대 50%의 이상치 영향을 제거할 수 있으며, 비모수적 추정을 사용하기 때문에 종속변수의 분포에 대한 가정이 필요없다.
-
기본적인 작동 방식은 위와 같지만, scikit-learn의 TheilSenRegressor는 시간복잡도와 메모리 사용량을 고려하여 데이터의 부분집합을 사용한다. 관련된 하이퍼파라미터들을 살펴보자.
하이퍼파라미터 설명 (적정치 보다) 작은 경우 (적정치 보다) 큰 경우 n_subsamples부분집합의 크기 높은 강건성, 계산 비효율적 낮은 강건성, 계산 효율적 max_subpopulation부분집합에서 생성된 조합의 수가 해당 값보다 클 경우 무작위로 선택된 부분집합을 사용한다 일부 조합만 사용하여중앙값 계산 연산 비용 증대 max_iter최소제곱해들의 공간적 중앙값을 계산할 최대 반복수 충분히 수렴하지 못함 시간복잡도 증대
Tips of using Robust Regression
-
우선, scikit-learn의 "things to keep in mind when dealing with data corrupted by outliers" 를 기준으로 RANSAC과 Theil-Sen을 비교해보자.
- Theil-Sen과 RANSAC은 이상치의 영향을 완전히 지우는 방식을 사용하기 때문에 직접적인 비교가 가능하지만, HuberRegressor의 경우는 이상치의 영향을 줄이는 방식을 사용하기 때문에 직접적으로 비교할 수 없다.
-
Outliers in X or in y?
-
Outliers in X : 독립변수(X)에서 이상치가 있는 경우는 입력 피처 자체가 비정상적으로 벗어나는 경우를 의미한다. 예를 들어, 다른 데이터와 매우 다른 특이한 피처 값이 존재하는 경우를 의미한다.
-
Outliers in y : 종속변수(y)에 이상치가 있는 경우는 특정 데이터 포인트가 정상적인 독립변수 값을 가지고 있지만 결과값이 예상보다 매우 크게 벗어난 경우를 의미한다.
-
-
Fraction of outliers versus amplitude of error : 데이터셋에서 이상치가 차지하는 비율과 오차의 크기에 따라 모델 선택에 영향을 미친다
-
Theil-Sen, RANSAC이 일반적으로 좋은 상황
estimator Outliers in X or in y? Fraction of outliers Amplitude of error RANSAC y 민감하지 않음 민감하지 않음 Theil-Sen X, y 최대 50% 민감하지 않음 ※ Theil-Sen의 특성은 고차원 데이터에서는 사라질 수 있다
※ 보편적인 상황에서는 RANSAC이 가장 좋은 선택이다
-
시간 복잡도
- HuberRegressor는 샘플의 수가 매우 많은 경우()가 아니면 RANSAC 및 Theil-Sen보다 더 빠르다. 이는 RANSAC과 Theil-Sen이 데이터의 부분 집합에서 학습을 진행하기 때문이다.
- RANSAC은 Theil-Sen보다 더 빠르며, 샘플의 수가 커져도 효율적으로 작동한다.
-
잔차, 종속변수의 정규성
- Theil-Sen과 RANSAC은 비모수적 특성을 가지고 있기 때문에 종속변수나 잔차의 분포가 정규성을 따르지 않아도 매우 잘 작동한다.
- Huber Regression은 정규성 가정을 약화시키는 방식을 사용하기 때문에 잔차의 분포가 약간의 정규성에서 벗어나도 사용할 수 있지만, 잔차가 크게 왜곡된 경우에는 신뢰도가 낮다.
강건 회귀들과 OLS의 비교
- scikit-learn에서 제공하는 자료를 통해 강건 회귀 방식들과 OLS의 결과를 시각적으로 비교해보자.
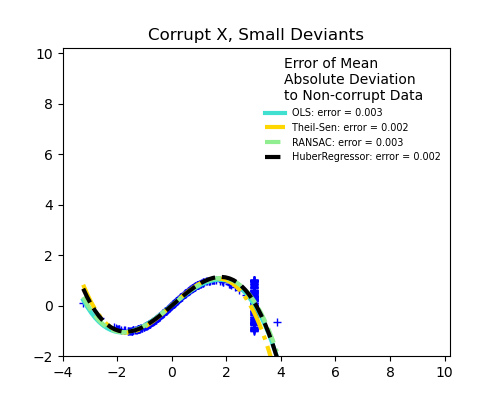
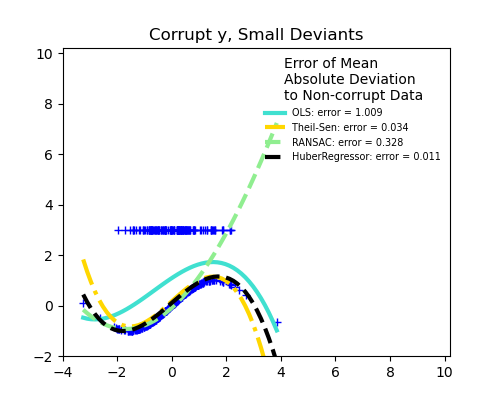
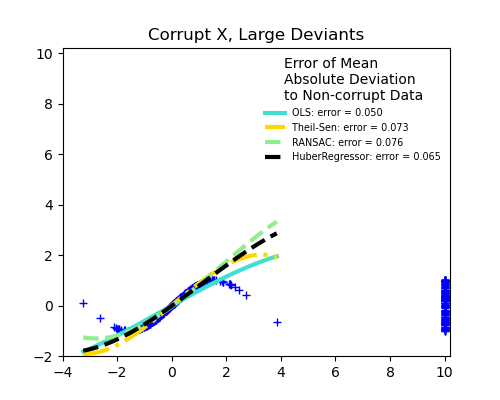
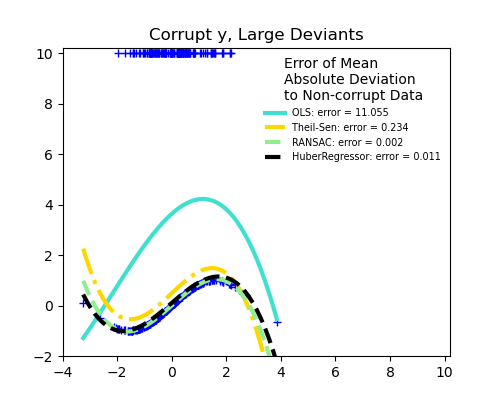
사진 출처
-
Comparison of HuberRegressor vs Ridge : HuberRegressor vs Ridge on dataset with strong outliers
-
강건 회귀들과 OLS의 비교 : Robust linear estimator fitting
