[C++] BOJ : 시간 복잡도

BOJ 24262번 : 상수 시간 복잡도 O(1)

// BOJ 24262번 : 상수 시간 복잡도 O(1)
int cnt = 0;

int TimeComplex(int n) {
	cnt++;
	return cnt; 
}

int main() {
	
	int n;
	cin >> n;
	int count = TimeComplex(n);
	
	cout << count << '\n';
	cout << 0 << '\n';
	
	return 0;
}

BOJ 24263번 : 시간 복잡도 O(n)

// BOJ 24263번 : 시간 복잡도 O(n)
int cnt = 0;

int TimeComplex(int n) {
	
	for (int i = 1; i <= n; i++) {
		cnt++;
	}
	return cnt; 
}

int main() {
	
	int n;
	cin >> n;
	int count = TimeComplex(n);
	
	cout << count << '\n';
	cout << 1 << '\n';
	
	return 0;
}

BOJ 24264번 : 시간 복잡도 O(n^2)

// BOJ 24264번 : 시간 복잡도 O(n^2) -> 제곱되면서 메모리 제한 고려 필요했음
long long cnt = 0;

long long TimeComplex(int n) {
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cnt++;
		}
	}
	return cnt; 
}

int main() {
	
	int n;
	cin >> n;
	long long count = TimeComplex(n);
	
	cout << count << '\n';
	cout << 2 << '\n';
	
	return 0;
}

BOJ 24265번 : 시간 복잡도 O(n^2)

// BOJ 24265번 : 시간 복잡도 O(n^2) -> 점화식: 1/2 * n(n-1)

long long cnt = 0;

long long TimeComplex(int n) {
	for (int i = 1; i <= n-1; i++) {
		for (int j = i+1; j <= n; j++) {
			cnt++;
		}
	}
	return cnt; 
}

int main() {
	
	int n;
	cin >> n;
	long long count = TimeComplex(n);
	
	cout << count << '\n';
	cout << 2 << '\n';
	
	return 0;
}

BOJ 24266번 : 시간 복잡도 O(n^3)

// BOJ 24266번 : 시간 복잡도 O(n^3)
long long cnt = 0;

long long TimeComplex(int n) {
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			for (int k = 1; k <= n; k++) {
				cnt++;
			}
		}
	}
	return cnt; 
}

int main() {
	
	int n;
	cin >> n;
	long long count = TimeComplex(n);
	
	cout << count << '\n';
	cout << 3 << '\n';
	
	return 0;
}

BOJ 24267번 : 시간 복잡도 O(n^3)

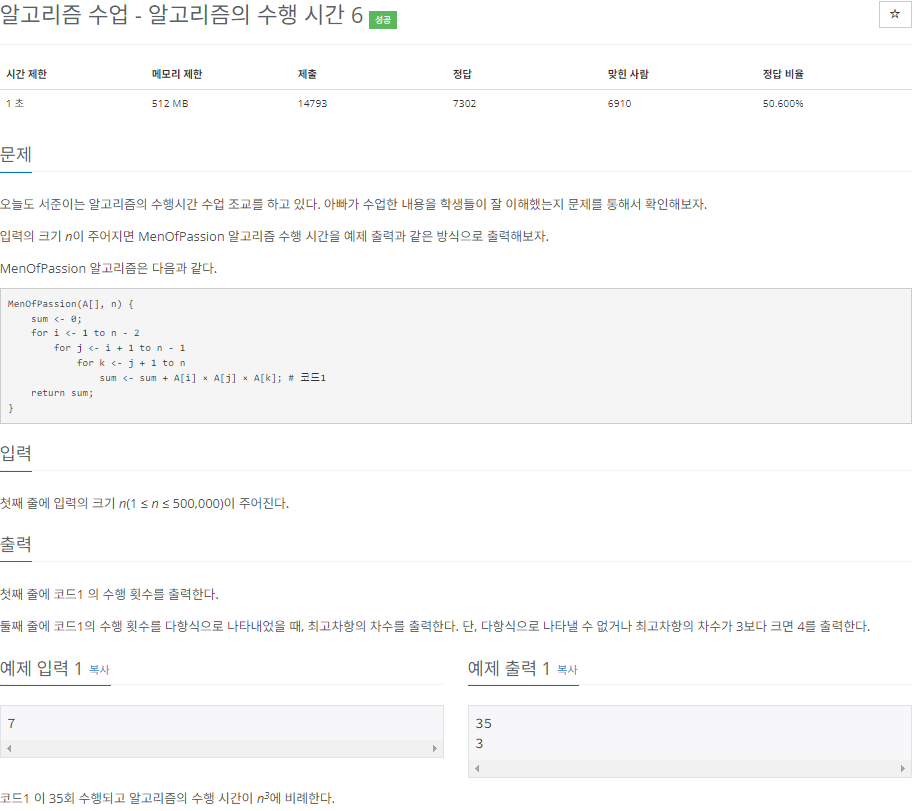
• 익명의 백준 수식 작성자분
  

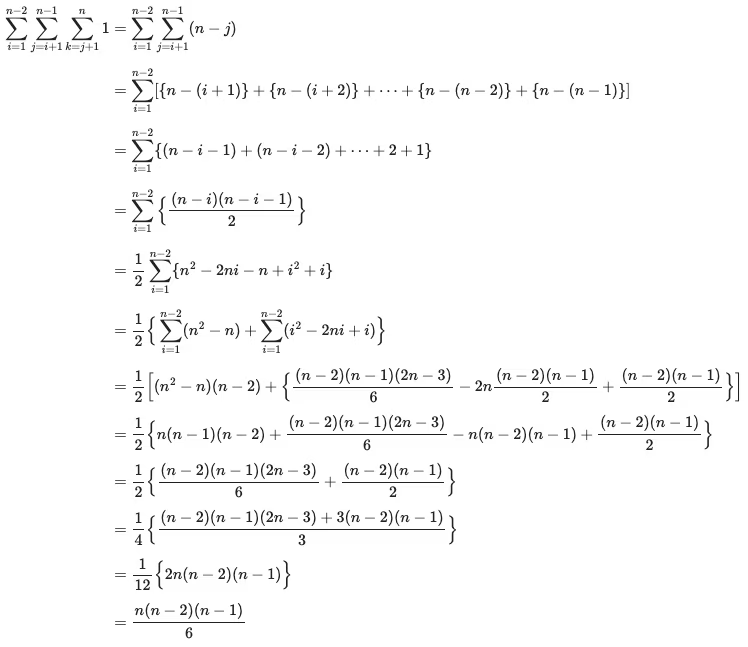
정답 코드

#include <iostream>
using namespace std;
 
int main(){
    long long n;
    cin >> n;
    cout << (n-2)*(n-1)*n/6 << '\n' << 3;
    return 0;
}

내 풀이

#include <iostream>

using namespace std;

long long int cnt = 0;

long long int TimeComplex(int n) {
		
	if (n == 1) return 0;
    // n = 2였을때도 return이 0이었어야 함
	
	long long int A[n-2] = { 0 };
	long long int sum = 0;
	for(int i = 1; i <= n-2; i++) {
		sum += i;
		A[i-1] = sum;
	}
	long long int answer = 0;
	for (int i = 0; i < n-2; i++) {
		answer += A[i];
	}
	
	return answer; 
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
	int n;
	cin >> n;
	long long int count = TimeComplex(n);
	
    // output은 건들지 말고 3으로 고정 출력했어야 함
    // 이러나 저러나 최악의 시간 복잡도 O(n^3) 이기 때문이다.
	int output = 0;
	if (count == 0) {
		output = 0;
	} else output = 3;
	
	cout << count << '\n';
	cout << output << '\n';
	
	return 0;
}

BOJ 24313번 : 시간 복잡도

int TimeComplex(int a1, int a0, int c, int n0) {
		
	int result;
	
	int fn0_answer = a1 * n0 + a0; // 음수가 나올 수 있음
	int gn0_answer = c * n0; 	   // 항상 양의 정수
	
	if (fn0_answer <= gn0_answer && c >= 0 && n0 >= 0) {
		result = 1;
	} else result = 0;
	
    // n >= n0 이어야 하기 때문에 이를 만족하는 함숫값을 계산해야함
	for (int i = n0; i <= 100; i++) {
		int fi_answer = a1 * i + a0;
		int gi_answer = c * i;
		
		if (fi_answer > gi_answer) {
			result = 0;
			return result;
		}
	}
	
	return result; 
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
	int a1, a0, c, n0;
	cin >> a1 >> a0;
	cin >> c;
	cin >> n0;
	
	int result = TimeComplex(a1, a0, c, n0);
	
	cout << result << '\n';
	
	return 0;
}