1. 비지도 학습
- 타깃이 없을 때 데이터에 존재하는 패턴이나 데이터 구조를 파악하기 위해 사용하는 머신러닝 알고리즘
- 사람이 가르치지 않아도 데이터의 무엇인가를 학습
1.1. 군집 알고리즘
1.1.1. 실습
-
데이터 준비
-
데이터의 수=300, 이미지의 크기=100 X 100
-
첫 번째 이미지에 대한 배열 값을 출력(0 ~ 255 사이의 정수값)
-
0에 가까울수록 검정색으로 나타난다

-
넘파이 배열로 저장된 이미지를 시각화
-
흰 배경을 검정색으로 변환하고 실제 사과 부분을 밝은색으로 바꾼 상태이다.
-
원래는 배경이 흰색, 물체가 검정색에 가깝다.
-
그 이유는 배경과 물체 중에 더 중요한 물체에 집중하기 위해 배경을 검정, 물체를 흰색에 가깝도록 변환한 것이다.
-
알고리즘이 어떤 출력을 만들기 위해 곱셈, 덧셈을 한다.
-
픽셀값이 0이면 출력도 0이되어 의미가 없다. 픽셀 값이 높으면 출력값도 커지기 때문에 의미를 부여하기 좋다.

-
cmap='gray_r'을 활용하여 밝은 부분이 0에 가깝고, 어두운 부분이 255에 가깝도록 변환하였다.

-
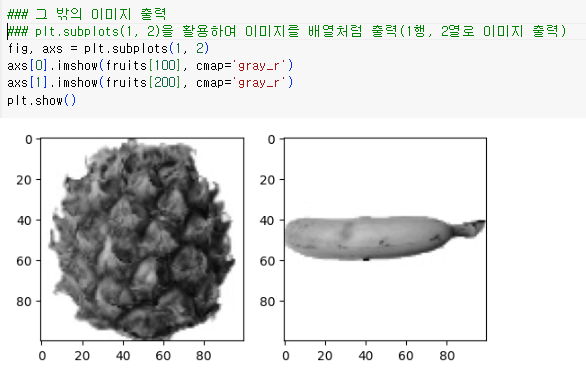
그 밖의 이미지 출력
-
plt.subplots(1, 2)을 활용하여 이미지를 배열처럼 출력(1행, 2열로 이미지 출력)
-
픽셀값 분석
-
첫번째 차원을 -1로 할당하면 자동으로 남은 차원을 할당

-
샘플마다 픽셀의 평균값을 계산하기 위해 mean()메서드 사용 -> 사과 샘플 100에 대한 픽셀 평균 값을 구한다
-
axis 인수 : 배열의 축을 의미, axis=1은 열을 계산, axis=0은 행을 계산
-
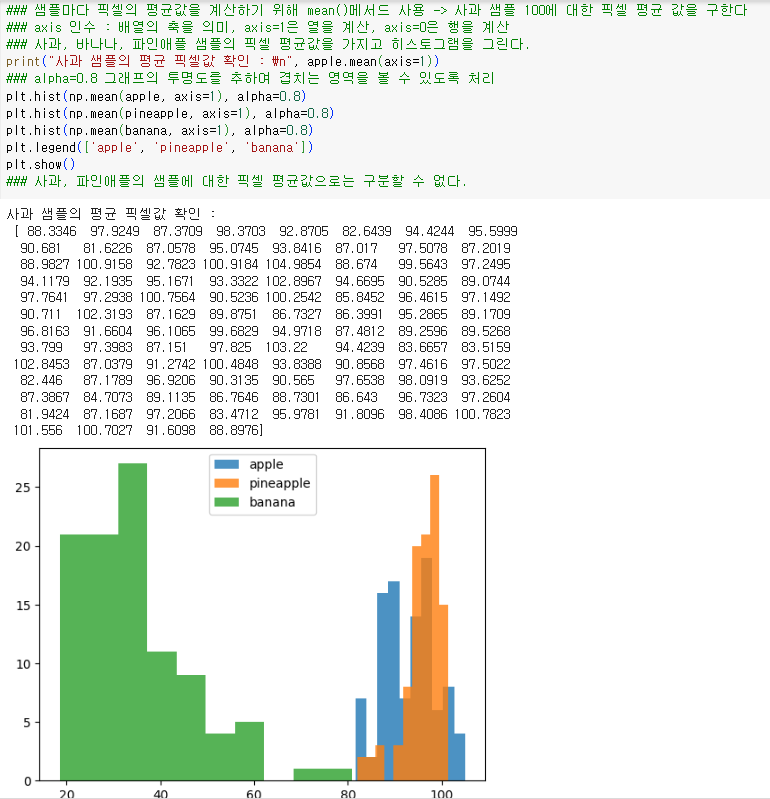
사과, 바나나, 파인애플 샘플의 픽셀 평균값을 가지고 히스토그램을 그린다.
-
alpha=0.8 그래프의 투명도를 추하여 겹치는 영역을 볼 수 있도록 처리
-
사과, 파인애플의 샘플에 대한 픽셀 평균값으로는 구분할 수 없다.
-
샘플의 평균 값이 아닌 픽셀 별 평균값을 확인
-
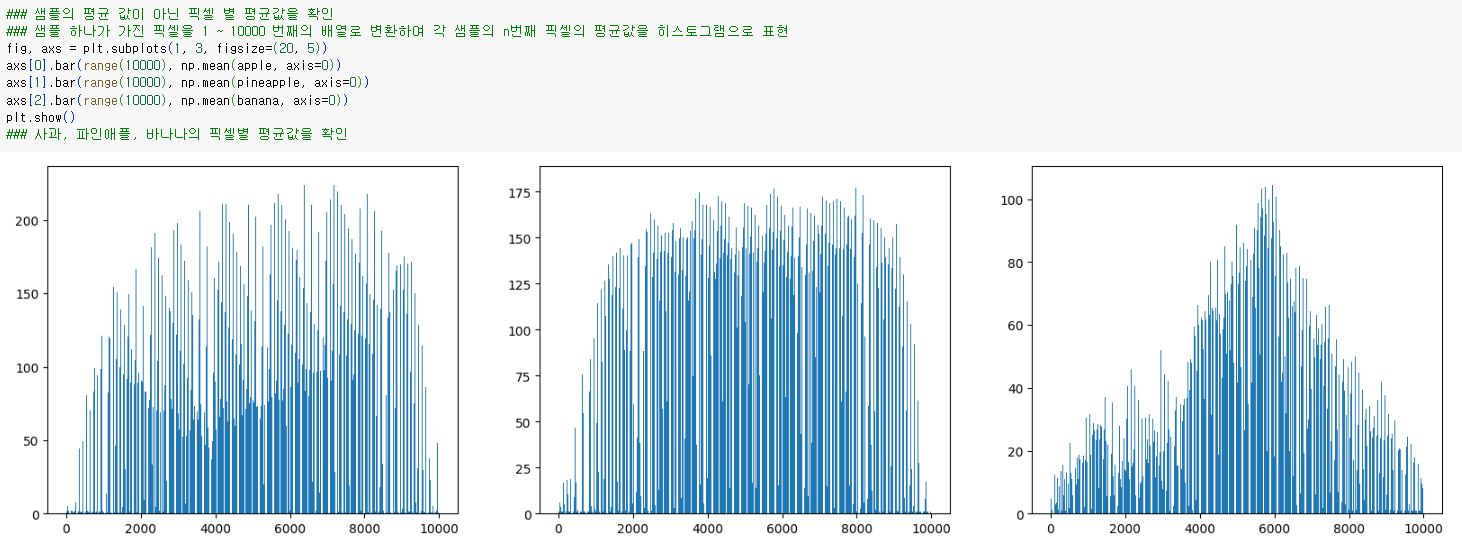
샘플 하나가 가진 픽셀을 1 ~ 10000 번째의 배열로 변환하여 각 샘플의 n번째 픽셀의 평균값을 히스토그램으로 표현
-
사과, 파인애플, 바나나의 픽셀별 평균값을 확인
-
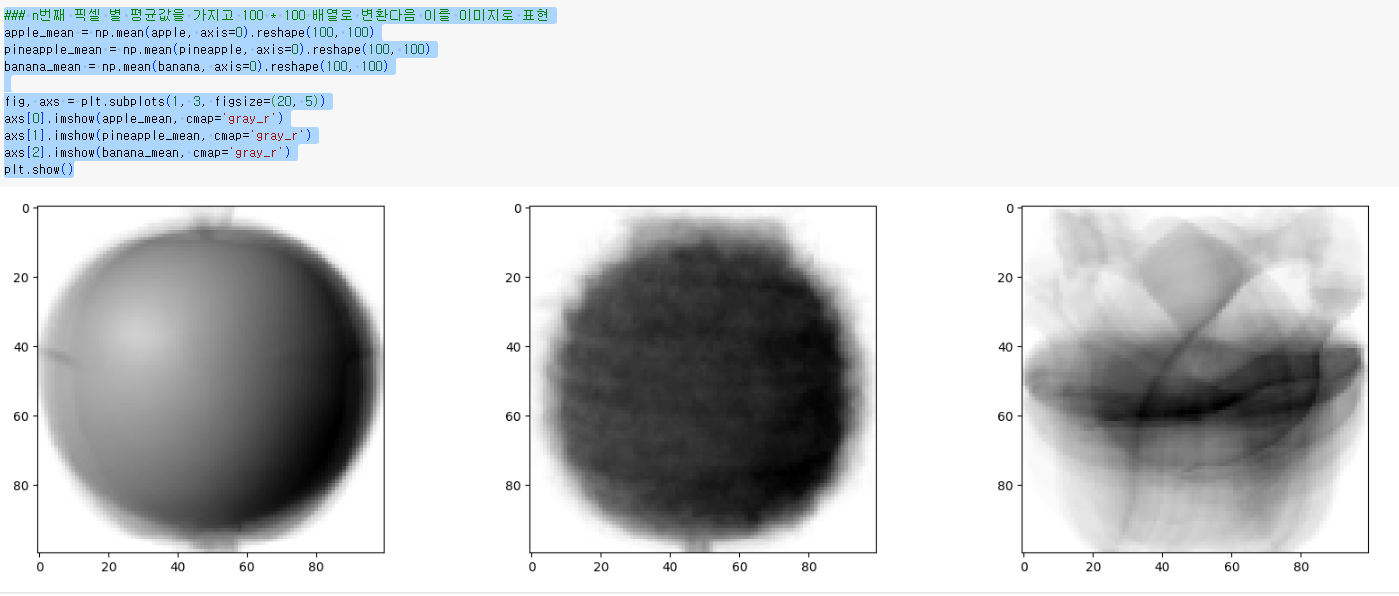
n번째 픽셀 별 평균값을 가지고 100 * 100 배열로 변환다음 이를 이미지로 표현
-
평균값과 가까운 사진 고르기
-
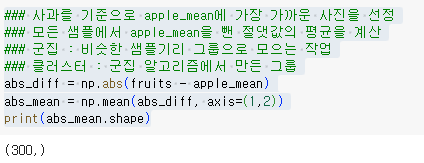
사과를 기준으로 apple_mean에 가장 가까운 사진을 선정
-
모든 샘플에서 apple_mean을 뺀 절댓값의 평균을 계산
-
군집 : 비슷한 샘플기리 그룹으로 모으는 작업
-
클러스터 : 군집 알고리즘에서 만든 그룹
-
평균값에서 가장 오차가 적은 샘플 100개를 순서대로 배치
-
사과 이미지만이 나열된 것을 확인
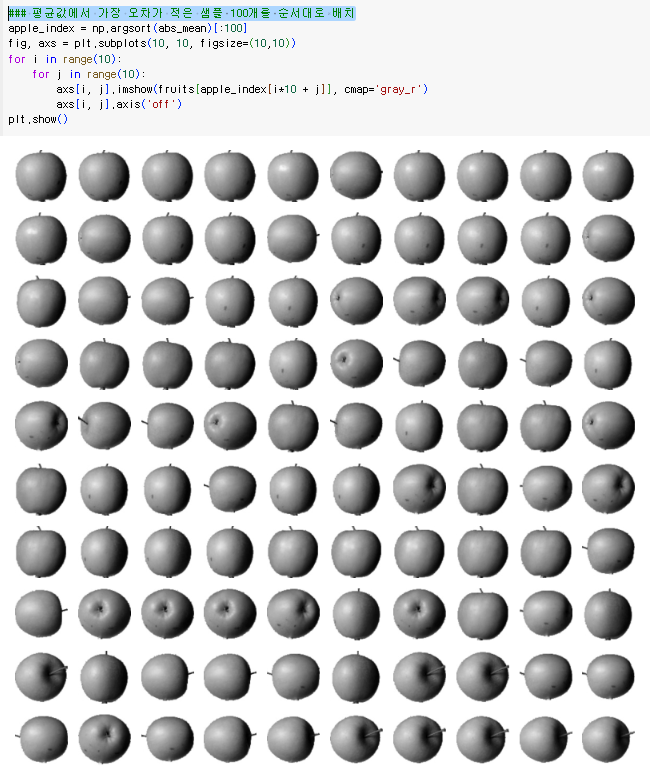
-
axs[i, j].axis('on') 좌표축 표시
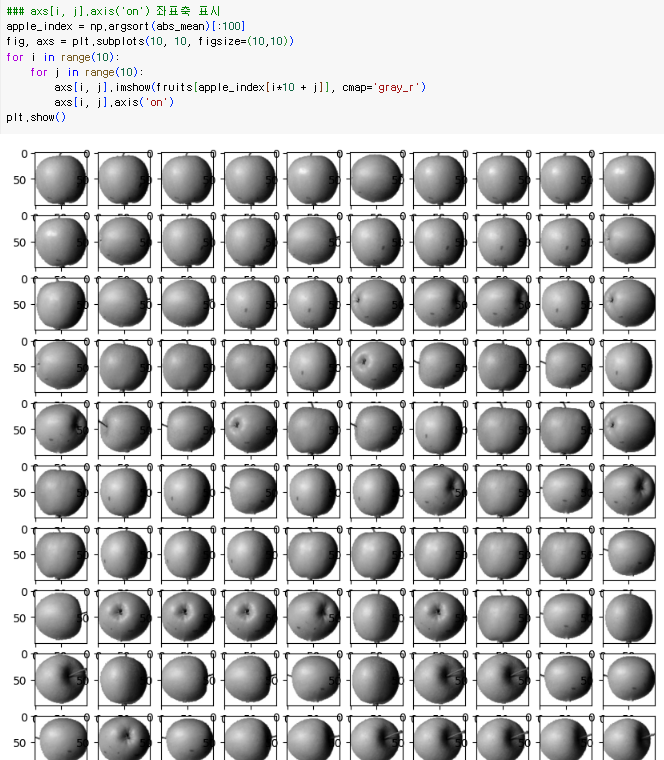
1.1.2. 확인문제

1.2. k-평균
- 타깃값을 알 수 없을 때 사용한다.
- 군집 알고리즘이 평균값을 자동으로 찾는다.
- 클러스터 중심(센트로이드) : 클러스터의 중심에 위치하는 평균값
1.2.1.k-평균 작동 방식
- 무작위로 k개의 클러스터 중심을 정한다
- 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경
- 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복
1.2.2. 실습
-
데이터 수집
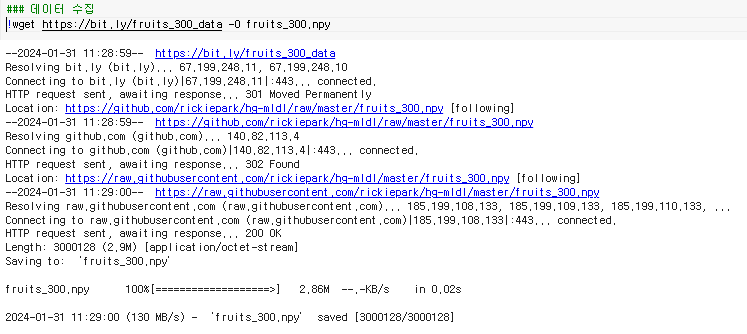
-
샘플 개수, 너비, 높이로 구성된 3차원 배열을 샘플 개수, 너비*높이의 2차원 배열로 변경
-
k-means 클러스터 학습
-
비지도 학습임을 감안하여 타깃 데이터를 사용하지 않음
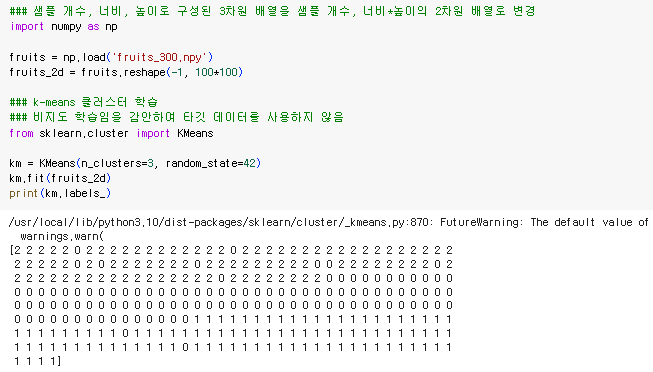
-
세 개의 클러스터로 모인 샘플의 수를 확인

-
각 클러스터에 속한 이미지를 확인하기 위한 함수 생성
-
클러스터 0에 대한 이미지 사진을 출력
-
km.labels==0 : km.labels이 0 인값 외에는 모두 false가 됨
-
불리언 인덱싱 : 불리언 배열을 사용해 원소를 선택하는 방법

-
각 클러스터에 속한 이미지를 확인

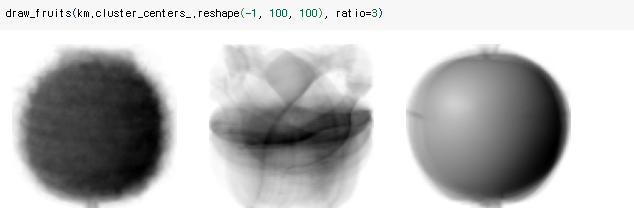
1.2.2.1. 클러스터 중심
-
clustercenters 속성에 저장되어 있음
-
3d를 2d로 변경한 데이터이기 때문에 각 중심을 이미지로 출력하려면 100 * 100 크기의 2차원 배열로 변경 필수
-
transform() : 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환해주는 메서드
-
인덱스가 100인 샘플에 transform() 메서드 적용
-
[[3393.8136117 8837.37750892 5267.70439881]] 이를 통해 인덱스 100 샘플은 클러스터 0에 속할 것이다.

-
가장 가까운 클러스터 중심을 예측 클래스로 출력하는 메서드

-
인덱스 100의 이미지 출력
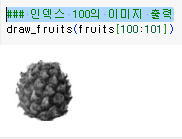
-
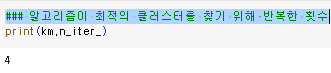
알고리즘이 최적의 클러스터를 찾기 위해 반복한 횟수
1.2.2.2. 최적의 k 찾기
- 비지도 학습은 군집의 개수 조차 모르기 때문에 최적의 군집 수를 결정하는 작업 또한 필요하다
- 엘보우 방법 : 클러스터 개수를 늘려가며 이너셔의 변화를 관찰하여 최적의 클러스터의 수를 찾는 방법
- 이너셔 : 클러스터 중심과 클러스터에 속한 샘플 사이의 거리의 제곱 합
- 클러스터에 속한샘플이 얼마나 가깝게 모였는지를 나타냄
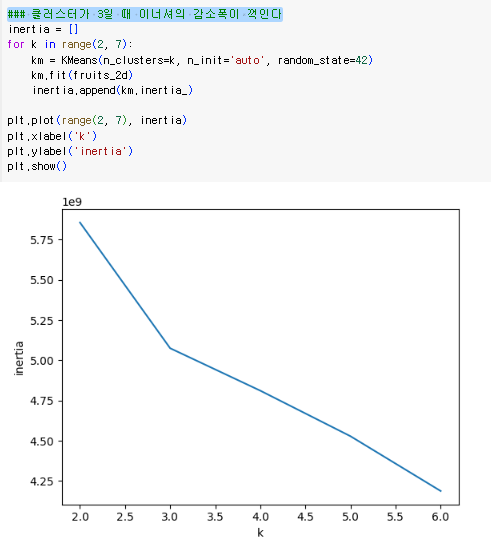
- 클러스터의 수가 증가하면서 이너셔의 감소폭이 꺽이는 지점이 최적의 클러스터 수
- 클러스터가 3일 때 이너셔의 감소폭이 꺽인다
1.3. 차원, 차원 축소
- 차원 : 데이터가 가진 속성
- 과일 사진의 경우 100 100개의 픽셀이 있기 때문에 100 100개의 특성을 가졌다고 볼 수 있다.
- 다차원 배열에서 축의 개수가 차원 -> 2차원 배열에서 행과 열이 차원
- 1차원 배열(백터)의 경우 원소의 개수가 차원
- 차원 축소 : 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능을 향상 시킴
1.3.1. 주성분 분석(Principal Component Analysis - PCA)
-
분산 : 데이터가 퍼져있는 정도
-
주성분 : 데이터가 퍼진 정도를 가장 잘 나타낼 수 있는 선(백터)
-
주성분 백터의 원소 개수 = 원본 데이터셋에 있는 특성 개수
-
원본 데이터는 주성분을 사용해 차원을 감소 가능
-
주성분은 원본 차원과 같고 주성분으로 바꾼 데이터는 차원이 줄어든다
-
특성(또는 차원 또는 컬럼)의 수가 11개 이면 11개의 주성분을 만들 수 있다. 특성 3개 만으로 데이터 분포의 대부분을 보존할 수 있다면 주요 특성 세 가지로 분석하는 것이 주성분 분석이다.
-
첫 번째 주성분을 찾고 이 백터에 수직이며 분산이 가장 큰 방향을 탐색 -> 그 백터가 두 번째 주성분
-
데이터 수집
-
데이터를 100 * 100으로 배열
-
n_components : 매개변수에 주성분의 개수를 지정
-
비지도 학습이므로 fit() 메서드에 타깃값에 미제공

-
배열의 첫 번째 차원=50, 주성분의 개수=50
-
두 번째 차원은 항상 원본 데이터의 특성 개수=10000

-
주성분의 그림을 확인
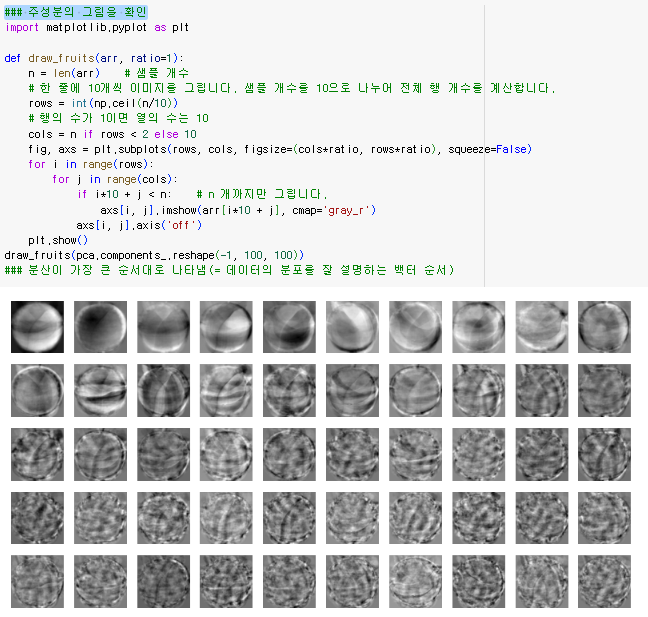
-
원본 데이터의 특성 개수
-
pca.transform() 10000개의 특성을 50개로 축소
-
50개로 축소한 차원을 10000개로 복원
-
복원은 되었으나 원본이미지와 다소 차이가 있다.


1.3.1.1. 설명된 분산
- 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지를 기록
- pca.explainedvariance_ratio : 각 주성분의 설명된 분산 비율을 확인
- 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산 비율을 얻을 수 있음
- 처음 10개의 주성분 대부분의 분산을 표현
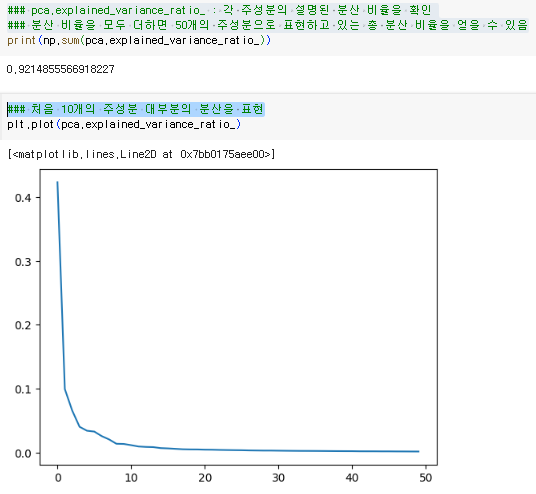
1.3.1.2. 로지스틱 회귀 모형과의 비교
-
로지스틱 회귀 모델의 학습

-
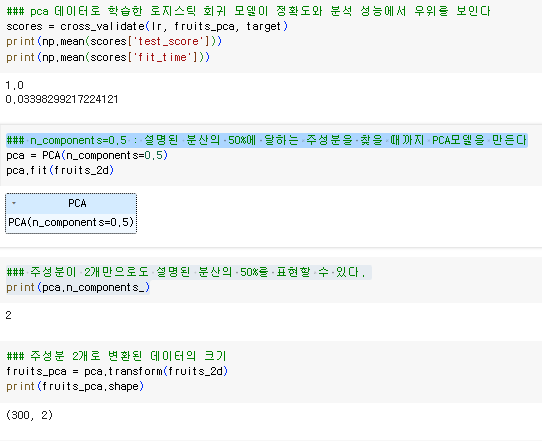
pca 데이터로 학습한 로지스틱 회귀 모델이 정확도와 분석 성능에서 우위를 보인다
-
n_components=0.5 : 설명된 분산의 50%에 달하는 주성분을 찾을 때까지 PCA모델을 만든다
-
주성분이 2개만으로도 설명된 분산의 50%를 표현할 수 있다.
-
주성분 2개로 변환된 데이터의 크기
-
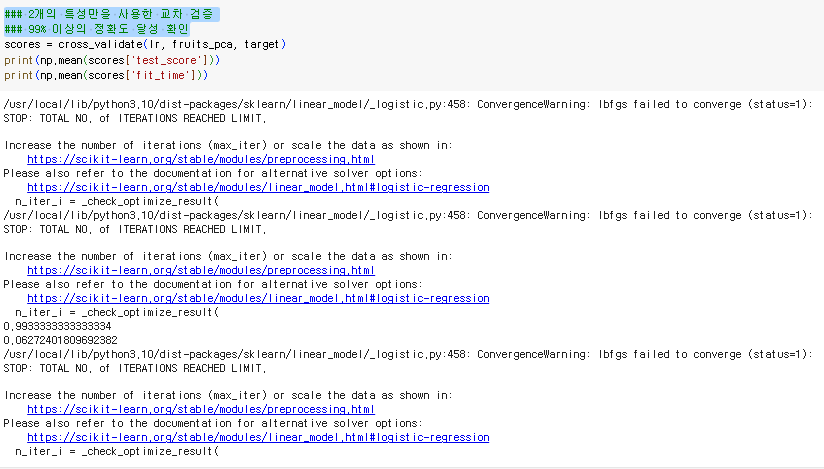
2개의 특성만을 사용한 교차 검증
-
99% 이상의 정확도 달성 확인
-
k-평균 알고리즘으로 클러스터 확인
-
각 클러스터에 속하는 샘플의 수 = 110, 99, 91

-
클러스터 별로 이미지 사진 출력
-
3개이하의 차원으로 줄이면서 샘플의 이미지 출력 시간이 대폭 감소


-
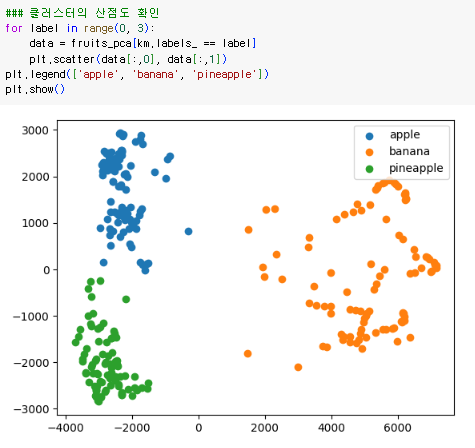
클러스터의 산점도 확인