좌표계 변환
Ax = b에서 I는 b에 숨겨져 있어, Ax = Ib라고 할 때(I는 identity matrix), A는 좌표계고, x와 b는 좌표값이며, I는 표준 좌표계라고 할 수 있다.
여기서 표준 좌표계란, x, y축을 기준으로 Ib일 경우 b가 실제 표준인 x,y축에 대응한 좌표값을 가지고 있는 것이다.
반면에 Ax같은 경우 변환된 좌표계 A에서의 좌표값 x를 나타낸 것이다.
즉 Ax는 Ib를 변환한 것과 마찬가지 이다.
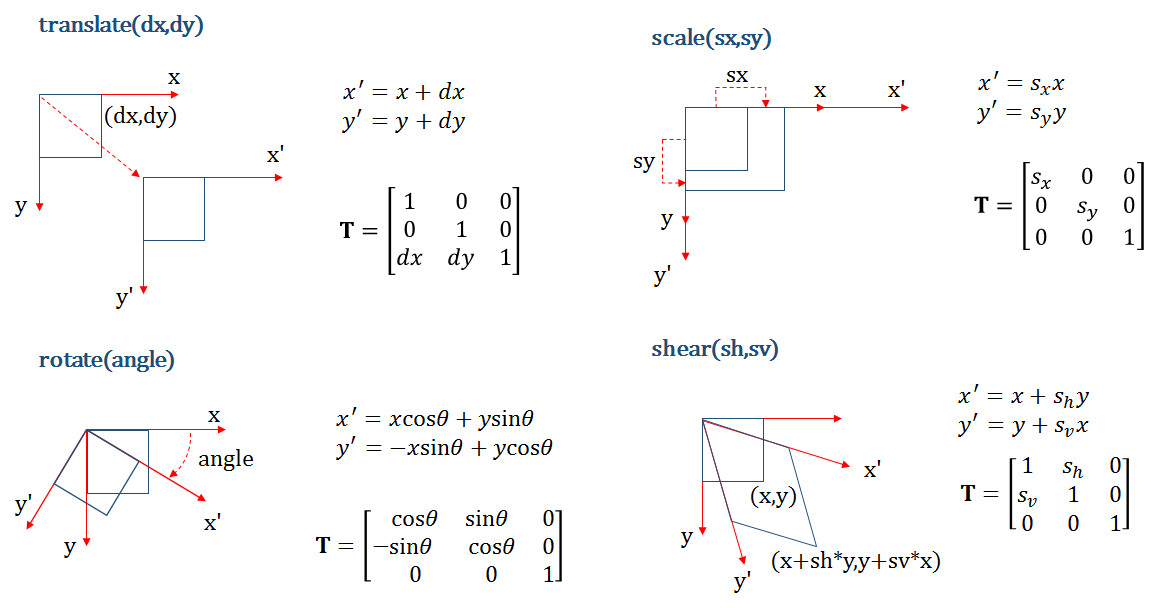
T는 변환된 좌표계를 의미한다. 첫번째 translate를 보면 x, y좌표계가 dx, dy만큼 움직인 것을 알 수 있는데, 이때 가지는 좌표값 x', y'은 dx, dy를 더한 값이라는 것을 알 수 있다.
이 좌표계를 가지는 좌표값을 만약 (x,y) 라고 할 경우 표준 좌표계에서 표현하면, (x+dx, y+dy)이지만 변형된 좌표계에서의 좌표는 (x, y)인 것이다.
좌표계가 달라질 수록 식이 같아져도 좌표계를 바라보는 관점이 달라진다.
Linear Transformation
선형변환은 행렬이 함수와 같다는 의미이다. 이는 인공지능에서 back-propagation, 그리고 convolution layer에 이용된다.
실제 domain을 넣었을 때 codomain이 나오는 것이다.
잠깐 선형함수 정의를 알고 가자. 선형 함수는 이를 그려봣을 때 직선 또는 차원이 3차원이면, 평면 형태를 띄는 함수이다.
이때 선형 함수는 다음과 같은 조건을 만족한다.
f(x+y) = f(x) + f(y)
f(cx) = cf(x)f(x) = 2^x면 이 조건을 충족하지 못할 것이다.
이때 선형변환은 matrix에서 다음과 같은 차원변환을 의미한다.
n차원 vector -> m차원 vector
즉, 어떤 선형 함수를 일으켰더니 다음과 같은 vector의 차원변환이 일어난 것이다.
또한 이러한 행렬 사이의 선형 변환된 함수는 다음과 같은 조건을 만족한다. 행렬 Ta(x) = Ax라고 했을 때,
Ta(x+y) = Ta(x) + Ta(y)
Ta(cx) = cTa(x)먼저 Ta(x+y)인 경우 함수에 들어가기 전인 x+y는 n차원 vector들의 연산이다. 그러나 Ta(x) + Ta(y)같은 경우 m차원 vector들의 연산이다. 이 둘이 같으면 행렬 선형 함수의 조건을 만족하게 되는 것이다.
함수를 만든다는 것은 Ax를 만든다는 의미이므로, A를 제작하는 것이 함수를 만드는 것이라고 볼 수 있다. 따라서, mn standard matrix를 구성하는 것이 함수 구성 방법이다.
xy좌표계를 theta 만큼 회전한다 했을 때 위에서 좌표계를 rotate하는 T matrix는 A가 될 것이고, 이는 선형 함수가 된다.
Ax = b에서 A는 표준 좌표계에서 변형된 좌표계인데, 이는 선형함수를 의미하기도 한다는 것이다. (Ax는 선형조합이니, 선형함수의 조건을 만족한다.)
