출처 : programmers 인공지능 데브코스
행렬 표기법
- row, col, entry
- entry는 각 행렬의 "요소"
- A = [aij]m*n
- mn --transpose--> nm
- if O : zero matrix, A+O = O+A = A O와 A크기 같아야 함.
- nn matrix에서는 aii는 diagonal vector
- Identity Matrix I, IA = AI
- A @ B = C, mr @ rn = mn (모든 집합체의 내적연산을 의미합니다.)
- 행렬곱은 병렬적으로 처리가 가능하여 병렬가속이 가능
- scalar는 1*1짜리 matrix와 같음
- 벡터는 여러 숫자가 일렬로 늘어놓은 구조
- 응용문제에 따라 행부터 읽어들일지, 열부터 읽어들일지 결정함. 근데 보통 열벡터로 쓰임. (선형조합에서 나올 것)
- k-tensor 0 : scalar, 1: vector, 2: matrix
- partitioned matrix
각 행렬을 sub matrix로 고려해도 무방하다.
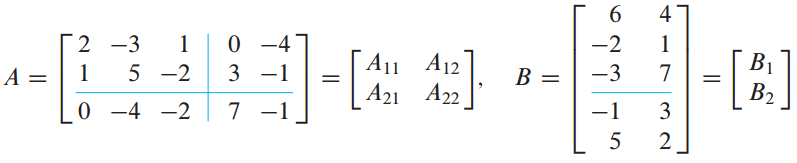
행렬을 블록으로 나눠도 연산후 결과는 같음.
Linear Combination
Ax = b일 때 Ax는 A의 열벡터에 대한 선형 조합으로 말할 수 있다.
선형 조합은 Ax가 행벡터가 되는건데, 각각 A가 가진 행렬의 열벡터가 x에 대응되기 때문이다.
이때 Ax = b에서 A[x1, x2, x3, x4] = [Ax1, Ax2, Ax3, Ax4]처럼 대응이 되게 되고, 이는 x를 가중치라 하였을 때 다음과 같이 표현할 수 있다.
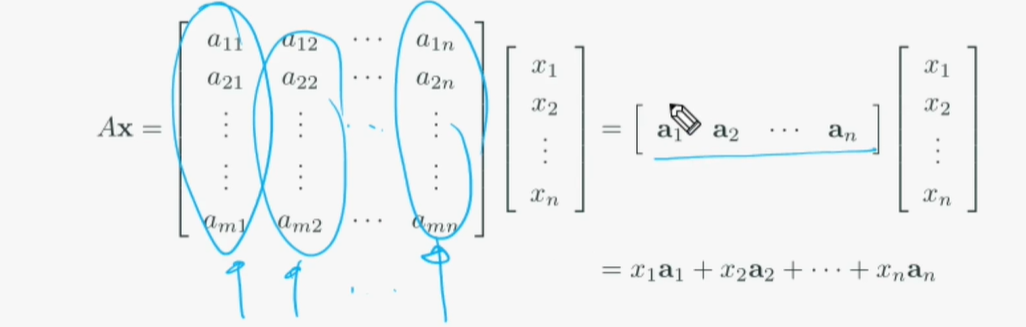
그러면 저 아래의 가중치 합을 선형 조합이라고 한다. (각 내적 값들의 합 @)
선형조합의 관점에서 본다면, A의 가중치 합안에서 해가 발생해야 한다. 그런데, 만약 해가 없다면?(inconsistent) 그러면 가능한 선형조합이 없다고 말한다.
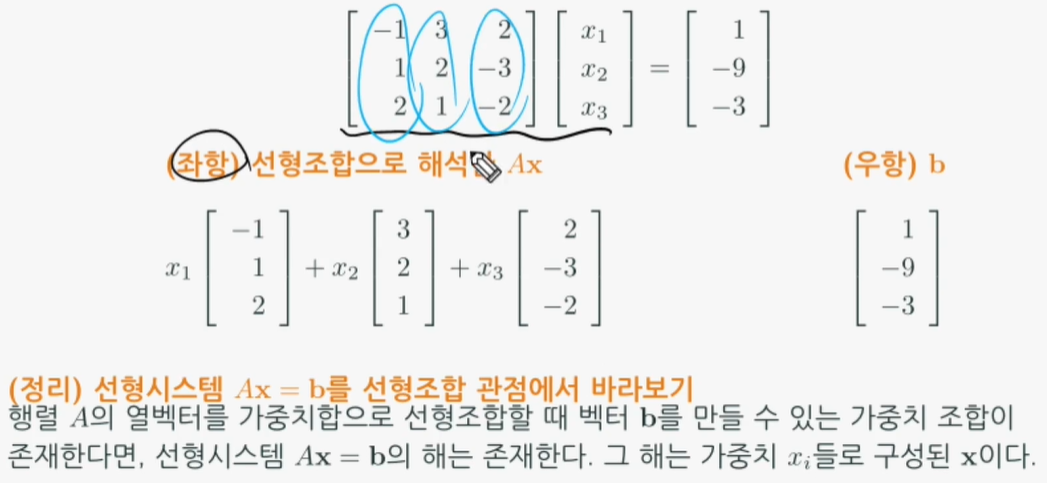
아래의 정리를 보자. 선형 조합이라는 것은 (좌항)으로 표시된 Ax를 의미하게 된다.
