참고자료1 참고자료2 참고자료3 참고자료4

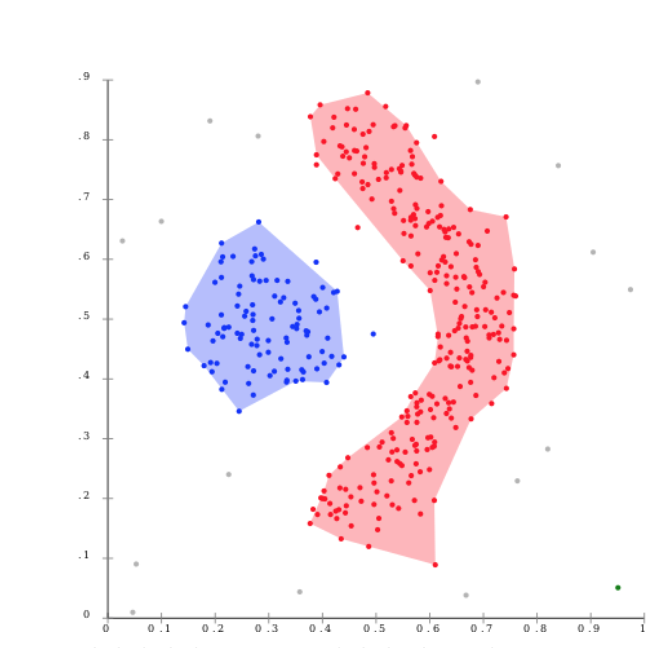
지도학습

지도학습은 앞에서 말했듯이 이미 이전 데이터가 존재한 상태에서 새로운 입력 데이터가 들어갔을 때 결과 값을 만들어 낸다.
즉 이전에 있던 데이터 셋을 참고해서 그 다음 들어올 데이터 셋의 결과(분류, 회귀후의 결과)를 결정한다고 생각하면 된다.

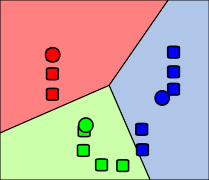
우리는 이를 파악할 때 해당 데이터 셋들의 특징을 가로, 세로축에 놓은 후 이미 존재하는 데이터 셋을 뿌려 놓은 후, 새로운 데이터가 들어왔을 때 그 데이터가 어디 class에 포함되는 지를 알아볼 것이다.

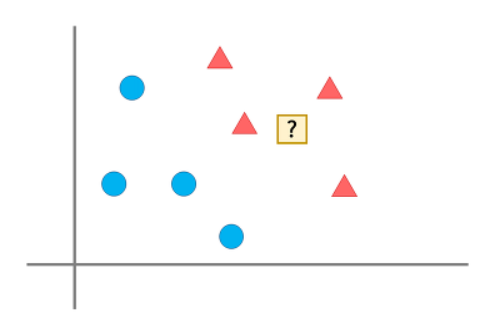
이런 그림 속에서 ?가 세모에 속하는지 네모에 속하는지를 알아보는 것이다.

1. k-최근접 이웃

k-최근접 이웃은 일단 먼저 데이터 셋을 불러온 후, 새로운 데이터가 들어왔을 때 그 데이터를 가장 가까운 데이터와 연결시켜주는 것을 말한다. k는 이때 연결할 가까운 이웃의 개수를 의미한다.

이웃이 많아지면 주변에 어떤 이웃이 있는지 파악하고 어떤 class의 이웃이 가장 많이 존재하는지 파악한 후 그 class를 새로운 데이터 셋의 class로 지정하게 되는 것이다.

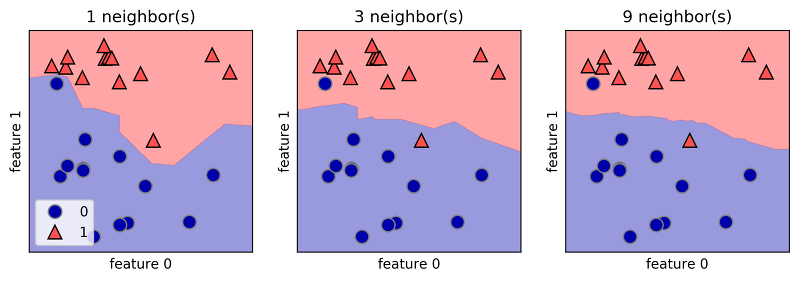
따라서 k가 높아질 수록 위와 같이 점점 결정 경계 (decision boundary)가 부드러워 지는 것을 알 수 있다.

이때 결정 경계는 알고리즘이 각각의 class로 나누게 되는 경계이다.

결정 경계가 부드러워진다는 말이 알고리즘의 정확도를 높인다는 말로 오해할 수 있는데, k의 값은 데이터 마다 다르기 때문에 최적의 k값을 찾아야 한다. 다음 그래프를 보자.

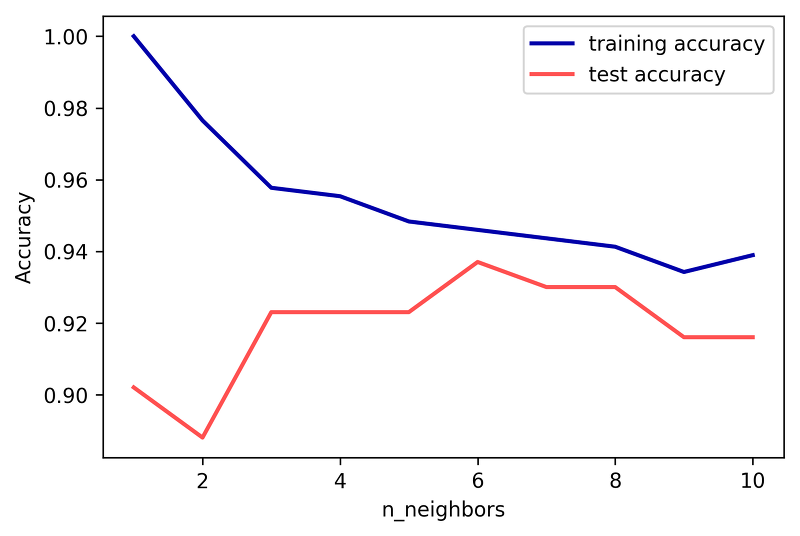
우리는 일단 test data의 accuracy가 높아야 한다는 것을 기억하자. test 데이터가 새로 들어온 데이터이고 train 데이터가 이전의 데이터를 의미하기 때문이다.

이때 k값이 작으면 훈련 데이터의 정확도는 높을 것이다. 왜냐하면 k값이 작을 수록 훈련데이터에만 적절하도록 훈련이 되기 때문이다.
그러나, test 데이터의 정확도는 낮다. 새로 들어온 데이터는 결정 경계가 너무 들쑥날쑥하기 때문에 일반적으로 class 1의 특징을 가진 것이 class 0으로 오인할 수 있기 때문이다.
test accuracy가 떨어짐

k값이 너무 높아도 문제다. 그런 경우에는 오히려 test 데이터에서 class 1 데이터 셋의 특징과 비슷하지만 class 0인 데이터가 들어왔을 경우 class 1로 금방 판단해 버릴 가능성이 점점 심해지기 때문이다.
test, train accuracy가 둘 다 떨어짐

그래서 전자를 과대적합(Overfitting), 후자를 과소적합(Underfitting)이라 한다.

위는 분류의 예시인데, 만약 회귀일 경우에는 다음과 같이 그래프가 나온다고 한다.

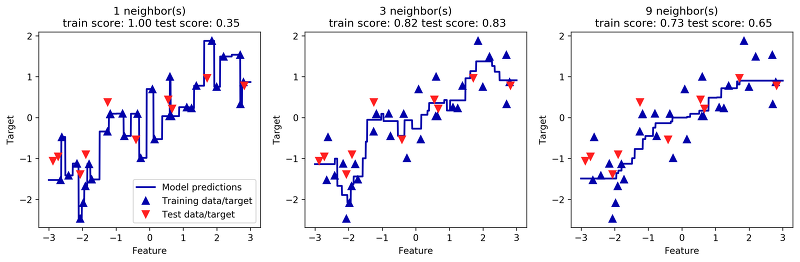
Target은 나온 결과 값이고 파란 점은 training data, 빨간 색은 test data다. 분류와 마찬가지의 결과가 나온다는 것을 알 수 있다.

2. 나이브 베이즈

각각의 class를 고려하여 분류하는 지도학습 알고리즘의 일종으로, 다음과 같은 베이즈(정리)공식을 기본으로 한다.

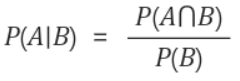
이는 B가 일어난 경우에서 A의 확률을 나타낸 것이다. 이 확률을 구하려면 A와 B가 동시에 일어날 확률과 B가 일어날 확률을 알아야 할 것이다.

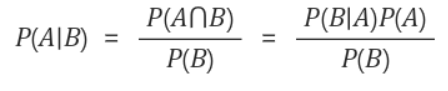
식이 이런경우에는 A가 일어난 경우에서 B가 일어날 확률과 A, B의 확률을 각각 구하면 된다.

이러한 공식을 이용해서 주어진 경우의 확률을 계산할 수 있게 되는 것이다. 결국 A,B등의 요소는 해당 데이터 셋의 특징이 될 것이고, 확률은 이전 데이터 셋에 의해서 정의된다.

따라서 정의된 확률에 의해서 새로운 데이터는 class를 정하게 될 것이다.

나이브 베이즈는 가우시안, 다항분포, 베르누이 나이브 베이즈로 종류가 세가지인데, 이는 아래를 참고하길 바란다.

참고로 예시에서 여성과 남성을 구분하는 부분에서는 가우시안 나이브 베이즈를 이용하였고(매개변수를 정의함) 스팸메일 같은 경우 두 가지 class로 나눠지기 때문에 베르누이 나이브 베이즈를 이용하였다.

나이브 베이즈 위키

3. 의사결정트리

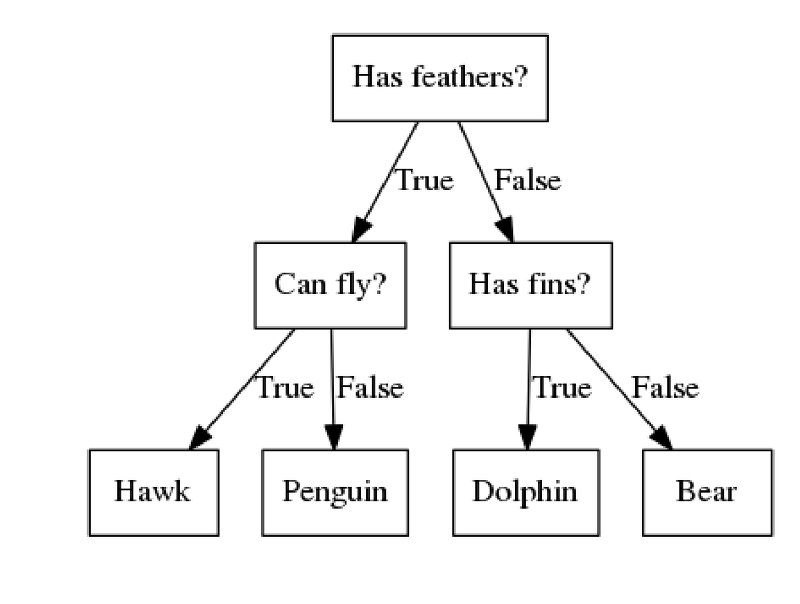
우리가 일반적으로 아는 tree 구조와 같다. 데이터를 질문을 통해서 분류하는 방법으로 각 질문들은 leaf가 되고 leaf들을 따라서 node를 분류하여 class를 정해주는 방법인 것이다.

이때 만약 분류로 할 경우에는 하나의 class를 가질 때 까지 질문을 거치고, 회귀와 같은 경우 하나의 분석결과를 가질 때 까지 질문을 하게 된다.

위의 그림을 보면 질문의 깊이가 깊어질 수록 점점 더 훈련 데이터를 정확하게 나누는 것을 알 수 있다.

또한 이러한 질문들에는 특성 중요도가 있다. 0과 1사이로 가정되는데, 질문을 많이 거쳐갈 수록 1에 가까워지고 질문을 거쳐가지 않을 수록 0에 가까워 진다. 이를 이용하여 중요한 질문을 보기 쉽게 정리할 수 있다.

그렇다면 최적화된 결과를 내기 위해서는 어떻게 해야할 것인가?

트리 알고리즘이 KNN과 비슷한 점은 의사결정트리는 depth가 높아질 수록 training data의 정확도가 높아지지만 test data의 정확도는 낮아지는 Overfitting이 일어난다는 점이다. (물론 KNN에서는 k가 작을 수록 이 현상이 심해졌다)

이를 해결하기 위해서 나온 것이 트리 생성을 일찍 중단하는 사전 가지치기 (pre-pruning), 두번째는 트리를 전부 만든 뒤에 데이터 포인트(특성 중요도로 해석함) 가 낮은 leaf를 삭제하는 사후 가지치기 (post-pruning)이 있다.

이때 의사결정트리에 지도학습의 회귀모델을 적용하는 부분에서 궁금한 부분이 있다.
만약 들어오는 데이터가 훈련된 모든 질문들에 해당하지 않는 그런 범위외의 데이터라면 어떻게 될까? 그러면 target(결과값)을 정의할 수 없지 않을까?

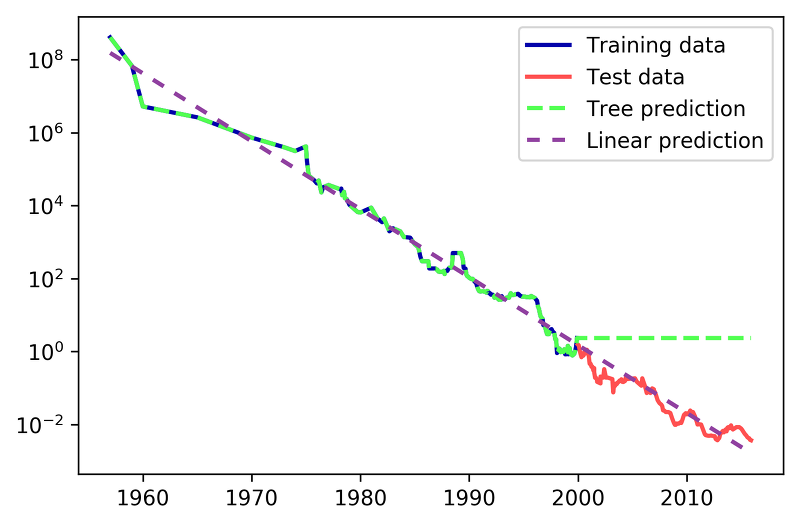
위는 RAM의 가격을 예측한 그래프이다. RAM가격은 2000년 이후로 계속 가격이 싸졌는데, 선형 회귀 모델 같은 경우 새로운 데이터를 예측하였지만 tree는 하지 못했다. 이는 tree의 질문 범위 밖의 data이기 때문이다.

이를 해결하기 위해 결정트리 앙상블이 만들어지게 되었다.

비지도학습

비지도 학습은 전에 말했듯이 이전의 데이터가 존재하지 않아서 새로운 데이터의 패턴과 관계를 찾아내는 것이라고 하였다. 따라서 여기에서의 알고리즘은 주로 이 데이터들이 어떠한 특성에 인과관계를 가지는 지 혹은 어떤 특성을 기준으로 데이터 셋을 나눌 것인지에 초점이 맞춰져 있다.

또한 우리는 비지도 학습의 종류에는 변환, 연관규칙, 군집화가 있다고 했다. 다음 알고리즘들을 보자.

1. PCA

PCA(Principal component analysis)는 변환 모델의 알고리즘 중 하나로, 데이터 셋의 특성을 머신이 알기 쉽게 데이터를 변환하는 것이라고 했다.

따라서 주성분 분석같은 경우 실제 데이터 셋을 특성에 따라 표시한 후 그 데이터 속에서 중요한 성분을 찾아내게 된다.

아래 그림을 보면 먼저 component 1이라는 주요성분을 찾아내게 되는데, 이는 분산의 가장 큰 방향으로 정해지게 된다. 또한 우리는 component 1과 직교하는 component 2를 찾게 되고, 그림과 같은 2차원 배열이면 하나밖에 존재하지 않겠지만 만약 특성이 여러 개일 경우에는 직교하는 축이 많을 것이다. 그 축 중에서 또 가장 분산 값이 큰 축을 component 2로 정의하는 것이다.

그래서 이 두 축을 이용하여 우측 그림과 같은 모양의 그래프를 나타낼 수 있다.

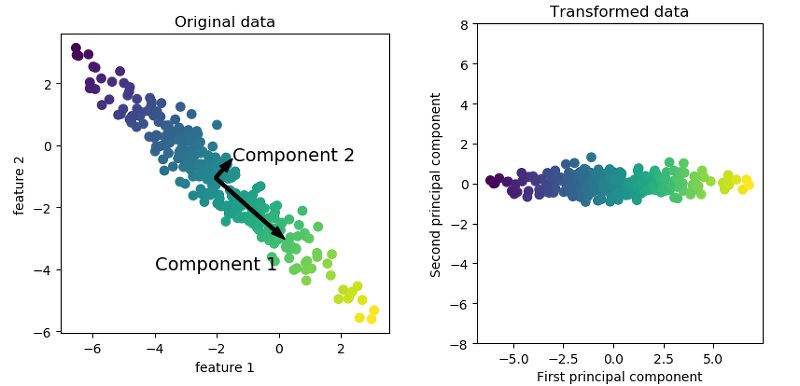
이런 식으로 데이터를 나타내면, 먼저 데이터의 평균값은 모두 0으로 수렴하게 되며, 데이터의 범위를 재 조정하므로써 중요 차원(특성)만 골라서 그래프를 그려낼 수 있다.

또한 우리는 PCA를 통해 차원 축소를 할 수 있는데, 이는 PCA를 통해 중요한 특성을 골라줄 뿐만 아니라 중요하지 않은 특성은 버려서 최적화된 데이터 셋으로 변환시킬 수 있다는 것을 의미한다. 아래 그림을 보자.

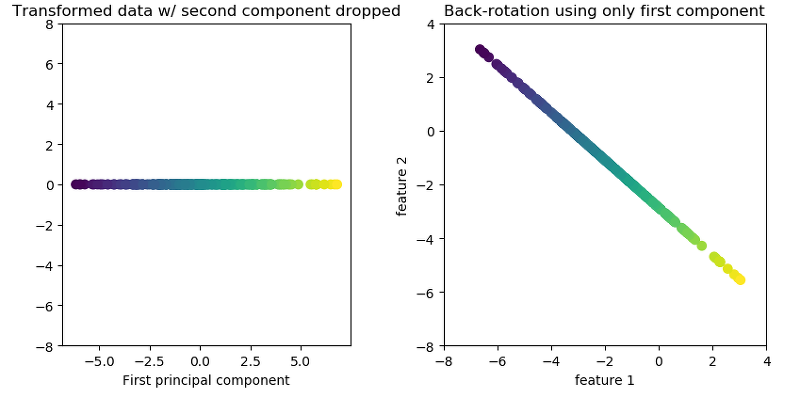
이 그래프는 위에서 언급했던 2차원의 그래프를 1차원으로 줄인 것을 말한다. component 2를 기준으로 퍼져있었던 데이터가 1차원, 즉 직선으로 만들어지면서 component 1에만 데이터가 분류되게 되었다. 우측은 이를 다시 원래 존재하던 특성 1,2의 그래프에 맞춰 그려진 그래프다.

이를 이용해서 데이터의 노이즈 같은 것들을 없앨 수 있게 되는 것이다.

그러면 주성분은 어떤 방식으로 찾을 수 있을까? 여기에서 공분산 행렬이 들어가게 된다.

2차원일 경우 즉 x,y를 특성 1,2라고 가정했을 때, 다음과 같이 (1,1)에는 x의 분산, (1,2), (2,1)에는 x,y의 공분산, (2,2)에는 y의 분산이 들어가게 된다.

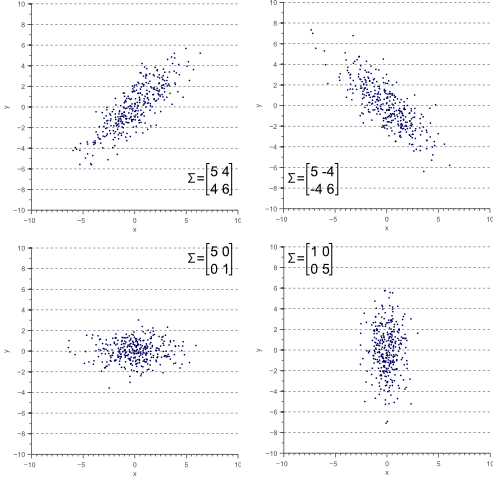
이를 보면 x의 분산이 클 경우 그래프는 가로로, y의 분산이 클 경우 세로로 그래프가 그려지는 것을 볼 수 있고 공분산이 0일 경우에는 수평,수직으로 공분산이 존재할 경우에는 기울기가 생기는 것을 알 수 있다.

따라서 이 공분산 행렬의 eigenvector(고유 벡터)는 이 그래프의 분산 방향이므로, 주성분의 방향을 의미하게 되고, eigenvalue(고유 값)은 분산의 크기이므로, 주성분을 정하는 크기라고 볼 수 있다.

우리는 이것을 얼굴인식에서 응용한 바가 있다.
출처

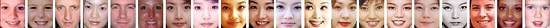
첫번째 그림은 비교할 얼굴들을 학습시킬 모델을 의미하고, 두번째 그림은 학습 시킨 모델들의 주 성분을 추출해 낸 얼굴이며 왼쪽으로 갈 수록 분산 값이 크기 때문에 맨 왼쪽의 주성분 추출이 가장 큰 분산 값을 가지게 된다.

분산 값이 작을 수록 노이즈가 심해진다는 것을 알 수 있었다. 두번째 그림은 원래 45*40(그림의 크기) = 1800차원의 특성을 가진(pixel단위로 특성이 생성되기 때문) 것인데, 분산이 큰 20차원으로 축소해서 가져온 것이다.

이를 이용해서 주성분으로 근사한 이미지들(차원 축소한)은 다음과 같다. k의 값은 고려한 주성분의 개수이다.

차원이 감소할 수록 거의 같은 얼굴을 보이고 있는데, 이는 주성분이 감소하기 때문에 각 얼굴들의 고유한 특성을 살리기 힘들기 때문이라고 해석할 수 있다.

2. k-means(k-평균군집)

비지도학습 군집 모델의 알고리즘 중에서 가장 간단한 방법으로, 이는 군집의 특성상 k개의 군집을 형성하는 것이 주 목적이다.

같은 클러스터의 내부 데이터 유사성을 점점 증가시키는 방향으로 군집을 형성한다.

다음 그림을 보면 쉽게 파악할 수 있다.

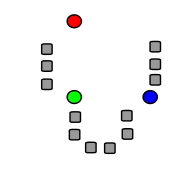
1. 먼저 k개의 데이터 포인트를 무작위로 지정하여, (색깔이 있는 것이 무작위로 선정된 데이터 포인트임) 해당 데이터 포인트가 클러스터의 중심이 된다.

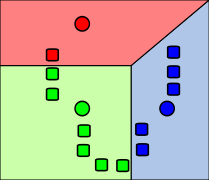
2. 각 데이터들은 선정된 데이터 포인트(클러스터의 중심)중 자신과 가장 가까운 데이터 포인트의 클러스터에 포함되게 된다.

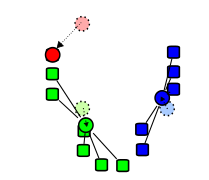
3. 각각의 클러스터들 안에 포함되어 있는 데이터의 평균값을 구하여 그 평균값이 클러스터의 중심으로 다시 바뀌게 된다.

4. 2,3 번과정을 반복하여, 만약 클러스터의 중심이 더이상 움직이지 않을 경우 종료한다.

위와같은 방식으로 유사한 데이터들의 군집을 생성하게 된다.

여기서 분류와 다른 점을 찾을 수 있다. 군집을 만드는 경우에는 단순히 데이터의 묶음일 뿐, 자체적인 의미는 없다는 점이다. 분류는 데이터를 분류할 때 의미있는 어떤 것으로 분류한다는 점에서 군집과 다르다.

주의 사항중 하나는 원래 저 위에서는 무작위로 처음에 초기화를 한다고 하지만 클러스터 중심의 초기화 기법에는 여러가지가 있다. 이는 위키를 참고하기 바란다.

k-means 알고리즘은 위와 같이 단순한 진행으로 이루어 지게 된다는 점에서 많이 이용되고 있다. (나중에 이와 관련된 문제 하나를 알아볼 것이다.)

그러나 역시 k-means 에는 여러가지 문제점이 있다.

첫번째로 실제로 존재하는 군집과 k의 값에 차이가 있을 경우 잘못된 군집을 형성하게 된다.

위와 같은 경우에는 실제로 존재하는 군집은 4개지만 k값을 3개로 설정했을 때 일어나는 현상이다.

또한 k값을 더 크게 했을 경우에는 아래 그림과 같다.

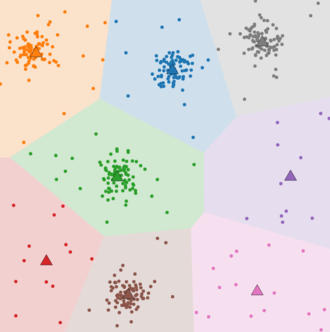
실제로 존재하는 군집은 5개지만 k=8로 했을 경우 나타나는 문제점이다.

또한 다음과 같이 이상점(특이점, 같은 클러스터로 포함해야 하는데, 특성이 군집과 너무 다른 경우)이 존재할 경우에는 대처하기가 힘들다.

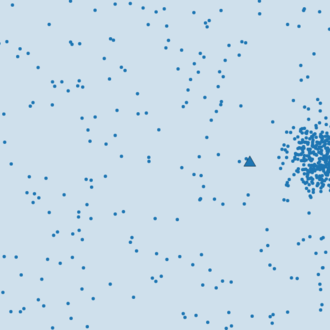
중심점이 클러스터와 많이 떨어져 있는 것을 알 수 있다.

또한 구형 데이터(데이터가 원처럼 존재해 있는경우)와 같은 복잡하고 기하학적인 데이터 셋에서는 군집 형성이 매우 어렵다는 단점도 존재한다.

3. DBSCAN

이 알고리즘 또한 비지도 학습의 군집 모델에 해당하는 알고리즘으로 군집은 가까운 데이터들 끼리 군집을 형성하는 것에 목표를 둔다고 했다.

그러나 이는 k-means와 다르게 데이터의 밀도를 통해서 군집을 형성하게 된다. k-means는 클러스터 중심과 데이터 사이의 거리에 따라 형성되는 것이다.

데이터의 밀도는 두 개의 변수를 통해서 정하게 되는데, 최소 샘플 개수(min_samples)와 지정 거리(eps)이다.

최소 샘플 개수는 어떤 데이터 하나가 있다고 치면 그 데이터의 지정거리안에 몇 개의 데이터가 포함되어야 군집으로 인정되는지를 의미하는 변수이다. 그렇게 되면 지정거리는 군집이 되는 core point를 만드는 최소 단위의 거리라고 볼 수 있다.

DBSCAN에서 데이터는 특성에 따라 각각 3가지로 나뉠 수 있는데, core point, border point, noise point이다.

예시를 보기 전에 최소 샘플 개수(min-samples)는 4개로 지정하고, 지정거리는 아래의 그림과 같다고 정하겠다.

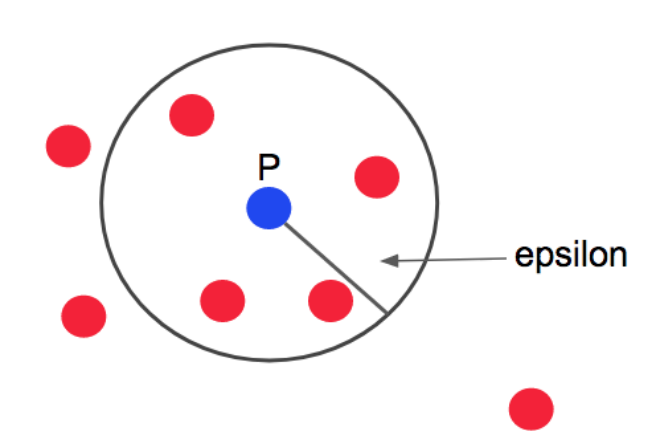
• 위 그림의 경우 P는 지정거리안에 P를 포함해서 총 5개의 점을 가지고 있으므로 core point가 된다.
  epsilon은 지정거리를 의미한다.

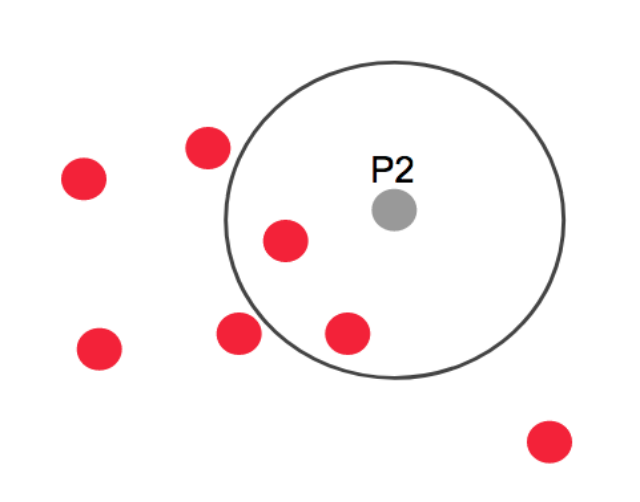
• 이때 같은 그림에서 데이터 P2 같은 경우 지정거리(eps라고 하겠다) 내에 총 3개의 점이 존재하므로, core point가 되지 못한다. 그래도 P의 core point eps안에 존재하는 점이므로, 이 점은 경계점(border point)가 된다.

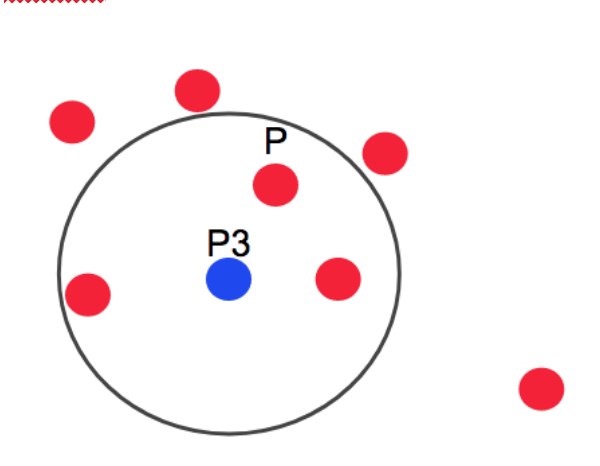
• 같은 그림에서 데이터 P3는 P, P3를 포함해서 총 4개의 샘플 데이터를 가지므로 core point가 되야 한다. 근데 이때 P 또한 core point이므로 이 두 point는 하나의 군집으로 묶이게 되고, 각각의 core point에 포함되는 데이터 들도 하나의 군집으로 묶이게 된다.
  
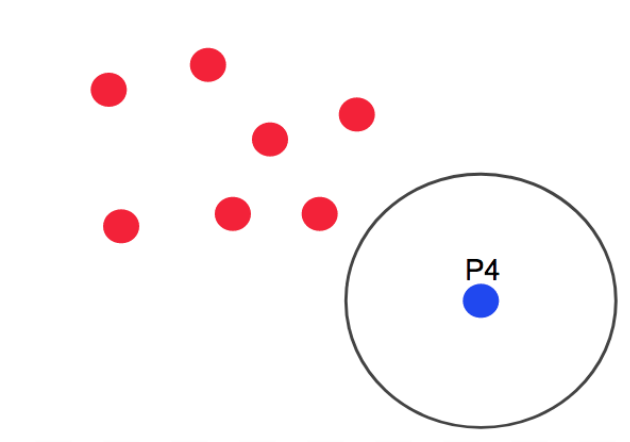
• 위 그림은 떨어져 있는 데이터 P4의 모습인데, 이는 아무런 core point에 섞이지 않았을 뿐더러 eps안에 최소 샘플 개수 만큼의 점이 존재하지 않기 때문에, noise point가 된다.

이를 모두 합하면 다음과 같은 그림이 된다.

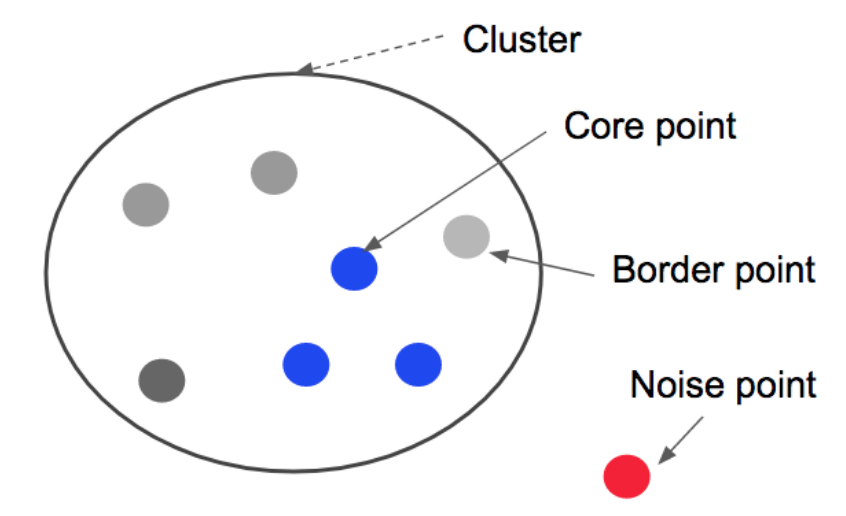
그러면 DBSCAN의 장점은 무엇일까?

• k-means는 기하학적인 모양의 데이터를 관리할 때 군집을 형성하기 어렵다고 했다. 그러나 DBSCAN의 경우 데이터의 밀도를 중심으로 보기 때문에, 기하학적 모양의 군집 또한 설정이 가능하다.
• 이상점이 존재하면 noise point로 분류하기 때문에 이상점 때문에 군집에 문제가 생길 일은 없게 된다.