프로그래머스 자물쇠와 열쇠 [2022 KAKAO BLIND RECRUITMENT]
https://programmers.co.kr/learn/courses/30/lessons/60059
설마 완전탐색일까, 하는 생각으로 오래 고민했지만 결국 완전탐색이 답이었다.
다만 대세에 가까운 풀이 방식과 약간의 차이가 있어 해설을 작성하게 되었다.
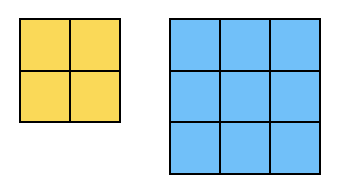
노란색을 key, 파란색을 lock 배열이라고 하자.
많은 경우 key에 위, 아래, 양 옆으로 lock의 length만큼 패딩을 걸고, lock 배열을 움직이며 비교 연산을 수행하셨다.
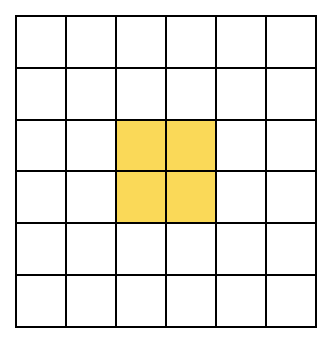
이렇게 패딩을 걸고,
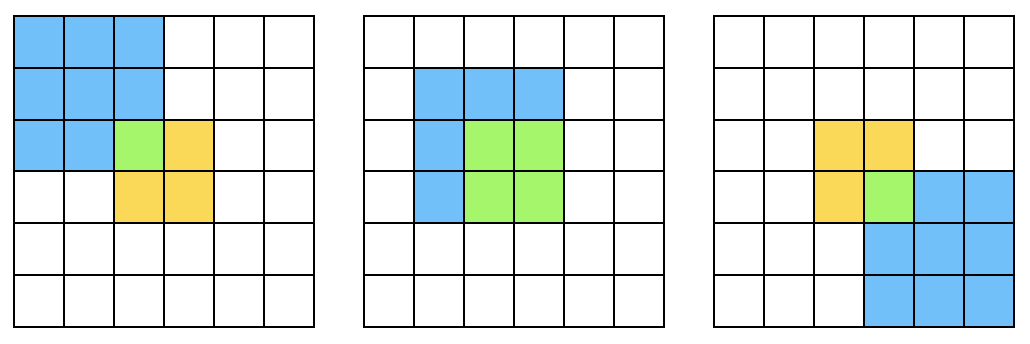
이렇게 움직이며 비교하는 것이다.
이 방법의 장점은
- 비교 시 edge값인지 확인하는 과정을 거치지 않아도 된다.
- 자물쇠가 열쇠와 겹치지 않는 부분에 남은 홈이 있는 지 별도로 확인하지 않아 된다.
간단히 말해, 예외 처리에 비교적 자유로운 편이다.
러프하게 4×(n+m-1)^2×n^2 번의 비교연산을 수행해야 한다.
(n = 자물쇠 배열의 길이, m = 열쇠 배열의 길이)
나의 경우 lock을 그대로 두고, key를 움직이며 비교 연산을 수행했다. 자물쇠와 열쇠가 겹치는 범위에서 문제가 생기지 않는다면, 열쇠가 해결한 홈의 개수와 자물쇠 전체의 홈의 개수를 비교한다. 이 개수가 같을 때만 true를 리턴한다.
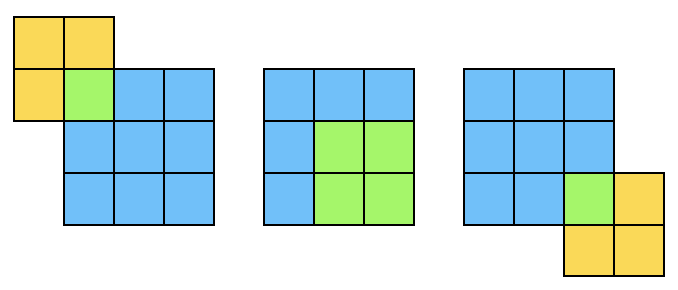
이 방법은 4×(n+m-1)^2×m^2번의 비교연산을 수행해야 한다.
사실 M과 N의 범위가 같으므로 시간복잡도를 묻는다면 두 방법 모두 동일하다.
다만, M이 N보다 작거나 같고, 패딩을 넣기 위해 배열을 카피하는 과정 등이 생략되므로 많은 케이스에서 수행시간이 2~3배 단축 된 것을 확인할 수 있었다.
class Solution {
public boolean solution(int[][] key, int[][] lock) {
int m = key.length, n = lock.length, lockCount = countLock(n, lock);
if(lockCount == 0) return true;
for(int k = 0 ; k < 4 ; k++){
if(k > 0) key = rotate(m, key);
if(bruteForce(m, n, key, lock, lockCount)) return true;
}
return false;
}
public int countLock(int n, int[][] lock){
int lockCount = 0;
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < n ; j++){
if(lock[i][j] == 0) lockCount++;
}
}
return lockCount;
}
public boolean bruteForce(int m, int n, int[][] key, int[][] lock, int lockCount){
for(int i = 1-m ; i < n ; i++){
for(int j = 1-m ; j < n ; j++){
if(find(i, j, m, n, key, lock, lockCount)) return true;
}
}
return false;
}
public boolean find(int x, int y, int m, int n, int[][] key, int[][] lock, int lockCount){
int setCount = 0;
for(int i = 0 ; i < m ; i++){
for(int j = 0 ; j < m ; j++){
int tmpX = x+i, tmpY = y+j;
if(isValid(tmpX, tmpY, n)){
if(key[i][j] == lock[tmpX][tmpY]) return false;
if(lock[tmpX][tmpY] == 0) setCount++;
}
}
}
return setCount == lockCount ? true : false;
}
public boolean isValid(int x, int y, int n){
if(x < 0 || x >= n || y < 0 || y >= n) return false;
return true;
}
public int[][] rotate(int m, int[][] key){
int[][] newKey = new int[m][m];
for(int i = 0 ; i < m ; i++)
for(int j = 0 ; j < m ; j++)
newKey[i][j] = key[m-1-j][i];
return newKey;
}
}