[프로그래머스/Java] 72413번 합승 택시 요금

프로그래머스 합승 택시 요금 [2021 KAKAO BLIND RECRUITMENT]
https://programmers.co.kr/learn/courses/30/lessons/72413

문제를 요약하면 다음과 같다.

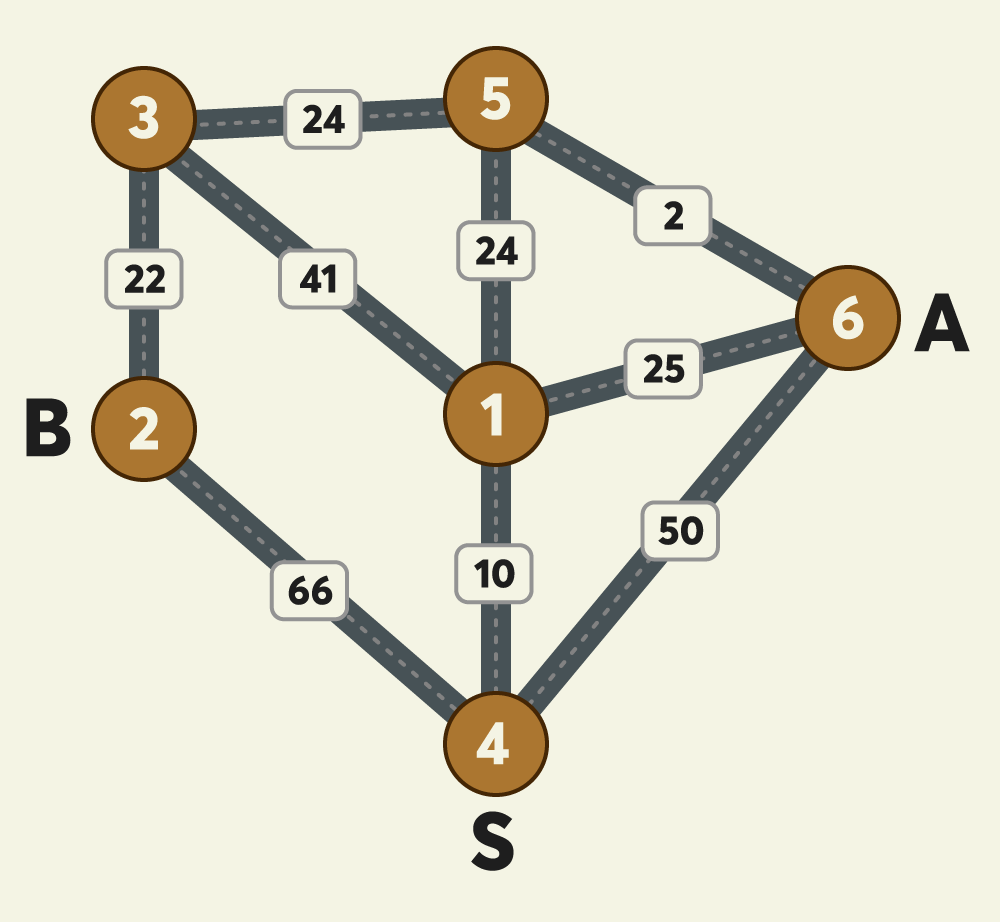
'S에서 X까지 가는 최소 요금 + X에서 A까지 가는 최소 요금 + X에서 B까지 가는 최소 요금'이 최소가 되는 X를 찾아 이 요금을 계산하여라.

여기서 X는 A와 B가 각자의 길을 가게 되는 지점일 것이다.

최소가 되는 X를 찾아야 하기 때문에, X에 1부터 n까지 모두 대입해보아야 한다.
X에서 Y로 가는 최소비용과 Y에서 X로 가는 최소비용이 동일하다는 것도 잊지 말자.

따라서 S, A, B에서 각 정점까지 가는 데 드는 최소 비용을 모두 구해야 하고,
결국 임의의 정점 Y에서 각 정점까지 가는 데 드는 최소 비용을 구하는 메소드를 만들어야 한다.

처음에는 DFS로 완전탐색을 구현했다가 시간초과에 걸리고 말았다.

그래서 시도한 것이 다익스트라(Dijkstra) 알고리즘.
다익스트라는 한마디로 '한 정점에서 다른 모든 정점으로 가는 최단 경로를 알려주는 알고리즘'이다.
다익스트라 메소드를 구현한 뒤, S, A, B 각각에 대해 수행하였다.

class Solution {
    
    static final int maxFee = 100_000;
    
    public int solution(int n, int s, int a, int b, int[][] fares) {
        final int[][] graph = new int[n+1][n+1];
        final int maxTotalFee = maxFee*(n-1);
        int answer = maxTotalFee*3;
        
        for(int[] tmp : fares)
            graph[tmp[0]][tmp[1]] = graph[tmp[1]][tmp[0]] = tmp[2];
        
        int[][] distance = new int[3][n+1];

        dijkstra(s, n, maxTotalFee, graph, distance[0]);
        dijkstra(a, n, maxTotalFee, graph, distance[1]);
        dijkstra(b, n, maxTotalFee, graph, distance[2]);
        
        for(int i = 1 ; i <= n ; i++)
            answer = Math.min(answer, distance[0][i] + distance[1][i] + distance[2][i]);
        
        return answer;
    }
    
    public void dijkstra(int x, int n, int maxTotalFee, int[][] graph, int[] distance){
        boolean[] check = new boolean[n+1];
        
        for(int i = 1 ; i <= n ; i++)
            distance[i] = maxTotalFee;
        
        check[x] = true;
        distance[x] = 0;
        
        for(int i = 1 ; i <= n ; i++)
            if(graph[x][i] > 0) distance[i] = graph[x][i];

        int minTotalFee;
        int minIndex;
        
        do {
            minTotalFee = maxTotalFee+1;
            minIndex = -1;
            for(int i = 1 ; i <= n ; i++){
                if(!check[i] && distance[i] < minTotalFee){
                    minTotalFee = distance[i];
                    minIndex = i;
                }
            }
            if(minIndex >= 0){
                check[minIndex] = true;
                for(int i = 1 ; i <= n ; i++){
                    if(!check[i] && graph[minIndex][i] > 0)
                        distance[i] = Math.min(distance[i], minTotalFee + graph[minIndex][i]);
                }
            }
        } while (minTotalFee <= maxTotalFee);
    }
}

.
.

모든 정점 사이의 최단거리를 구하는 '플루이드 와샬(Floyd Warshall)' 알고리즘도 이 문제에 적용 가능하다고 한다.
언젠가 이 알고리즘을 적용한 문제도 소개할 수 있기를.